Welcome to our page dedicated to area and volume problems! Here you will find a collection of challenging mathematical problems related to the measurement of areas and volumes.
First of all, we must know that area is a measure that describes the extension of a two-dimensional surface. It represents the amount of space occupied by a figure in a plane and is expressed in square units, such as square feet (ft²) or square inches (in²).
On the other hand, volume is a measure that describes the amount of three-dimensional space occupied by an object. It represents the space enclosed within a figure or a solid and is expressed in cubic units, such as cubic feet (ft³) or cubic inches (in³). Of course, area and volume vary according to the object.
These quantities are fundamental in many disciplines, from architecture and engineering to physics and geometry. Here, we will provide you with clear and step-by-step explanations of how to calculate the area and volume of different shapes and solids that appear in mathematical and/or everyday life problems.
Let's go! Get ready to develop your problem-solving skills. Enjoy and learn from the techniques we have developed for you.
Calculate the volume, in cubic centimeters, of a room that is  m (16.4 ft) long,
m (16.4 ft) long,  m (13.1 ft) wide and
m (13.1 ft) wide and  m (8.2 ft) high
m (8.2 ft) high
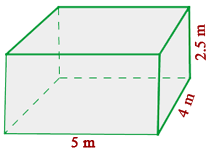
1 We calculate the volume
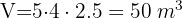
Knowing that 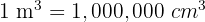 , we convert:
, we convert:
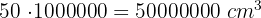
A pool is  m (26.2 ft) long,
m (26.2 ft) long,  m (19.7 ft) wide and
m (19.7 ft) wide and  m (4.9 ft) deep. The pool is painted at a rate of $
m (4.9 ft) deep. The pool is painted at a rate of $ per square meter
per square meter
A How much will it cost to paint it.
B How many liters of water will be needed to fill it.

1 We calculate the area to paint

2 We calculate the cost
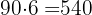
3 The liters needed to fill it is the volume of the pool multiplied by 1000
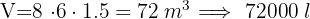
In a warehouse with dimensions  m (16.4 ft) long,
m (16.4 ft) long,  m (9.8 ft) wide and
m (9.8 ft) wide and  m (6.6 ft) high, we want to store boxes with dimensions
m (6.6 ft) high, we want to store boxes with dimensions  dm (3.3 ft) long,
dm (3.3 ft) long,  dm (2.0 ft) wide and
dm (2.0 ft) wide and  dm (1.3 ft) high. How many boxes can we store?
dm (1.3 ft) high. How many boxes can we store?

1 First we observe that
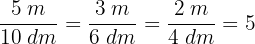
2 We calculate the volume of the warehouse

3 We calculate the volume of the boxes
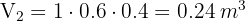
4 The number of boxes is obtained by dividing the warehouse volume by the volume of one box
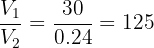 boxes
boxes
Determine the total area of a tetrahedron, an octahedron and an icosahedron with  cm (2.0 in) edge
cm (2.0 in) edge
1 The total area of a tetrahedron is
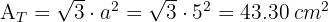
2 The total area of an octahedron is
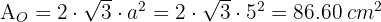
3 The total area of an icosahedron is
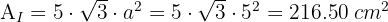
Calculate the height of a prism that has a base area of  dm² (1.29 ft²) and
dm² (1.29 ft²) and  l (12.7 gal) capacity
l (12.7 gal) capacity
1 We have that 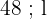 is equivalent to
is equivalent to 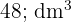 of volume
of volume
2 We calculate the volume of the prism

3 We equate both volumes

Calculate the amount of tin that will be needed to make  cylindrical cans with
cylindrical cans with  cm (3.9 in) diameter and
cm (3.9 in) diameter and  cm (7.9 in) height
cm (7.9 in) height
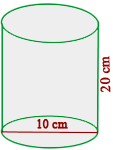
1 We calculate the total area of one can
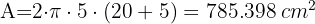
2 The amount used for 10 cans is
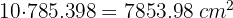
A cylinder has a height equal to the circumference of the base. And the height measures 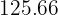 cm (49.5 in). Calculate:
cm (49.5 in). Calculate:
A Total area.
B Volume.
1 We calculate the radius
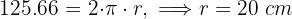
2 We calculate the total area

3 We calculate the volume
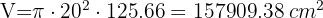
In a test tube with  cm (2.4 in) radius, four ice cubes with
cm (2.4 in) radius, four ice cubes with  cm (1.6 in) edge are placed. What height will the water reach when they melt?
cm (1.6 in) edge are placed. What height will the water reach when they melt?
1 We calculate the volume of the ice cubes
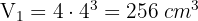
2 The test tube is cylindrical, so its volume is

3 We equate the volumes and obtain
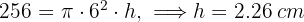
The dome of a cathedral has a hemispherical shape, with radius  m (164 ft). If restoring it costs $
m (164 ft). If restoring it costs $ per m², how much will the restoration budget amount to?
per m², how much will the restoration budget amount to?
1 We calculate the area of the hemisphere
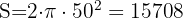
2 The restoration cost is
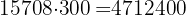
How many square tiles with  cm (7.9 in) sides are needed to cover the faces of a pool
cm (7.9 in) sides are needed to cover the faces of a pool  m (32.8 ft) long by
m (32.8 ft) long by  m (19.7 ft) wide and
m (19.7 ft) wide and  m (9.8 ft) deep?
m (9.8 ft) deep?

1 We calculate the area to cover
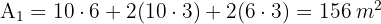
2 We calculate the area of one tile
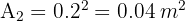
3 The number of tiles required is
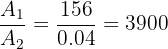
A cylindrical container with  cm (3.9 in) radius and
cm (3.9 in) radius and  cm (2.0 in) height is filled with water. If the mass of the full container is
cm (2.0 in) height is filled with water. If the mass of the full container is  kg (4.4 lb), what is the mass of the empty container?
kg (4.4 lb), what is the mass of the empty container?
1 We calculate the volume

2 The weight of the container is

For a party, Louis has made  cone-shaped hats with cardboard. How much cardboard will he have used if the hat dimensions are
cone-shaped hats with cardboard. How much cardboard will he have used if the hat dimensions are  cm (5.9 in) radius and
cm (5.9 in) radius and  cm (9.8 in) slant height?
cm (9.8 in) slant height?
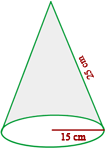
1 We calculate the area of one cone

2 The area required for 10 cones is
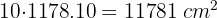
A cube with  cm (7.9 in) edge is full of water. Would this water fit in a sphere with
cm (7.9 in) edge is full of water. Would this water fit in a sphere with  cm (7.9 in) radius?
cm (7.9 in) radius?
1 We calculate the volume of the cube
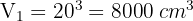
2 We calculate the volume of the sphere

Since the volume of the sphere is greater than the volume of the cube, we conclude that the water does fit in the sphere.
Calculate the diagonal of a rectangular prism  cm (3.9 in) long,
cm (3.9 in) long,  cm (1.6 in) wide and
cm (1.6 in) wide and  cm (2.0 in) high
cm (2.0 in) high
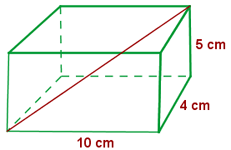
1 The diagonal is given by
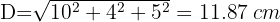
A sphere and a cube are filled with water at the same time at a rate of 1m³ per minute. If the sphere has a radius of  meters (16.4 ft) and the cube edge measures
meters (16.4 ft) and the cube edge measures  meters (26.2 ft), which will fill first?
meters (26.2 ft), which will fill first?
To solve this problem we must calculate the volume of each container. The formula for the volume of a sphere is

If 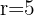 , then the volume of the sphere is
, then the volume of the sphere is
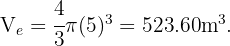
Similarly, the volume of a cube with edge  is given by
is given by
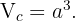
Thus, if  , then the volume of the cube is
, then the volume of the cube is

Since both containers are filled at the same rate of 1m³ per minute, then the sphere will fill in approximately 524 minutes or in 8 hours and 44 minutes. Similarly, the cube will fill in 512 minutes or in 8 hours and 32 minutes. Therefore the cube will fill with water first.
Remember that you can also find private math classes through our platform if you need additional support.


