The binomial distribution is one of the most important models in statistics and is used to describe phenomena where there are two possible outcomes in each trial, such as success or failure. This distribution is especially useful in situations where independent experiments are repeated, such as coin flipping or examining the effectiveness of a medical treatment. In this context, solved binomial distribution exercises allow us to illustrate how to calculate probabilities and other key parameters, such as mean and variance, in practical situations. Through these examples, we seek to facilitate understanding of the fundamental principles of binomial distribution and its application in solving statistical problems.
A berry distributor observes that out of every ten strawberries, one is not in excellent condition. What is the probability that out of 15 strawberries, none are in poor condition?
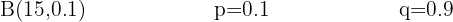
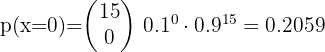
A person has a 0.7 probability of correctly answering a question. What is the probability that out of 10 questions, they answer all of them correctly?
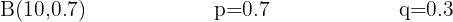
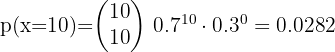
A die is rolled twice. What is the probability of obtaining two even numbers?
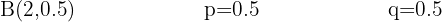
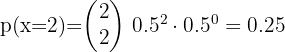
A soccer player scores a goal out of every 9 shots at the opposing goal. If he takes 15 shots at the rival team's goal, what is the probability that he scores two goals?
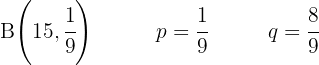
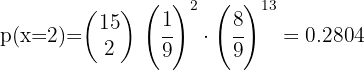
A basketball player makes 5 out of every 8 shots at the basket. If in a game he shoots 10 times at the hoop, what is the probability of making the shot on 6 occasions?
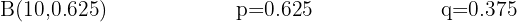
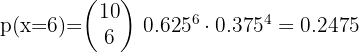
A farmer observes that out of every 10 plants, one gets sick. What is the probability that out of 12 plants, 2 get sick?
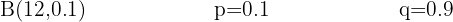
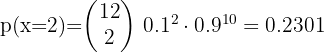
An author's latest novel has been a great success, to the point that 80% of readers have already read it. A group of 4 friends are reading enthusiasts:
1 What is the probability that 2 people in the group have read the novel?
2 What about at most 2?
1


2

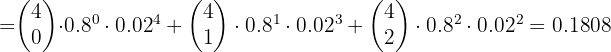
An insurance agent sells policies to five people of the same age who enjoy good health. According to current tables, the probability that a person under these conditions lives 30 years or more is 2/3. Find the probability that, after 30 years have passed, there are alive:
1 All five people
2 At least three people
3 Exactly two people
1
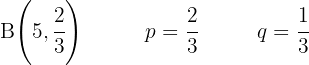
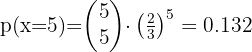
2
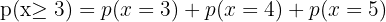
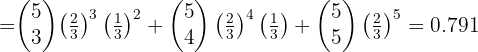
3
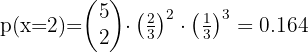
A coin is flipped four times. Calculate the probability that more heads than tails come up.
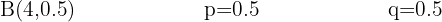
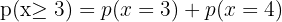
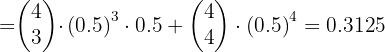
If from six to seven in the evening it is assumed that one out of every five telephone numbers is busy. What is the probability that, when 10 randomly chosen telephone numbers are dialed, only two are busy?

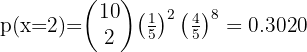
The probability that a man hits the target is 1/4. If he shoots 10 times
1 What is the probability that he hits exactly three times?
2 What is the probability that he hits at least once?
1

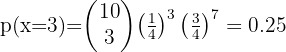
2
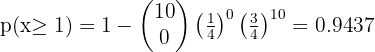
In breathalyzer tests it has been observed that 5% of controlled drivers test positive and that 10% of controlled drivers are not wearing their seatbelt. It has also been observed that the two infractions are independent. A traffic officer stops five drivers at random. Taking into account that the number of drivers is sufficiently large to estimate that the proportion of offenders does not vary when making the selection.
1 Determine the probability that exactly three drivers have committed one of the two infractions.
2 Determine the probability that at least one of the controlled drivers has committed one of the two infractions.
1
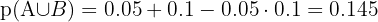


2
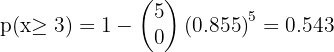
The probability that an item produced by a factory is defective is p = 0.02. A shipment of 10,000 items was sent to some warehouses. Find the expected number of defective items, the variance and the standard deviation.
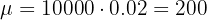

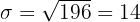
In a container there are 30 balls, 10 red and the rest white. A ball is chosen at random and it is noted if it is red; the process is repeated, returning the ball, 10 times. Calculate the mean and standard deviation.
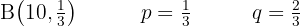
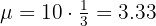

A laboratory claims that a drug causes side effects in a proportion of 3 out of every 100 patients. To test this claim, another laboratory randomly chooses 5 patients to whom it applies the drug. What is the probability of the following events?
1 No patient has side effects
2 At least two have side effects
3 What is the average number of patients that the laboratory expects to suffer side effects if it chooses 100 patients at random?
1

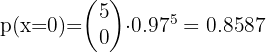
2
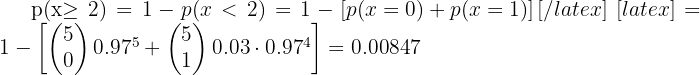
3
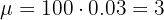
If you're prefer a math teacher, don't hesitate to check out our instructors. You can find both in-person and online lessons, and there's an teacher for every need!


