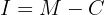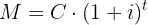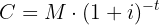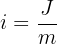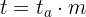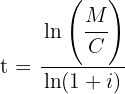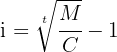Chapters

What Is Interest and How Is It Calculated?
In some banks, savings accounts or even in loans and pawns we can observe that a monthly interest is charged. This does not mean that all interests must be like this.
The period is the time in which interest is applied, this can be annual, monthly, weekly, or even daily.
For the case of the exercises proposed in this section, we will be working with annual interest.
Also, there is simple interest and compound interest. The exercises we will see deal with compound interest.
Formulas for Calculating Compound Interest
For the following formulas we have the following notation:
 : Interest
: Interest : Initial capital
: Initial capital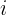 : Interest rate
: Interest rate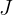 : Nominal interest rate
: Nominal interest rate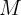 : Amount (or future value)
: Amount (or future value)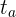 : Time of loan or investment
: Time of loan or investment : Period of loan or investment
: Period of loan or investment : Capitalization frequency
: Capitalization frequency
Thus, the formulas related to compound interest calculation, when the interest rate and time use the same time unit, are:
Note that if time and interest use different units, then we will have to make the appropriate conversions before using the formulas.
Proposed Interest Calculation Exercises
For how long must a capital of $25,000 be invested at 5% quarterly so that with compound interest it becomes $30,387.66?
Note that we have the amount or final capital, the initial capital and the interest rate
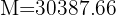
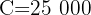
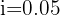 quarterly
quarterly
We directly apply the formula to calculate time, this will be in quarters since the interest rate is quarterly:
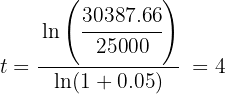
Therefore, the required time is 4 quarters.
$45,000 is lent with compound interest and after 2 years $52,488 is received. Calculate the interest rate.
Note that we have the capital, the amount and the investment period
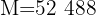
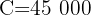
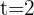 years
years
We directly apply the formula to calculate the interest rate
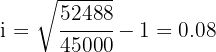
Thus, the interest rate is 8% annually.
Find the compound interest rate (as a percentage) at which a capital should be lent so that after 20 years the interest is equivalent to the lent capital.
We want the interest to equal the capital, so the amount equals twice the capital
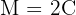
Note that we have amount, capital and the investment period
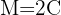

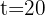
Since the capital is different from 0, we cancel 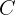 from both sides of the interest rate equation and substitute the investment period:
from both sides of the interest rate equation and substitute the investment period:
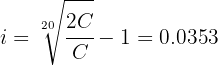
Thus, the interest rate is 3.53% annually.
In how much time will the compound interest equal triple the initial capital placed at an interest rate of 6%?
We want the interest to be triple the capital, so the amount equals four times the capital
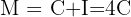
Note that we have amount, capital and interest rate
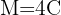

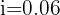
Since the capital is different from 0, we cancel 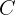 in the equation to calculate time
in the equation to calculate time
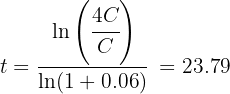
Therefore, the required time is 23.79 years.
Find the compound interest produced during five years, by a capital of $30,000, at 6%.
Note that we have the investment period, capital and interest rate
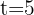
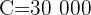
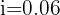
Here we need to find the value  . Since we already have all the necessary data, we will only use the formula to calculate it:
. Since we already have all the necessary data, we will only use the formula to calculate it:
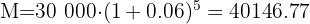
Thus, the compound interest would be 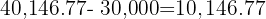 after five years.
after five years.
Calculate the final capital after six months, given an initial capital of $10,000 and a compound interest rate of 3.5% monthly
Note that we have the investment period, capital and interest rate
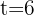
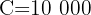
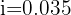
To solve this exercise we substitute directly into the formula to calculate the amount
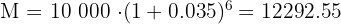
Therefore, the capital is $12,292.55 after 6 months.
Find the nominal interest rate of an investment of $30,000 that after five years at an interest rate compounded quarterly becomes $50,000.
Note that we have the investment time, capital and amount
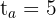
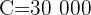

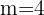
We calculate the investment period
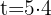
Here we need to find the value  . Since we already have all the necessary data, we will only use the formula to calculate it:
. Since we already have all the necessary data, we will only use the formula to calculate it:
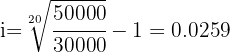
Substituting the values 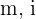 in the nominal interest rate formula we have
in the nominal interest rate formula we have
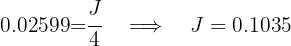
Therefore, the nominal interest rate is 10.35%.
In how much time will a capital of $30,000 produce an amount of $40,000 with a compound interest rate of 4%?
Note that we have amount, capital and interest rate
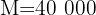
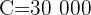
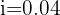
We substitute the data into the equation to calculate time
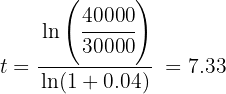
Therefore, the required time is 7.33 years.