As you may know, there are two main ways to solve derivatives. The first is by using the limit definition:
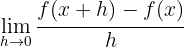
And the second is by applying standard formulas for different types of functions. In these exercises, we’ll use the second method.
Calculate the derivatives of the following functions:
1 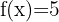
2 
3 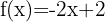
4 
5 
6 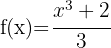
7 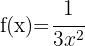
8 
9 
1. 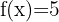
In this case, we use the formula 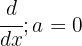 , which means the derivative of any constant is always zero.
, which means the derivative of any constant is always zero.

2. 
Here, we use the formula 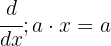 , which means that when a constant multiplies a variable, the derivative is the constant.
, which means that when a constant multiplies a variable, the derivative is the constant.

3. 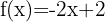
In this case, we apply the rule 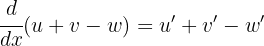 , which tells us that for the sum or difference of functions (or algebraic terms), the derivative is the sum and/or difference of their individual derivatives.
, which tells us that for the sum or difference of functions (or algebraic terms), the derivative is the sum and/or difference of their individual derivatives.

4. 
We differentiate each algebraic term. For the first one, we use the formula 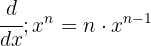 .
.

5. 
We differentiate each algebraic term.
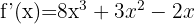
6. 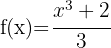
In this case, we can rewrite the function as:
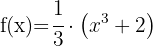
Therefore, the derivative will be  multiplied by the derivative of the function
multiplied by the derivative of the function 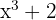
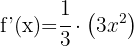

7. 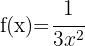
For this type of function, where the variable is in the denominator, we can apply the rule of exponents:
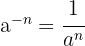
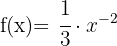
To differentiate, we apply the formula 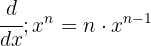
So we get:
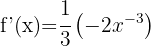

8. 
To differentiate a quotient, we use the formula:

Therefore, the derivative is:
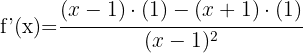

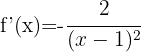
9. 
To differentiate a product, we use the formula:

Therefore, the derivative becomes:
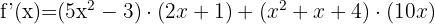
Use the power rule to calculate derivatives:
1 
2 
3 
4 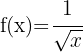
5 
6 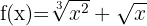
7 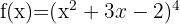
Remember, the formula to differentiate a power is:
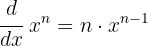
This formula will be used throughout the exercises in this section.
1 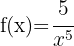
Using exponent rules, we can rewrite the function as:

Applying the power rule:
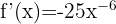
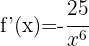
2 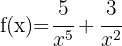
Using exponent rules, we can rewrite the function as:

Applying the power rule:
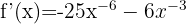

3 
Using exponent rules, we can rewrite the function as:
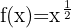
Applying the power rule:


4 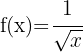
Using exponent rules, we can rewrite the function as:

Applying the power rule:
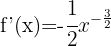
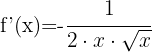
5 
Using exponent rules, we can rewrite the function as:
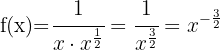
Applying the power rule:
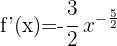
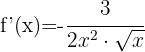
6 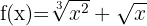
Using exponent rules, we can rewrite the function as:
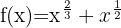
Applying the power rule:
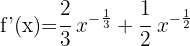
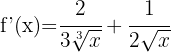
7 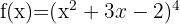
In this case, we have a function raised to a power, so we can apply the rule:
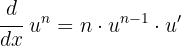

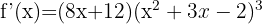
Differentiate exponential functions:
1 
2 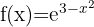
3 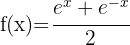
4 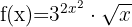
5 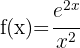
In this section, we will use the following formulas:

1 
We apply the first formula and get:
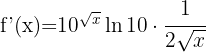
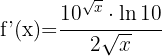
2 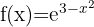
We apply the second formula and get:


3 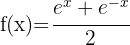
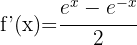
4 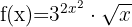
We start by applying the product rule: 

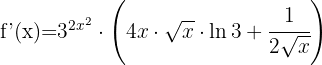
5 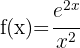
We begin by applying the quotient rule: 
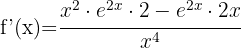
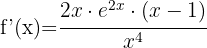

Calculate the derivative of logarithmic functions:
1 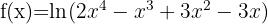
2 
3 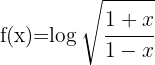
4 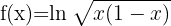
5 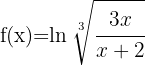
In this section, we’ll use the following formulas:
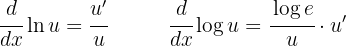
Additionally, we can apply logarithmic properties to rewrite the function in a simpler form before differentiating
1 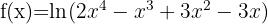
We apply the formula to differentiate natural logarithms
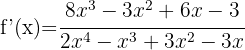
2 
Using the logarithmic identity 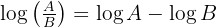 , we get:
, we get:

We differentiate each term using the formula for natural logarithms
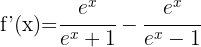
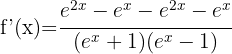
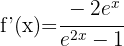
3 
Using the logarithmic identities 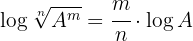 and
and 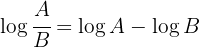 , we get:
, we get:

We apply the logarithmic derivative formula


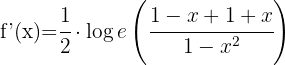
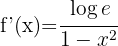
4 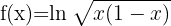
Using the properties 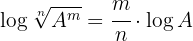 and
and 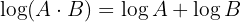 , we get:
, we get:
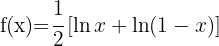
We apply the formula to differentiate natural logarithms.
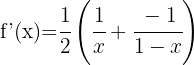
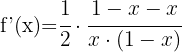
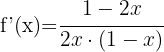
5 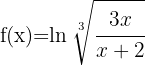
Using the properties 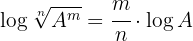 and
and 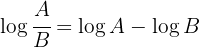 , we get:
, we get:

We apply the formula to differentiate natural logarithms.

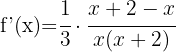

Use the formula for the derivative of a root
1 
2 
3 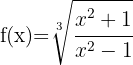
To differentiate functions that include roots, we can rewrite them as exponents (as in the previous section), or we can use the following root derivative formulas:
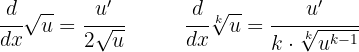
1 
Since it's a square root, we use the first formula.
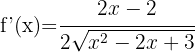
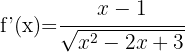
2 
Since it's a fourth root, we use the second formula.

3 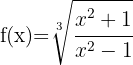
Since it's a cube root, we start by applying the second formula. The expression inside the root is a quotient, so we apply the quotient rule. 
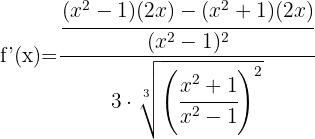
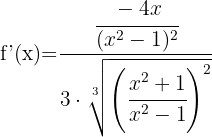
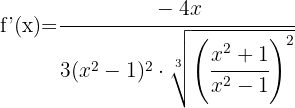
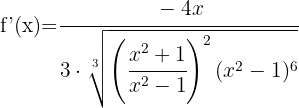
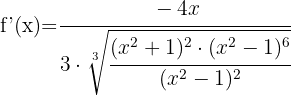
We simplify the 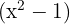 expression by cancelling it from both the numerator and denominator, and we get:
expression by cancelling it from both the numerator and denominator, and we get:
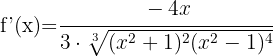

Use the formula for the derivative of sine
1 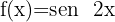
2 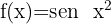
3 
To differentiate functions involving sine, we use the following formula:
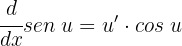
1 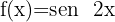
We identify the angle 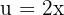 and compute its derivative.
and compute its derivative.
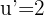
Then we apply the formula for the derivative of sine.

2 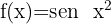
We identify the angle  and compute its derivative.
and compute its derivative.
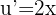
Then we apply the formula for the derivative of sine.
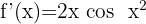
3 
We identify the angle 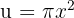 and compute its derivative.
and compute its derivative.
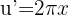
Then we apply the formula for the derivative of sine.
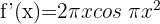
Use the formula for the derivative of cosine
1 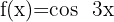
2 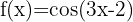
3 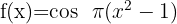
To differentiate functions involving cosine, we use the following formula:
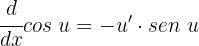
1 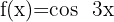
We identify the angle 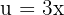 and compute its derivative.
and compute its derivative.
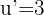
Then we apply the formula for the derivative of cosine.
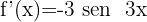
2 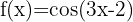
We identify the angle 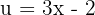 and compute its derivative.
and compute its derivative.
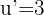
Then we apply the formula for the derivative of cosine.
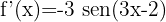
3 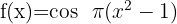
We identify the angle 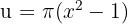 and compute its derivative.
and compute its derivative.
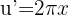
Then we apply the formula for the derivative of cosine.
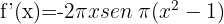
Use the formula for the derivative of tangent
1 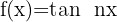
2 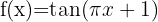
3 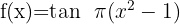
To differentiate functions involving tangent, we use the following formula:
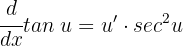
1 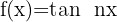
We identify the angle 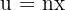 and compute its derivative.
and compute its derivative.
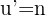
Then we apply the formula for the derivative of tangent.
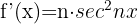
2 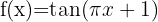
We identify the angle 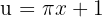 and compute its derivative.
and compute its derivative.
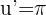
Then we apply the formula for the derivative of tangent.
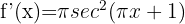
3 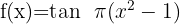
We identify the angle 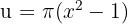 and compute its derivative.
and compute its derivative.
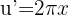
Then we apply the formula for the derivative of tangent.
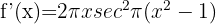
Use the chain rule to differentiate the following exponential functions
1 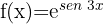
2 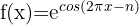
To differentiate functions involving exponentials, we use the following formula:
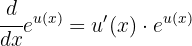
1 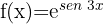
We identify the angle 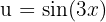 and compute its derivative.
and compute its derivative.
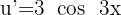
Then we apply the formula for the derivative of the exponential function.
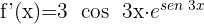
2 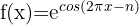
We identify the angle 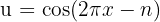 and compute its derivative.
and compute its derivative.

Then we apply the formula for the derivative of the exponential function.
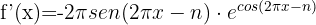
Use the chain rule to differentiate the following natural logarithmic functions
1 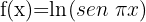
2 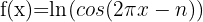
To differentiate functions involving natural logarithms, we use the following formula:
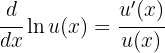
1 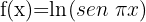
We identify the angle 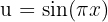 and compute its derivative.
and compute its derivative.

Then we apply the formula for the derivative of the natural logarithm.
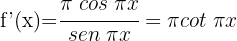
2 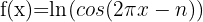
We identify the angle 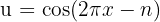 and compute its derivative.
and compute its derivative.

Then we apply the formula for the derivative of the natural logarithm.
Still finding derivatives hard to grasp, even after reading our explanations?
Find a private math tutor who can adapt to your level and help you understand step by step.


