Chapters

Table of the Most Common Derivatives
Basic Derivatives
Exponential and Logarithmic Derivatives
Trigonometric Derivatives
Inverse Trigonometric Derivatives
Chain Rule
Implicit Derivative Formula

The derivative table was introduced by Charles Goodheart at the London School of Economics in 1947 and it contains the four components of a derivative: direction, property, time and rate. A derivative is a term that refers to a relationship between two or more variables. One of the most important concepts about derivatives is that they are equal when expressed in terms of some other constant. It is also possible to determine the derivatives of a function, but this can be very difficult because functions often have complex boundary conditions.

A derivative table helps determine the value of a given quantity by determining what effect the input variable has on the output variable. In many cases, a derivative calculation will help you predict the behavior of a given equation or integral. For many investors it is necessary to stay aware of changes in the stock market, so they may choose to use the derivative table as a tool to determine the value of stocks for example.

A derivative table can also be used to plot a trend line, since it can plot a line for any variable that is correlated with time. The temporal correlation between two variables is the same for each time step, making it easier to plot a trend line.

The best Mathematics tutors available

Table of the Most Common Derivatives

Below is a table with some of the most common functions presented in textbooks and their derivative:

Simple Function	Derivative
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$
$\text{[math]}$	$\text{[math]}$

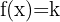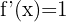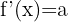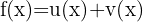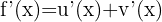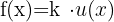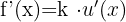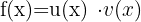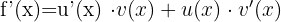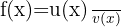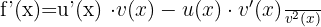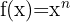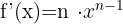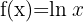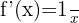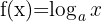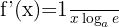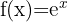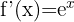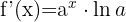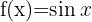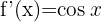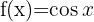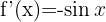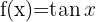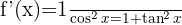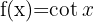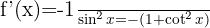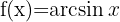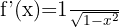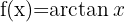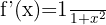Additionally, in the following sections the derivative formulas are classified:

Basic Derivatives

Derivative of a Constant

$\text{[math]}$

Derivative of x

$\text{[math]}$

Derivative of Linear Function

$\text{[math]}$

Derivative of a Power

$\text{[math]}$

Derivative of a Root

$\text{[math]}$

Derivative of a Square Root

$\text{[math]}$

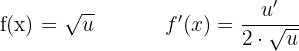
Derivative of a Sum

$\text{[math]}$

Derivative of a Constant Times a Function

$\text{[math]}$

Derivative of a Product

$\text{[math]}$

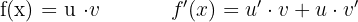
Derivative of Constant Divided by a Function

$\text{[math]}$

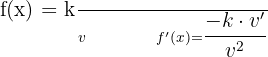
Derivative of a Quotient

$\text{[math]}$

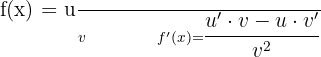
Exponential and Logarithmic Derivatives

Derivative of Exponential Function

$\text{[math]}$

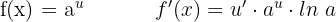
Derivative of Exponential Function with Base E

$\text{[math]}$

Derivative of a Logarithm

$\text{[math]}$

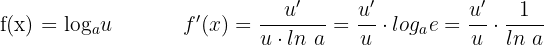
Derivative of Natural Logarithm

$\text{[math]}$

Trigonometric Derivatives

Derivative of Sine

$\text{[math]}$

Derivative of Cosine

$\text{[math]}$

Derivative of Tangent

$\text{[math]}$

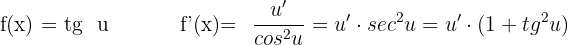
Derivative of Cotangent

$\text{[math]}$

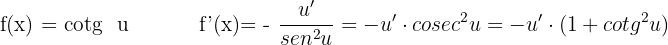
Derivative of Secant

$\text{[math]}$

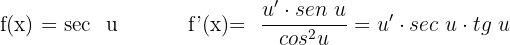
Derivative of Cosecant

$\text{[math]}$

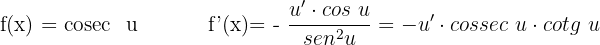
Inverse Trigonometric Derivatives

Derivative of Arcsine

$\text{[math]}$

Derivative of arccosine

$\text{[math]}$

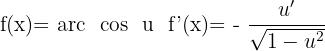
Derivative of Arctangent

$\text{[math]}$

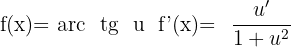
Derivative of Arccotangent

$\text{[math]}$

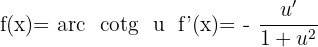
Derivative of Arcsecant

$\text{[math]}$

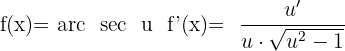
Derivative of Arccosecant

$\text{[math]}$

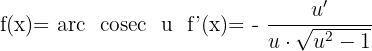
Derivative of Power-Exponential Function

$\text{[math]}$

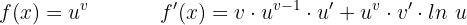
Chain Rule

$\text{[math]}$

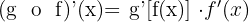
Implicit Derivative Formula

$\text{[math]}$

Did you like this article? Rate it!

5.00 (2 Note(n))

Agostina Babbo

Agostina Babbo is an English and Italian to Spanish translator and writer, specializing in product localization, legal content for tech, and team sports—particularly handball and e-sports. With a degree in Public Translation from the University of Buenos Aires and a Master's in Translation and New Technologies from ISTRAD/Universidad de Madrid, she brings both linguistic expertise and technical insight to her work.

Essential Derivative Formulas and Rules

Table of the Most Common Derivatives