Chapters
Calculating the distance between two points is an essential tool in various fields, from geometry to navigation and data science. It allows us to measure the separation between two locations in a space, whether in a two-dimensional plane or in three-dimensional space. This notion of distance is not only fundamental in mathematics, but also has practical applications in the real world, such as calculating the distance between cities on a map, determining the proximity between objects in three-dimensional space, or even evaluating similarities between data sets.
Whether you dive into the world of Cartesian coordinates in the plane or explore dimensions beyond, calculating the distance between two points will provide you with a solid foundation for understanding spatial relationships and applying your knowledge in a variety of disciplines. Let's start measuring distances and exploring the importance of this fundamental concept!
Distance Between Two Points
To study the distance between two points, let's consider the following figure:
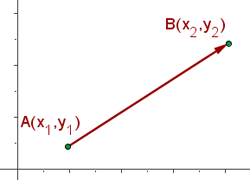
In the figure we can find two points 
and 
in the Cartesian plane connected by a vector. The magnitude of the vector colored in red that connects the points is the value that represents the distance between points and .
The Formula for Calculating the Distance Between Two Points and the Pythagorean Theorem
The formula for calculating this magnitude is given by the following expression:
The value of this formula can be obtained using the Pythagorean Theorem. To do this, let's consider the right triangle with vertices
, and 
.
Notice that the value of the hypotenuse of this triangle is the distance between points
and .
Since the magnitude of the segments that connect and , and are 
and 
respectively.
The Pythagorean Theorem states that the value of the hypotenuse or the distance between and is 
Examples of Distance Between Two Points
1 Calculate the distance between the points: 
and 
2 Determine the condition for points 
and 
to be one unit apart.
If the distance between 
and 
is one, this means that
Squaring both sides to eliminate the square root:
3 Prove that the points: 
, 
and 
belong to a circle with center 
.
If 
is the center of the circle, for 
and 
to belong to a circle, by definition the distances from to , to and to must be equal. Let's verify this using the distance formula between two points.
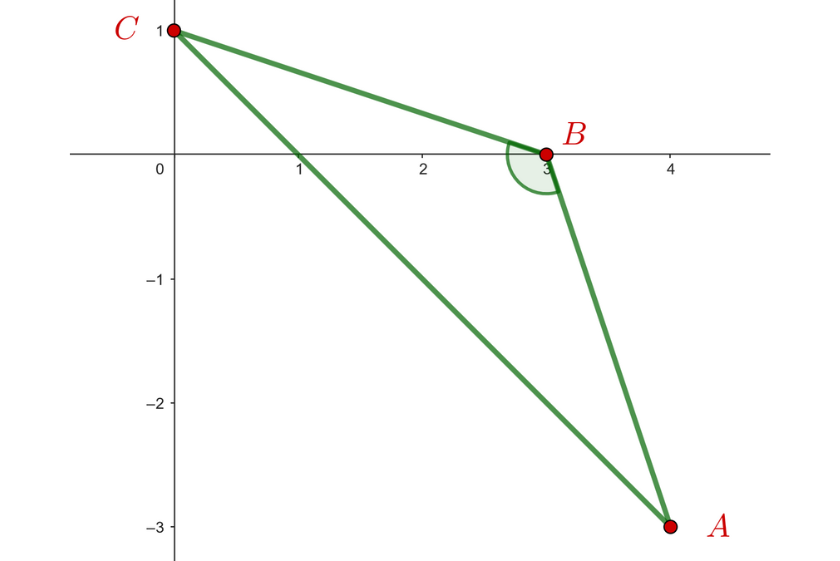
4 Classify the triangle determined by the points: 
, 
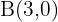and 
First let's calculate the distances between the triangle points to be able to classify its type.
Since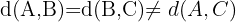 
, we can conclude that the triangle is not equilateral, because if it were, the distances between any of its points would be equal.
Furthermore, if:
then the triangle is acute-angled,
when 
the triangle is right-angled,
and finally, if 
then the triangle is obtuse-angled.
From the above it follows that:
And therefore, the triangle is obtuse-angled.
Did you like this article? Rate it!
Loading...
