Chapters
How Do We Find the Equation of the Line Knowing Two Points?
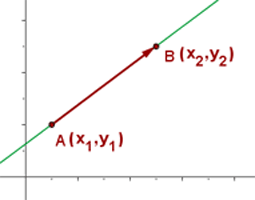
Let the points 
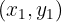and 
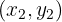determine a line 
.
A direction vector of the line is:
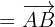
Whose components are: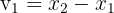 
and 
Substituting these values in the continuous form:
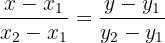
We can find the equation of the line.
Finding the Equation of the Line When Two Points Are Known
Find the equation of the line that passes through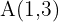 
and 
We substitute the values in the continuous form:
Therefore, the equation of the line is:
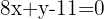
Knowing the Equation of the Line, Find Two Points on it
When we know the equation of a line it is very simple to find points that belong to it. Remember that the equation of the line can be written in different forms: general, parametric, or slope-intercept for example.
To find points on the line, it is most recommended to use the slope-intercept form and make a tabulation (table of values) where we find many coordinates (points) that belong to the line.
Example:
Let the general equation of the line be: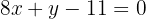 
We can write it in slope-intercept form (solving for y):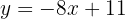 
Now we can assign any value to 
, and obtain the corresponding value for y as shown in the table below:
| Values we assign to x | Slope-intercept equation | Value obtained for y | Coordinate (point) that belongs to the line |
|---|---|---|---|
| x | y=-8x+11 | y | (x,y) |
| 2 | y=-8(2)+11 y=-16+11 y=-5 | -5 | (2,-5) |
| 0 | y=-8(0)+11 y=0+11 y=11 | 11 | (0,11) |
| -3 | y=-8(-3)+11 y=24+11 y=35 | 35 | (-3,35) |
Another simple way to quickly obtain 
points on the line is by remembering what each element of the slope-intercept equation means:
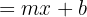
Where 
represents the slope of the line and 
represents the coordinate of the point where the line crosses the 
axis, that is, knowing this will quickly tell us that one point on the line is the coordinate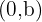 
.
Now, suppose in our equation the variable 
and, then we have 
.
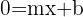We solve for :
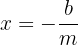
This value is known as 
and is the value where the line crosses the axis, knowing this will quickly tell us that one point on the line is the coordinate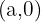 
Thus, in our equation that we used as an example, we would obtain the points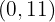 
and 
Did you like this article? Rate it!
Loading...
