Chapters
Welcome to our section dedicated to solving linear equations and their application in a wide variety of problems. Linear equations are the foundation of mathematics and have a wide range of applications in various fields, from physics to economics. In this guide, we will accompany you on a learning journey that encompasses both solving linear equations and their application in real-world situations.
Solving a linear equation involves finding the value or values of an unknown variable that make the equation true. It is a systematic process that involves careful algebraic manipulation. Additionally, we will learn to apply linear equations to solve practical problems in various disciplines.
It is essential to remember that knowledge and application of linear equations are essential skills in mathematics and in solving everyday problems. Throughout this guide, we will explore exercises that will help us understand how to use this mathematical tool to analyze and solve situations we may encounter in our daily lives.
Equation Exercises
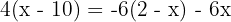
1. We perform the multiplications on both sides of the equation:
2. We add and subtract like terms on both sides of the equation:
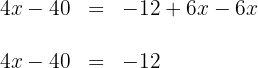
3. To solve for 
, first we add 
to both sides of the equation and simplify:
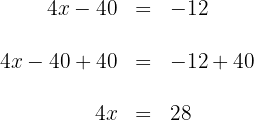
4. To obtain , now we multiply by 
on both sides of the equation and simplify:
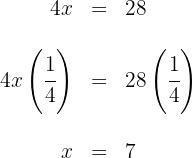
Thus,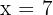 
is the solution of the equation.
1. We perform the multiplications:
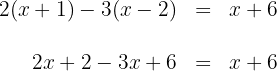
2. We add and subtract like terms on both sides of the equation:
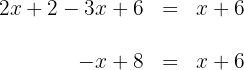
3. To solve for , first we subtract and 
from both sides of the equation and simplify:
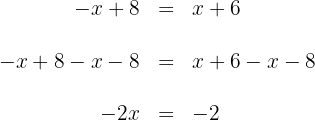
4. To obtain , now we multiply by 
on both sides of the equation and simplify:
Thus, 
is the solution of the equation.
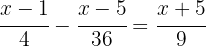
1. We calculate the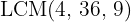 
:
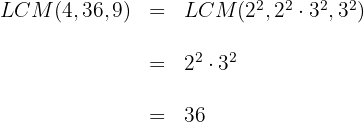
2. We multiply both sides of the equation by :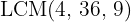
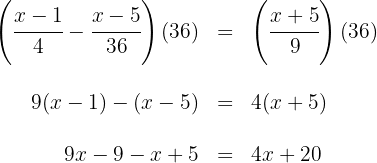
3. We add and subtract like terms on both sides of the equation:
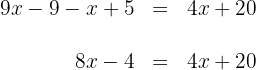
4. To solve for , first we subtract 
and add 
to both sides of the equation and simplify:
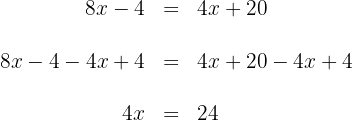
5. To obtain , now we multiply by on both sides of the equation and simplify:
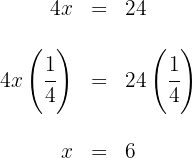
Thus, 
is the solution of the equation.
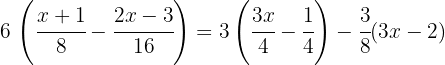
1. We perform the multiplications and simplify the fractions:
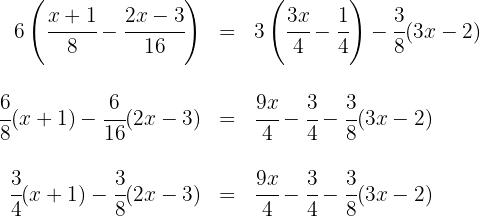
2. We calculate the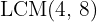 
of the denominators:
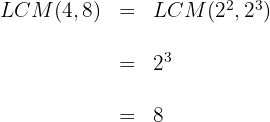
3. We multiply both sides of the equation by :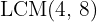
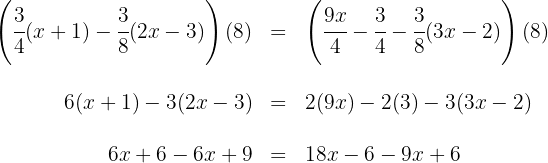
4. We add and subtract like terms on both sides of the equation:
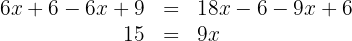
5. To solve for , we multiply on both sides of the equation and simplify:
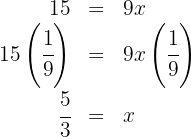
Thus,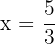 
is the solution of the equation.
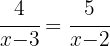
1. We multiply both sides of the equation by 
and and simplify:
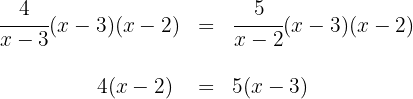
2. We perform the multiplications:
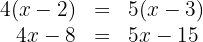
3. We subtract and add 
to both sides of the equation:
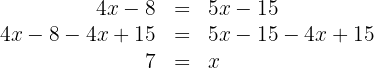
Thus, 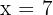is the solution of the equation.
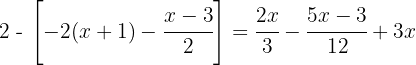
1. We remove the brackets:
2. We calculate the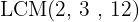 
of the denominators:
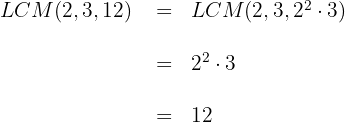
3. We multiply both sides of the equation by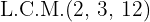 
:
4. We add and subtract like terms:
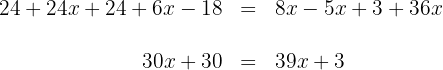
5. We subtract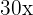 
and 
from both sides of the equation:
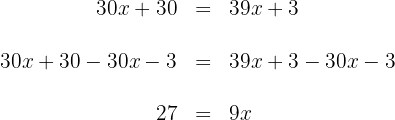
6. We multiply both sides of the equation by :
Thus, 
is the solution of the equation.
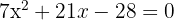
1. We solve using the quadratic formula to find the roots of the quadratic equation:
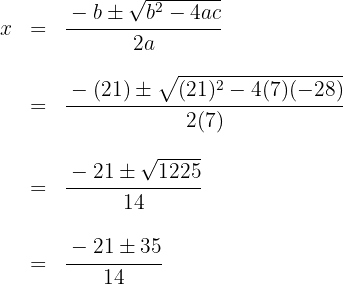
The roots are:
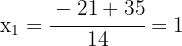
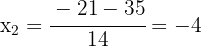
2. The roots of the equation are the solutions of the equation. Thus, the solutions are and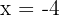 
.
1. We solve using the quadratic formula to find the roots of the quadratic equation:
Since square roots of negative numbers do not exist in the real numbers, we conclude that the equation has no real solutions.
1. We solve using the quadratic formula to find the roots of the quadratic equation:
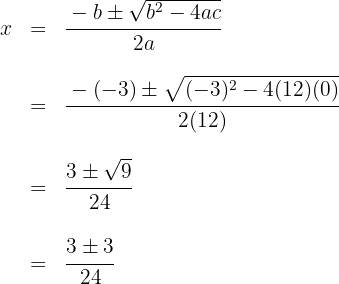
The roots are:
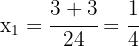
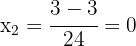
2. The roots of the equation are the solutions of the equation. Thus, the solutions are 
and 
.
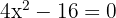
1. We solve using the quadratic formula to find the roots of the quadratic equation:
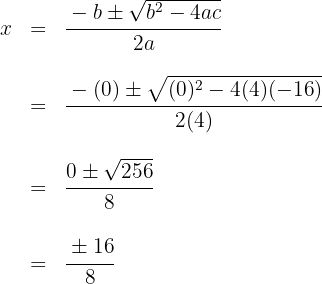
The roots are:
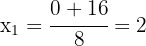
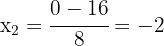
2. The roots of the equation are the solutions of the equation. Thus, the solutions are 
and 
.
Application Problems
A father is 35 years old and his son is 5. After how many years will the father's age be three times greater than his son's age?
1. The current age of the father is 35 and the son's is 5, while represents the years that must pass for the given condition to be met.
2. We write the given condition as an equation:
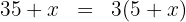
3. We perform the multiplication:
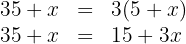
4. We subtract 
and 
from both sides of the equation:
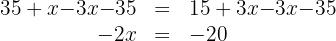
5. To solve for , we multiply both sides of the equation by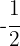 
and simplify:
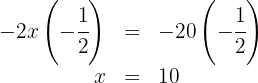
6. In 
years, the father's age will be three times greater than his son's.
If double a number minus half of it equals 54, what is the number?
1. Since we don't know the requested number, we represent it by .
2. We write the given condition as an equation:
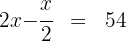
3. We multiply both sides of the equation by 2:
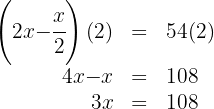
4. We multiply both sides of the equation by 
:
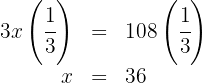
5. The number we're looking for is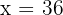 
.
The base of a rectangle is double its height. What are its dimensions if the perimeter measures 11.8 inches?
1. We represent the height by , so its base is 
.
2. We write the perimeter condition as an equation:
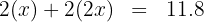
3. We perform the multiplications and add like terms:
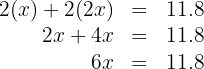
4. We multiply both sides of the equation by 
:
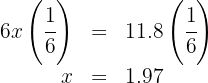
5. The height is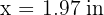 
and its base is 
.
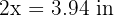At a gathering, there are twice as many women as men and triple the number of children as men and women together. How many men, women, and children are there if the gathering consists of 96 people?
1. We represent the number of men by , so the number of women is and the number of children is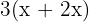 
.
2. We write the given condition as an equation:
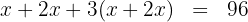
3. We perform the multiplications and add like terms:
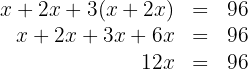
4. We multiply both sides of the equation by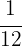 
:
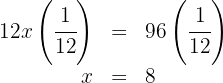
5. The number of men is 
, the number of women is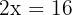 
, and the number of children is 
.
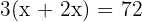We have consumed 
of a drum of oil. We replenish 10 gallons and the drum is filled to 
of its capacity. Calculate the capacity of the drum.
1. We call the capacity of the drum, and since we have consumed of its capacity, there remains:
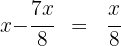
2. By replenishing 10 gallons, we write the second given condition as an equation:
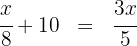
3. We multiply both sides of the equation by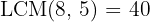 
:
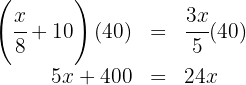
4. We subtract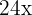 
and 
from both sides of the equation:
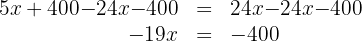
5. We multiply both sides of the equation by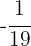 
:
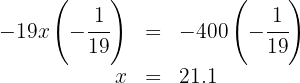
5. The capacity of the drum is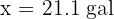 
.
A farm has pigs and turkeys; in total there are 35 heads and 116 legs. How many pigs and turkeys are there?
1. We call the number of pig heads, and since there are 35 heads in total, then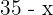 
is the number of turkey heads.
2. We write the condition for the legs, where pigs have 4 legs and turkeys have 2:
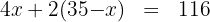
3. We multiply and then add like terms:
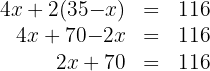
4. We subtract 
from both sides of the equation:
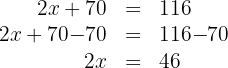
5. We multiply both sides of the equation by 
:
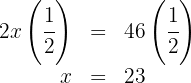
5. There are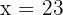 
pigs and 
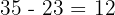turkeys.
Luis took a trip in his car, during which he consumed 5.3 gallons of gasoline. He made the trip in two stages: in the first, he consumed 
of the gasoline in the tank, and in the second stage, half of the remaining gasoline. Find the amount of gallons of gasoline in the tank and the gallons consumed in each stage.
1. We call the gallons of gasoline in the tank.
2. We write the condition for the first stage:
3. We write the condition for the second stage:
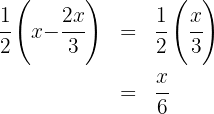
4. To find the amount of gasoline in the tank, we add what was consumed in both stages, which equals 5.3 gallons:
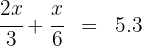
5. We multiply both sides of the equation by 
:
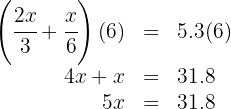
6. We multiply both sides of the equation by 
:
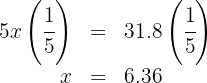
Thus, the tank had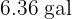 
.
In the first stage,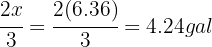 
was consumed, while in the second stage 
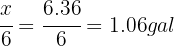was consumed.
In a bookstore, Ana buys a book with a third of her money and a comic with two-thirds of what she had left. Upon leaving the bookstore, she had $13.20. How much money did Ana have?
1. We call the total amount of money.
2. We write the condition for the book:
3. We write the condition for the comic:
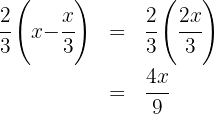
4. To find the amount of money she had, we add the expenses for the book and comic together with the leftover money:
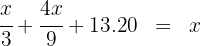
5. We multiply both sides of the equation by 
and add like terms:
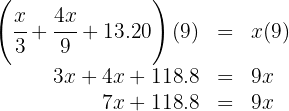
6. We subtract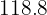 
and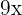 
from both sides of the equation:
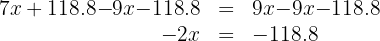
7. We multiply both sides of the equation by :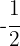
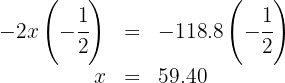
Thus, Ana had $59.40.
A truck leaves a city at a speed of 25 mph. One hour later, a car leaves the same city in the same direction at 37 mph. Find the time it will take for the car to catch up.
1. We call 
the time used by the truck, so the time used by the car is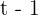 
.
2. Both vehicles travel the same distance, so:
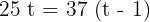
3. We perform the multiplication:
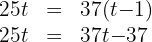
4. We subtract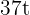 
from both sides of the equation:
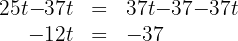
5. We multiply both sides of the equation by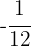 
:
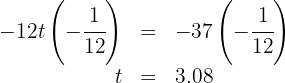
Thus, for the vehicles to meet, the truck takes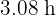 
while the car takes 
.
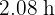The two digits of a number are consecutive. The larger is in the tens place and the smaller is in the units place. The number equals six times the sum of the digits. What is the number?
1. We call the units digit; since they are consecutive, the tens digit is 
.
2. If we have a two-digit number, for example 
, we can decompose it as follows:
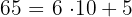
3. Our two-digit number is 
; with the given condition we obtain:
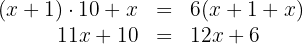
4. We subtract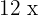 
and from both sides of the equation:
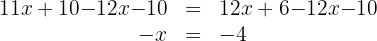
5. We multiply both sides of the equation by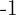 
and obtain 
.
Thus, the number we're looking for is:
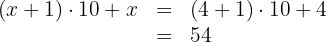
Suppose you are saving money to buy a new cell phone that costs $700. You have a part-time job and earn $50 per day worked. Additionally, you receive a weekly allowance of $20 from your parents. Suppose you spend $3 for each day you go to work. You want to know how many days per week you need to work to be able to buy the cell phone in a certain number of weeks. How many days per week do you need to work to buy the cell phone in 8 weeks?
Let be the number of days we work per week. Then, the net amount per week that we generate by working is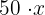 
dollars. Now, we see that we spend dollars weekly on transportation, and we earn $20 additional weekly. So, per week we generate:
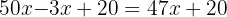
Then, in 8 weeks we generate:
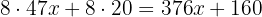
If in this period we need a minimum of $700, we obtain the following equation:
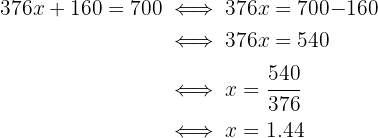
That is, if we work at least 1.44 days per week, we can buy the cell phone in 8 weeks.
A clothing store sells t-shirts at a fixed price of $15 each. Additionally, the store charges a shipping fee of $5 for each order placed. A customer wants to buy an unknown number of t-shirts and is willing to spend a maximum of $80 in total, including the price of the t-shirts and the shipping fee. How many t-shirts can the customer buy without exceeding their budget of $80?
Let be the number of t-shirts the customer can buy. Then, the equation to consider is:
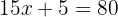
Then, we solve for the variable:
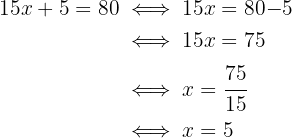
That is, the customer with a budget of $80 can only buy at most 5 t-shirts.
A student works during the summer to save money for school expenses. They earn $8 per hour worked and plan to work an unknown number of hours during vacation. Additionally, their school expenses amount to $600. The student wants to know how many hours they must work to cover their school expenses. How many hours do they need to work? If they are only allowed to work 6 hours daily, how many days must they work?
Let be the number of hours they must work. Then, the money earned can be calculated as follows:
Money Earned = (Money per hour) × (hours worked)
If we need $600, then we want the money earned to be 600, and we must solve for the hours worked:
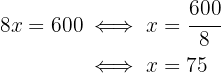
That is, they must work 75 hours to complete their goal. Now, if they can only work 6 hours daily, then they must work for:
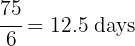
Since they must complete the workday, they must work for 13 complete days.
A shipping company offers two types of rates for shipping packages. Rate A charges a fixed fee of $10 plus $2 per pound of package weight. Rate B charges a fixed fee of $15 plus $1.50 per pound of package weight. How much should a package weigh for both rates to charge the same amount?
Let be the weight of the package we want to ship. We look for a weight such that:
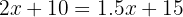
Then, we solve for the weight:
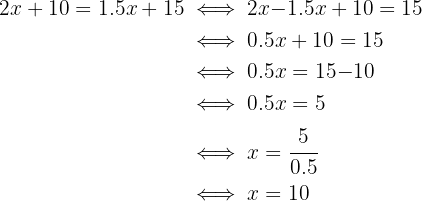
Then, for both rates to be equal, our package must weigh 10 pounds.
A customer is comparing two cell phone plans. Plan A offers a fixed monthly cost of $30 plus $0.10 per minute of calls. Plan B offers a fixed monthly cost of $45 plus $0.05 per minute of calls. How many minutes must the customer use for both plans to charge the same amount?
Let be the number of minutes the customer uses. Then, we look for a number of minutes such that:
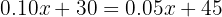
That is, an such that the rate of both plans is equal.
Then, we solve for the time in minutes:
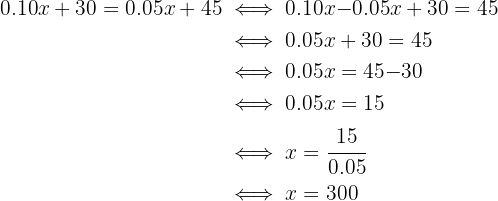
Then, at 300 minutes of service, both rates coincide.
Did you like this article? Rate it!
Loading...
