The exercises that we will solve below are examples of:
- Factoring a binomial
- Factoring a perfect square trinomial
- Factoring a perfect square trinomial
- Factoring a second-degree trinomial
- Factoring a fourth-degree polynomial
- Factoring an incomplete third-degree polynomial
- Ordering the equation to facilitate factorization
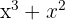
1 To factor 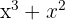 , we notice that
, we notice that  is a common factor of both terms
is a common factor of both terms
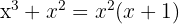
2 We know that the roots are the value that  takes such that the equation equals zero, so, given
takes such that the equation equals zero, so, given 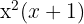 , there are 2 cases: when
, there are 2 cases: when  and when
and when 
Thus, the roots are  and
and 
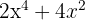
1 To factor 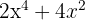 , we notice that
, we notice that 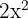 is a common factor of each of the terms
is a common factor of each of the terms
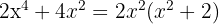
2 In this case only the root  exists, since the polynomial
exists, since the polynomial  has no roots, that is, there is no real number
has no roots, that is, there is no real number  such that
such that 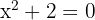

1 We apply difference of squares
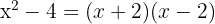
2 Setting each factor equal to zero gives us the roots
 y
y 
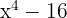
1 We apply difference of squares

2 We apply difference of squares again to the second factor

3 Setting each factor equal to zero gives us the roots
 y
y 
Remember that the factor  has no real roots.
has no real roots.
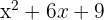
1 We have a perfect square trinomial, which can be written as a binomial squared, for which we have to ask ourselves:
What number squared gives  , what number squared gives
, what number squared gives  and verify that twice the product of the two results equals
and verify that twice the product of the two results equals 
2 The above is satisfied for  and
and  , so the factorization is expressed as follows
, so the factorization is expressed as follows

3 Setting each factor equal to zero gives us the roots
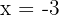 and it is said to be a double root.
and it is said to be a double root.

1 In this case we will use the quadratic formula for which we must set the equation equal to zero, that is  . We find the values of
. We find the values of  (roots of the equation) using the quadratic formula
(roots of the equation) using the quadratic formula
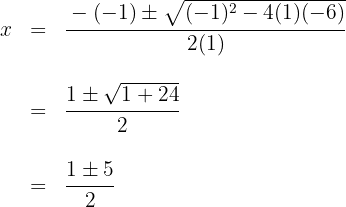
Solving, we obtain the roots 
2 In this case the factors of the given equation are
 .
.

1 We set the polynomial equal to zero and make a variable substitution 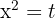
Substituting our new variable we have 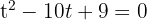
2 We solve the quadratic equation
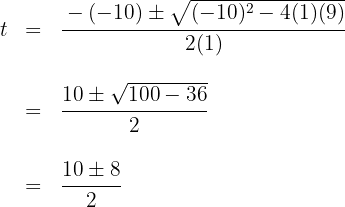
Solving, we obtain the roots 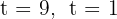
3 Now, in our variable substitution we had 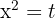 ; we undo the variable substitution and obtain the roots
; we undo the variable substitution and obtain the roots

4 In this case the factors of the given equation are
 .
.
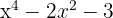
1 We set the polynomial equal to zero and make a variable substitution 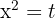
Substituting our new variable we have 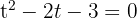
2 We solve the quadratic equation

Solving, we obtain the roots 
3 Now, in our variable substitution we had 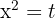 ; we undo the variable substitution and obtain the roots
; we undo the variable substitution and obtain the roots
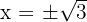 ; but
; but 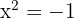 has no real solutions
has no real solutions
4 In this case the factors of the given equation are
 .
.
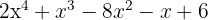
1 We take the divisors of the constant term, these are  .
.
2 Applying the remainder theorem we will know for which values the division is exact.

3 We divide by synthetic division.
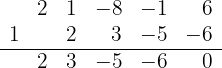
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as

4 We continue performing the same operations on the second factor. We test  again because the first factor could be squared.
again because the first factor could be squared.

Then  is not a root of the second factor. We test with
is not a root of the second factor. We test with 
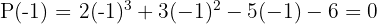
5 We divide by synthetic division.
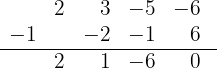
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as
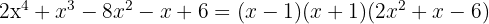
6 We can find the third factor by applying the quadratic equation or as we have been doing, although it has the disadvantage that we can only find integer roots.
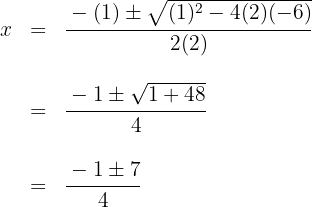
The roots are 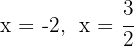 and the polynomial is expressed as
and the polynomial is expressed as
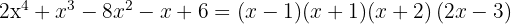

1 We take the divisors of the constant term, these are 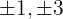 .
.
2 Applying the remainder theorem we will know for which values the division is exact.
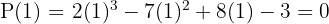
3 We divide by synthetic division.
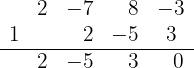
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as

4 We continue performing the same operations on the second factor. We test  again because the first factor could be squared.
again because the first factor could be squared.

5 We divide by synthetic division.

Since the division is exact,  is a double root and the polynomial is expressed as
is a double root and the polynomial is expressed as
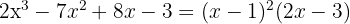
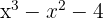
¹ We take the divisors of the constant term, these are 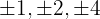 .
.
² Applying the remainder theorem we will know for which values the division is exact.
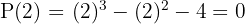
³ We divide by synthetic division.
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as
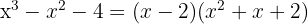
⁴ We can find the second factor by applying the quadratic equation or as we have been doing, although it has the disadvantage that we can only find integer roots.
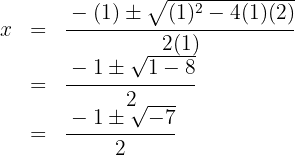
Since the discriminant is negative, the polynomial has no real roots. Thus, the only root is  and the polynomial is expressed as
and the polynomial is expressed as
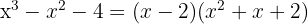
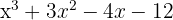
¹ We take the divisors of the constant term, these are 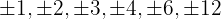 .
.
² Applying the remainder theorem we will know for which values the division is exact.

³ We divide by synthetic division.
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as
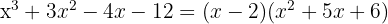
⁴ We can find the second factor by applying the quadratic equation or as we have been doing, although it has the disadvantage that we can only find integer roots.
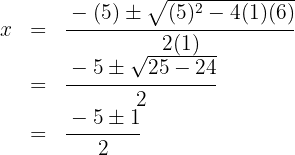
The roots of the second factor are 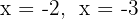 and the polynomial is expressed as
and the polynomial is expressed as
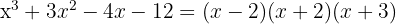
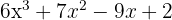
¹ We take the divisors of the constant term, these are  .
.
² Applying the remainder theorem we will know for which values the division is exact.
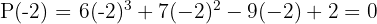
³ We divide by synthetic division.
Since the division is exact,  is a root and the polynomial is expressed as
is a root and the polynomial is expressed as

⁴ We can find the second factor by applying the quadratic equation or as we have been doing, although it has the disadvantage that we can only find integer roots.
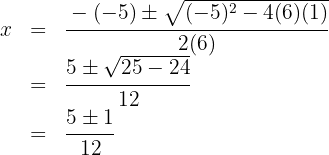
The roots of the second factor are  and the polynomial is expressed as
and the polynomial is expressed as

Factor the following polynomials:
a 
b 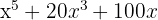
c 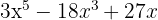
d 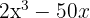
e 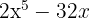
f 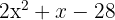
a 
We factor out the common factor 
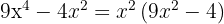
We write the difference of squares as a sum times a difference
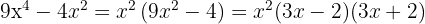
b 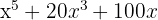
We extract the common factor 

We have a perfect square trinomial that we can express as a binomial squared
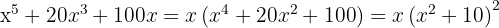
c 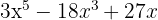
We extract the common factor 
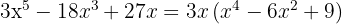
We have a perfect square trinomial that we can express as a binomial squared
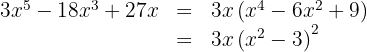
We write the difference of squares as a sum times a difference
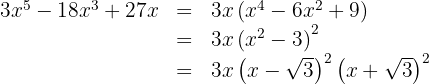
d 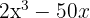
We factor out the common factor 
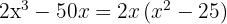
We write the difference of squares as a sum times a difference

e 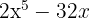
We extract the common factor 

We write the difference of squares as a sum times a difference
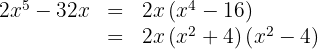
The second factor is an irreducible or prime polynomial
The third factor is a difference of squares that we factor as a sum times a difference
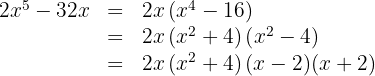
f 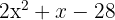
We set the quadratic trinomial equal to zero and solve the equation

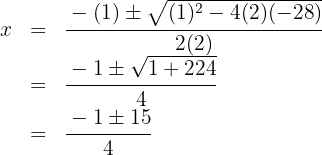
The roots are 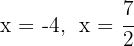 and the polynomial is expressed as
and the polynomial is expressed as
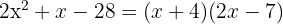
Factor the following polynomials:
a 
b 
c 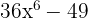
d 
e 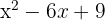
f 
g 
h 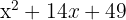
i 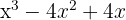
j 
k 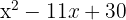
l 
m 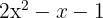
a 
In this exercise we can do a double extraction of common factors. In the first two terms we extract  and in the last two we extract
and in the last two we extract 

We factor out the common factor 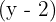

b 
is a difference of squares
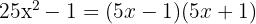
c 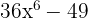
The difference of squares equals a sum times a difference
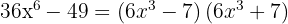
d 
A perfect square trinomial equals a binomial squared
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 

e 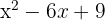
A perfect square trinomial equals a binomial squared
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 
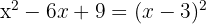
f 
A perfect square trinomial equals a binomial squared
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 
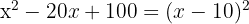
g 
A perfect square trinomial equals a binomial squared
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 

h 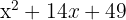
A perfect square trinomial equals a binomial squared
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 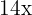
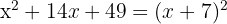
i 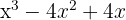
We factor out the common factor

We have another perfect square trinomial
The square of  is
is  , the square of
, the square of  is
is  and twice the first
and twice the first  times the second
times the second  is
is 
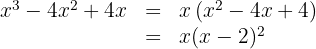
j 
We factor out the common factor
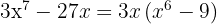
We transform the difference of squares into a sum times a difference

We apply sum and difference of cubes
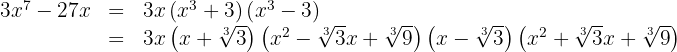
k 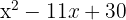
We set the polynomial equal to zero
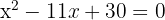
We solve the quadratic equation
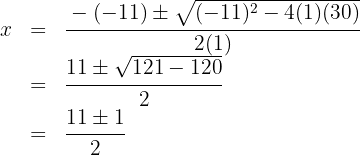
The roots are 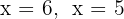 and the polynomial is expressed as
and the polynomial is expressed as

l 
We solve the quadratic equation
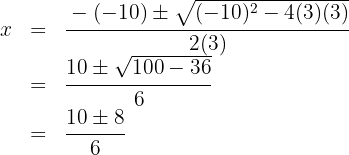
The roots are 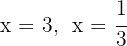 and the polynomial is expressed as
and the polynomial is expressed as
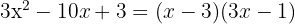
m 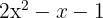
We solve the quadratic equation
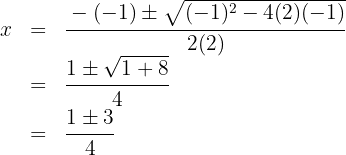
The roots are 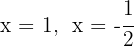 and the polynomial is expressed as
and the polynomial is expressed as

If you prefer to learn from home, why not look for an online math teacher? The first class with Superprof is free!


