Welcome to our page dedicated to exercises and problems with first-degree equations! Here, we will explore how linear equations can be the key to solving a variety of everyday problems. From calculating dimensions of places to calculating ratios, distances and ages, first-degree equations are everywhere.

In this space, you will learn how to translate real-life situations into simple equations and then solve them effectively. Our goal is to show you how mathematics is much more than numbers on a page; they are powerful tools that can help you make informed decisions and solve problems in your daily life. Join us on this journey as we discover how first-degree equations can make life simpler and more exciting at the same time!

1

A father is 35 years old and his son is 5. After how many years will the father's age be three times greater than the son's age?

Solution

1 Son's age in years:

2 Father's age in years:

3 The father's age equals three times the son's age in years

4 We remove parentheses

5 We group terms and solve by dividing by 2

6 The answer is: after 10 years.

2

If double a number is subtracted by its half, the result is 54. What is the number?

Solution

1 Number:

2 Double the number:

3 Half the number:

4 If we subtract the half from double the number we get 54

5 We eliminate denominators, group terms and solve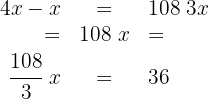

6 The number we're looking for is: 36

3

The base of a rectangle is double its height. What are its dimensions if the perimeter measures 30 cm?

Solution

1 Height:

2 Base:

3 The perimeter of a rectangle is the sum of double the height plus double the base

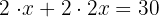
4 We add and solve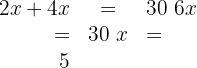

5 The height we're looking for is: 5 cm
The base we're looking for is: 10 cm

4

At a gathering there are double the number of women than men and triple the number of children than men and women together. How many men, women and children are there if the gathering consists of 96 people?

Solution

1 Men

2 Women

3 Children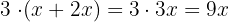

4 In total there are 96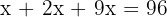

5 We add and solve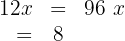

6 Men: 8 Women:
16 Children: 72

5

7/8 of an oil drum has been consumed. We replenish 38 oz and the drum is filled to 3/5 of its capacity. Calculate the capacity of the drum.

Solution

1 We call the capacity of the drum and since we have consumed 7/8 of its capacity there will remain: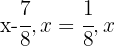

2 If we replenish 38 oz, 3/5 of the drum's capacity is filled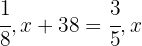

3 We eliminate denominators, the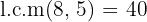

4 We group terms and solve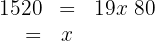

5 The capacity of the drum is: 80 oz

6

A farm has pigs and turkeys, in total there are 35 heads and 116 legs. How many pigs and turkeys are there?

Solution

1 Pigs

2 Turkeys

3 The total number of legs will be four times the number of pigs plus twice the number of turkeys.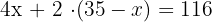

4 We remove parentheses

5 We group and solve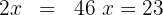

6 Pigs: 23
Turkeys: 35 - 23 = 12

7

Louis made a car trip in which he consumed 20 gallons of gasoline. He made the journey in two stages: in the first, he consumed 2/3 of the gasoline that was in the tank and in the second stage, half of the remaining gasoline. How many gallons of gasoline did the tank have and how much did he consume in each stage?

Solution

1 Gallons of gasoline in the tank:
First stage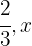
Second stage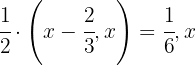

2 Between the two stages he has consumed 20 gallons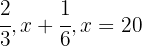

3 We eliminate denominators, add and solve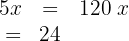

4 The results we're looking for are:
Amount in the tank: 24 gallons
Amount consumed in the first stage: 16 gallons
Amount consumed in the second stage: 4 gallons

8

In a bookstore, Ana buys a book with one-third of her money and a comic with two-thirds of what she had left. When leaving the bookstore she had $12. How much money did Ana have?

Solution

1 Total
Book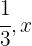
Comic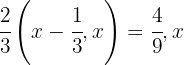

2 The money the book costs, plus the comic, plus the money she had left will equal the money she had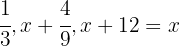

3 We eliminate denominators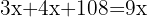

4 We group terms and solve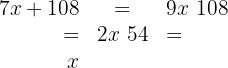

5 Ana had $54 

9

The two digits of a number are consecutive. The larger is in the tens place and the smaller in the units place. The number equals six times the sum of the digits. What is the number?

Solution

1 Units
Tens

2 If we have a two-digit number, for example 65, we can decompose it like this: 6 · 10 + 5.

3 Our two-digit number is: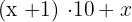

4 Since this number is six times greater than the sum of its digits: , we will have: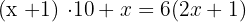

5 We remove parentheses and solve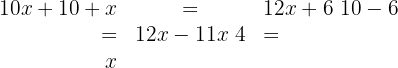

6 The results are:
Units: 4
Tens: 5
Number: 54

10

Three-fourths of John's father's age exceeds John's age by 15 years. Four years ago the father's age was double the son's age. Find both ages.

Solution

1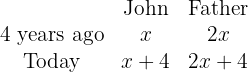

2 We set up the problem

3 We remove parentheses, group terms and solve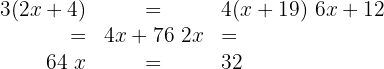

4 The ages are:
John: 32 + 4 = 36
Father: 2 · 32 + 4 = 68

11

Working together, two workers take 14 hours to do a job. How long will it take them to do it separately if one is twice as fast as the other?

Solution

1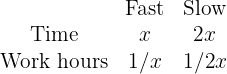

2 We set up the problem

2 We calculate the l.c.m. to eliminate denominators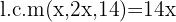

3 We multiply both sides and solve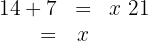

4 The results are:
Fast: 21 hours
Slow: 42 hours

12

Find the value of the three angles of a triangle knowing that B measures 40° more than C and that A measures 40° more than B.

Solution

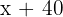1 C: B: A: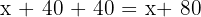

2 The sum of the angles of a triangle equals 180º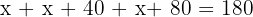

3 We group terms

4 We add and solve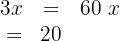

5 The angles are: C = 20º, B = 20º + 40º = 60º, A = 60º + 40º = 100º

13

A plot of land has dimensions of 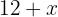feet long and 11 feet wide. If its area is 220 square feet, determine the value of .

Solution

1 Length of the plot: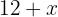

2 Width of the plot:

3 The area of the plot is 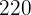square feet: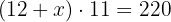

4 We remove parentheses

5 We solve for

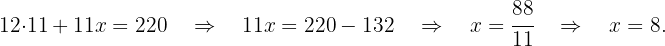
6 The answer is: .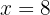

14

If ten times a number is subtracted by two-thirds of the same number, the result is 56, what is that number?

Solution

1 Number:

2 Ten times the number:

3 Two-thirds of the number: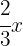

4 Ten times a number subtracted by two-thirds of the same results in 56:

5 We solve for :

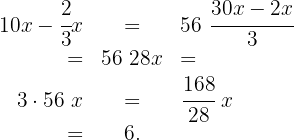
6 The answer is: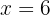

15

Two-fifths of a garden hose equals 60 feet. How long is the complete hose?

Solution

1 Length of the hose:

2 Two-fifths of the hose equals 60 feet: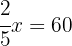

3 We solve the equation for :

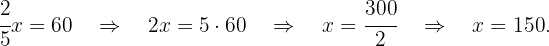
4 The length of the hose is feet.

At Superprof we have the best mathematics courses to help you with all your doubts.

Did you like this article? Rate it!

5.00 (1 Note(n))
Loading...

Agostina

Agostina Babbo is an English and Italian to Spanish translator and writer, specializing in product localization, legal content for tech, and team sports—particularly handball and e-sports. With a degree in Public Translation from the University of Buenos Aires and a Master's in Translation and New Technologies from ISTRAD/Universidad de Madrid, she brings both linguistic expertise and technical insight to her work.