First-Degree Equations 101

First-degree equations are some of the most fundamental building blocks in algebra! If you've ever wondered "what value of x makes this equation true?", you've already started thinking about solving equations.

These equations might seem simple, but they're incredibly powerful. Once you master first-degree equations, you'll have the foundation you need to tackle more complex problems like quadratic equations, cubic equations, and even advanced topics in calculus. Think of them as your mathematical stepping stones to bigger concepts.

So, what exactly is a first-degree equation? It's an equation where the variable (usually x) appears only to the first power - no squares, cubes, or higher powers. The highest exponent you'll see is 1, which is why we call it "first-degree."

In general, there's a reliable step-by-step process to solve any first-degree equation:

1 Remove parentheses - Distribute and simplify

2 Clear denominators - Get rid of fractions by multiplying

3 Group like terms - Put all the terms on one side, numbers on the other

4 Combine like terms - Simplify each side

5 Solve for the unknown - Isolate x to find your answer

Let's see this in action!

Example:

Solve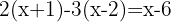

1 We remove parentheses.

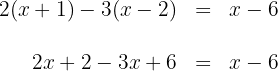
2 We group the terms with on one side and the independent terms on the other.

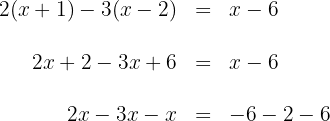
3 We combine like terms.

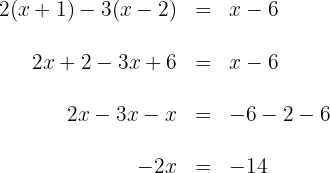
4 We solve for the unknown.

Example:

Solve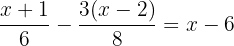

1 We remove parentheses.

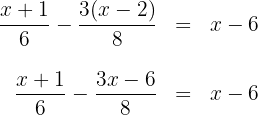
2 We remove denominators by multiplying both sides by the least common multiple of the denominators .

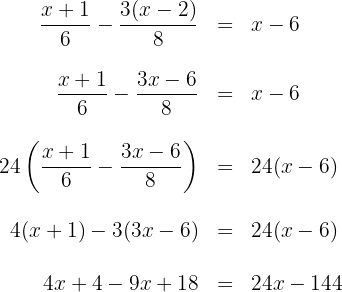
3 We group the terms with on one side and the independent terms on the other.

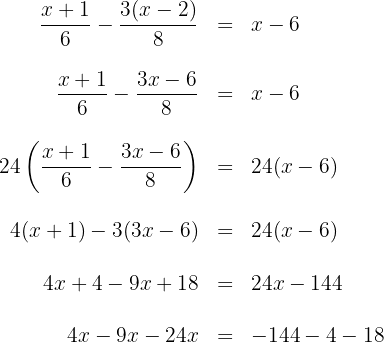
4 We combine like terms.

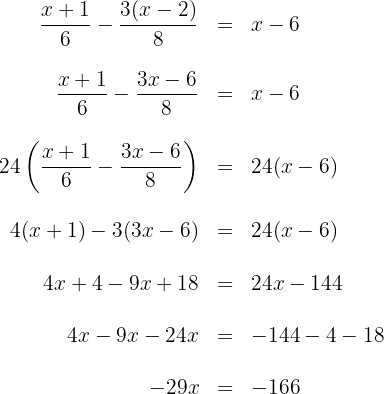
5 We solve for the unknown.

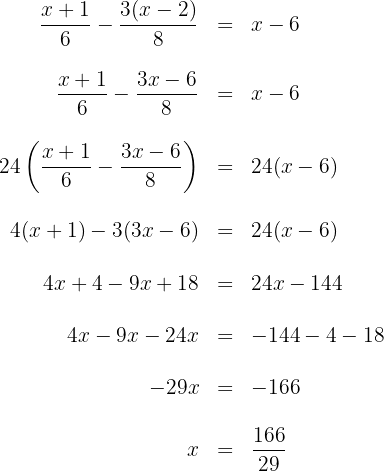
With practice, these steps will become second nature. Keep working with us!