Welcome to the fascinating world of fractions! If you have ever found mathematical problems involving these small parts of a whole challenging, you have come to the right place. On this page dedicated to fraction problems, we will explore countless situations where these numerical pieces become the key to solving puzzles and real-world situations.
Our team of mathematics enthusiasts will guide you through practical and challenging problems, demystifying the world of fractions and showing you how to apply these skills in your daily life.
So, if you're ready to dive into the exciting universe of fractions and unlock their power to solve problems, this page is for you. Get ready to explore the magic behind fractional numbers and take your mathematical skills to the next level!
Let's start solving fraction problems together!

Fractions and The Units They Represent
Calculate what fraction of the unit these represent:
a Half of a half.
b Half of a third.
c A third of a half.
d Half of a fourth.
e A fourth of a half.
a Half of a half.
Half of a number  is written as
is written as
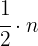
Since the number  is a half, then we obtain
is a half, then we obtain
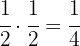
b Half of a third.
Half of a number  is written as
is written as
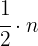
Since the number  is a third, then we obtain
is a third, then we obtain

c A third of a half.
A third of a number  is written as
is written as
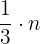
Since the number  is a half, then we obtain
is a half, then we obtain

d Half of a fourth.
Half of a number  is written as
is written as

Since the number  is a fourth, then we obtain
is a fourth, then we obtain

e A fourth of a half.
A fourth of a number  is written as
is written as
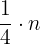
Since the number  is a half, then we obtain
is a half, then we obtain

Daily Life Problems Using Fractions
To prepare a cake, you need: 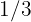 of a package of
of a package of  of sugar,
of sugar, 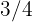 of a package of flour weighing
of a package of flour weighing  and
and 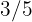 of a stick of butter weighing
of a stick of butter weighing  . Find, in pounds, the quantities needed to prepare the cake.
. Find, in pounds, the quantities needed to prepare the cake.
We write in pounds each of the quantities needed to prepare the cake.
 of a package of
of a package of  of sugar
of sugar

 of a package of flour weighing
of a package of flour weighing 

 of a stick of butter weighing
of a stick of butter weighing 

From a piece of fabric measuring  ,
, 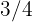 is cut. How many feet does the remaining piece measure?
is cut. How many feet does the remaining piece measure?
We calculate how many feet  equals
equals
 .
.
We subtract it from the  .
.
 .
.
A box contains  chocolates. Eva ate
chocolates. Eva ate 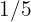 of the chocolates and Ana
of the chocolates and Ana  .
.
a How many chocolates did Eva eat and how many did Ana eat?
b What fraction of chocolates did they eat together?
a How many chocolates did Eva eat and how many did Ana eat?
We multiply  by the corresponding fraction for Eva and Ana.
by the corresponding fraction for Eva and Ana.

Eva ate  and Ana
and Ana  .
.
b What fraction of chocolates did they eat together?
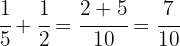
A few years ago Peter was  years old, which represents
years old, which represents  of his current age. How old is Peter?
of his current age. How old is Peter?
We represent it graphically.
 equals two of the three parts of his age, so we calculate how much one part is worth (24÷2) and multiply the result by the total number of parts, which is
equals two of the three parts of his age, so we calculate how much one part is worth (24÷2) and multiply the result by the total number of parts, which is  .
.

Therefore, Peter is  years old.
years old.
 of a neighborhood community's income is used for fuel,
of a neighborhood community's income is used for fuel, 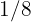 is used for electricity,
is used for electricity, 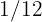 for garbage collection,
for garbage collection, 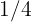 for building maintenance and the rest is used for cleaning.
for building maintenance and the rest is used for cleaning.
a What fraction of income is used for cleaning?
b According to the fraction of income used, order the listed items from least to greatest.
a What fraction of income is used for cleaning?
To solve this, we must add the fractions of each of the other items and subtract this result from  . Thus
. Thus

Subtracting our previous result from  we obtain
we obtain
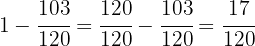
Therefore, 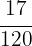 of the income was used for cleaning.
of the income was used for cleaning.
b According to the fraction of income used, order the listed items from least to greatest

Taking the fractions with the same denominator

In local elections held in a town, 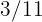 of the votes went to party
of the votes went to party  ,
, 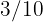 to party
to party  ,
, 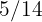 to
to  and the rest to party
and the rest to party  . The total number of votes was
. The total number of votes was  . Calculate:
. Calculate:
a The number of votes obtained by each party.
b The number of abstentions knowing that the number of voters represents 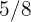 of the electoral census.
of the electoral census.
a The number of votes obtained by each party.
Party A: 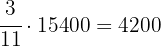
Party B: 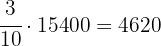
Party C: 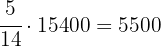
Party D: 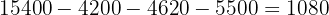
b The number of abstentions knowing that the number of voters represents  of the electoral census.
of the electoral census.
Note that the total voters is  , that is, it is
, that is, it is  , therefore, the fraction of abstentions is
, therefore, the fraction of abstentions is
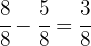
Thus, the number of abstentions using the rule of three is given by
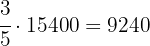
The line is divided into  equal parts. To know the amount that each part represents, we take into account that the first
equal parts. To know the amount that each part represents, we take into account that the first  parts (the votes) add up to
parts (the votes) add up to  , therefore one part will be
, therefore one part will be 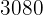 multiplied by
multiplied by  which equals
which equals  . And the other three parts (the abstentions) are obtained by multiplying
. And the other three parts (the abstentions) are obtained by multiplying  by
by 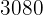 .
.
George earns $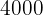 per month and allocates the following fractions of his salary to the following categories:
per month and allocates the following fractions of his salary to the following categories: 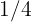 for rent,
for rent, 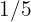 for food,
for food, 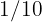 for gas,
for gas, 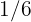 for household services and clothing, and
for household services and clothing, and 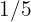 for personal expenses. If George saves the remainder:
for personal expenses. If George saves the remainder:
a What fraction does George save?
b How much does this fraction correspond to in money?
a What fraction does George save?
To solve this, we must add each fraction and subtract the result from  . Thus
. Thus

Subtracting our previous result from  we obtain
we obtain
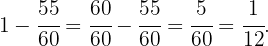
Therefore, George saves 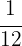 of his monthly income.
of his monthly income.
b How much does this fraction correspond to in money?
To know how much this fraction corresponds to in money, we multiply it by the total income

Thus, George saves approximately $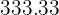 per month.
per month.
The history subject will be graded according to the following criteria: 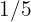 exam,
exam, 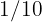 participation,
participation, 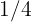 assignments,
assignments, 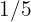 project,
project, 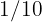 punctuality and the rest in attendance. What fraction does attendance represent of the total grade?
punctuality and the rest in attendance. What fraction does attendance represent of the total grade?
To solve this, we must add each fraction and subtract the result from  . Thus
. Thus

Subtracting our previous result from  we obtain
we obtain
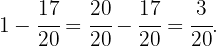
Therefore, 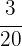 corresponds to attendance.
corresponds to attendance.
A farmer plants his  acre plot every year with the following proportions:
acre plot every year with the following proportions: 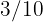 wheat,
wheat, 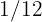 beans,
beans, 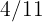 barley, and the rest with corn. What fraction of the land should be planted with corn?
barley, and the rest with corn. What fraction of the land should be planted with corn?
To solve this, we must add the fractions and subtract the result from  . Thus
. Thus

Subtracting our previous result from  we obtain
we obtain
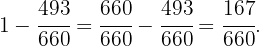
Therefore, 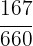 of the land will be planted with corn.
of the land will be planted with corn.
Phoebe plans to read a 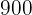 page book she bought last week. Since she has different activities during the week, she plans to read an average of
page book she bought last week. Since she has different activities during the week, she plans to read an average of  pages every day from Monday to Friday, and on Saturday and Sunday,
pages every day from Monday to Friday, and on Saturday and Sunday,  pages each day.
pages each day.
a What fraction of the total represents the pages that Fabiola can read each day of the week?
b How long will it take her to read the book?
a What fraction of the total represents the pages that Phoebe can read each day of the week?
Let  be the fraction of pages that Phoebe can read Monday through Friday. Thus, we have the following relationship:
be the fraction of pages that Phoebe can read Monday through Friday. Thus, we have the following relationship:

We solve for 

Therefore, each day from Monday to Friday, Phoebe reads 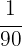 of the total pages in the book.
of the total pages in the book.
Similarly for Saturday and Sunday, we have the relationship

Solving

Thus, both Saturday and Sunday, Phoebe reads 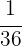 of the total pages in the book.
of the total pages in the book.
b How long will it take her to read the book?
Since each day from Monday to Friday, Phoebe reads  pages, then in these
pages, then in these  days she will read
days she will read  pages. Similarly, on Saturday and Sunday, Phoebe reads
pages. Similarly, on Saturday and Sunday, Phoebe reads  pages. Thus, each week she will read
pages. Thus, each week she will read  pages. Therefore, it will take her
pages. Therefore, it will take her  weeks to read the book.
weeks to read the book.
Fractions and Gallons
A tank contains  gallons of water.
gallons of water.  of its contents are consumed. How many gallons of water remain?
of its contents are consumed. How many gallons of water remain?
The total water content is 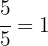 and we consume
and we consume  , therefore what remains is:
, therefore what remains is:

A family has consumed on a summer day: Two bottles of a gallon and a half of water, four cans of 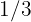 gallon of juice and five lemonades of
gallon of juice and five lemonades of 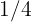 gallon. How many gallons of liquid have they drunk? Express the result as a mixed number.
gallon. How many gallons of liquid have they drunk? Express the result as a mixed number.
First we convert the gallon and a half to a fraction.

We multiply each number of items by its corresponding fraction. We find a common denominator and add
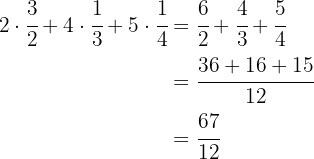
We divide the numerator by the denominator  , the quotient
, the quotient  is the whole number of the mixed number, the remainder
is the whole number of the mixed number, the remainder  is the numerator of the fraction and the denominator is the same as the improper fraction
is the numerator of the fraction and the denominator is the same as the improper fraction  :
:

How many thirds of a gallon are there in  gallons?
gallons?
We divide the total gallons by one third

We can also solve it using graphics.

In  gallon there are three thirds, so in
gallon there are three thirds, so in  gallons there will be:
gallons there will be:  thirds.
thirds.
A gallon of gasoline is sold for $ . If a car's tank is filled with $
. If a car's tank is filled with $ . How many gallons does this amount represent?
. How many gallons does this amount represent?
We will convert the $ to gallons with the equivalence of
to gallons with the equivalence of  gallon costs $
gallon costs $ . Note that
. Note that
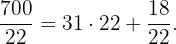
Thus,
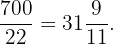
That is, for $ we would get
we would get  of gasoline.
of gasoline.
A plant in a pot is watered every  days with
days with  gallons of water. The plant consumes
gallons of water. The plant consumes 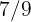 of the water it receives and the rest is drained through the pot's drainage. If the plant is watered for
of the water it receives and the rest is drained through the pot's drainage. If the plant is watered for  days. How much water was consumed and how much was drained by the plant?
days. How much water was consumed and how much was drained by the plant?
To solve this, we observe that in the period of  days, the plant was watered
days, the plant was watered  times. If each time the plant received
times. If each time the plant received  gallons of water, then in this period, the plant received
gallons of water, then in this period, the plant received  gallons of water.
gallons of water.
We multiply this amount by  to know the amount of water that was consumed by the plant. Thus,
to know the amount of water that was consumed by the plant. Thus,

Thus, the plant consumed  gallons of water.
gallons of water.
Similarly, we multiply the  gallons by
gallons by  which is the amount of water that the plant drains. Then,
which is the amount of water that the plant drains. Then,
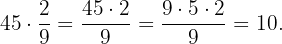
That is, the plant drained  gallons of water in this time period.
gallons of water in this time period.
Fractions and Distances
A cable  long is cut into two pieces. One piece has
long is cut into two pieces. One piece has 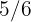 of the cable. How many feet does each piece measure?
of the cable. How many feet does each piece measure?
We calculate how many feet  equals and subtract it from
equals and subtract it from  .
.

Subtracting from 

Ana has traveled  , which is
, which is 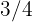 of the way from her house to the institute. What distance is there from her house to the institute?
of the way from her house to the institute. What distance is there from her house to the institute?
We represent it graphically.
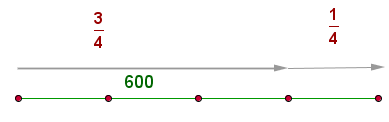
 equals three parts of the way, so we calculate how much one part is worth
equals three parts of the way, so we calculate how much one part is worth  and multiply the result by the total number of parts
and multiply the result by the total number of parts  :
:

Two automobiles  and
and  make the same
make the same  journey. Automobile
journey. Automobile  has traveled
has traveled 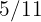 of the journey when
of the journey when  has traveled
has traveled 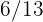 of the same. Which one is ahead? How many miles has each one traveled?
of the same. Which one is ahead? How many miles has each one traveled?
We reduce to a common denominator to compare the fractions
 is ahead.
is ahead.
Now let's analyze the distance traveled by each one:
Automobile 

Automobile 

A tailor has  yards and needs
yards and needs 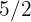 yards of fabric to make pants. How much fabric does he need to buy to make the pants?
yards of fabric to make pants. How much fabric does he need to buy to make the pants?
To solve this problem, we need to subtract from the fraction  , which is the fabric needed, the fraction
, which is the fabric needed, the fraction  , which is the fabric the tailor has. The result will be the amount needed. Thus,
, which is the fabric the tailor has. The result will be the amount needed. Thus,

Therefore, the tailor needs to buy  of fabric.
of fabric.
A tractor works  miles of land in
miles of land in  of an hour. How many miles of land will it work in
of an hour. How many miles of land will it work in 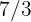 hours?
hours?
We calculate how many  of an hour there are in
of an hour there are in  hours. To do this, we calculate
hours. To do this, we calculate
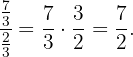
Finally, we multiply  by
by  and simplify
and simplify

Therefore, the tractor will work 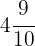 miles in this time.
miles in this time.
Fractions and Money
Elena goes shopping with $180. She spends 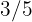 of that amount. How much does she have left?
of that amount. How much does she have left?
We calculate how much  equals and subtract it from $180.
equals and subtract it from $180.
 .
.
A father distributes $1800 among his children. He gives the oldest 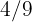 of that amount, the middle child
of that amount, the middle child 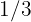 and the youngest the rest. How much did each one receive? What fraction of the money did the third one receive?
and the youngest the rest. How much did each one receive? What fraction of the money did the third one receive?
Oldest:  .
.
Middle:  .
.
Youngest: First let's calculate the fraction of money corresponding to the youngest
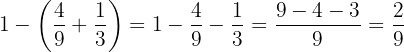 .
.
Now let's calculate the amount
 .
.
A person has a debt of $200 and paid  of it. How much is left to pay?
of it. How much is left to pay?
To solve this problem, we first calculate the amount paid and then subtract it from $200 to know the amount remaining to pay.
What was paid is  .
.
What remains to be paid is  .
.
Two friends, Louis and John, went shopping and together they spent a total of $450. If Louis spent  of what John spent, how much did each one spend?
of what John spent, how much did each one spend?
Let  be the amount spent by Louis and
be the amount spent by Louis and 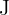 be the amount spent by John. Thus, we have the following relationships
be the amount spent by John. Thus, we have the following relationships
 .
.
We substitute the first condition into the second equation
 .
.
Therefore, John paid $300 and Louis paid
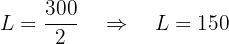
Alicia has $300 for shopping. On Thursday she spent  of that amount and on Saturday
of that amount and on Saturday 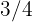 of what she had left. How much did she spend each day and how much does she have left at the end?
of what she had left. How much did she spend each day and how much does she have left at the end?
Thursday: 
Saturday: First let's calculate what she had left after Thursday

Now we need to calculate the fraction she spent from this amount

Remaining: Let's subtract from $180 the amount she spent on Saturday

We help you find the mathematics course that best suits you: do you want an online mathematics teacher? Or do you prefer to meet in-person? At Superprof you will find your ideal teacher.












