Free fall is a fundamental physical phenomenon that occurs when an object moves under the exclusive influence of gravity, without air resistance or other external forces. This concept, central to classical mechanics, allows us to understand how objects fall toward Earth and how their kinematic properties vary during this process.
Free fall exercises constitute an essential tool in the study of physics, as they allow exploring and applying the principles of kinematics in a simple but crucial context. In the following exercises we do not consider air resistance.
Exercises:
1 A ball is dropped from the top of a building, what is the velocity of the ball two seconds after it begins to fall?
Solution
1 We choose the downward direction as positive and since the ball is dropped, its initial velocity is zero
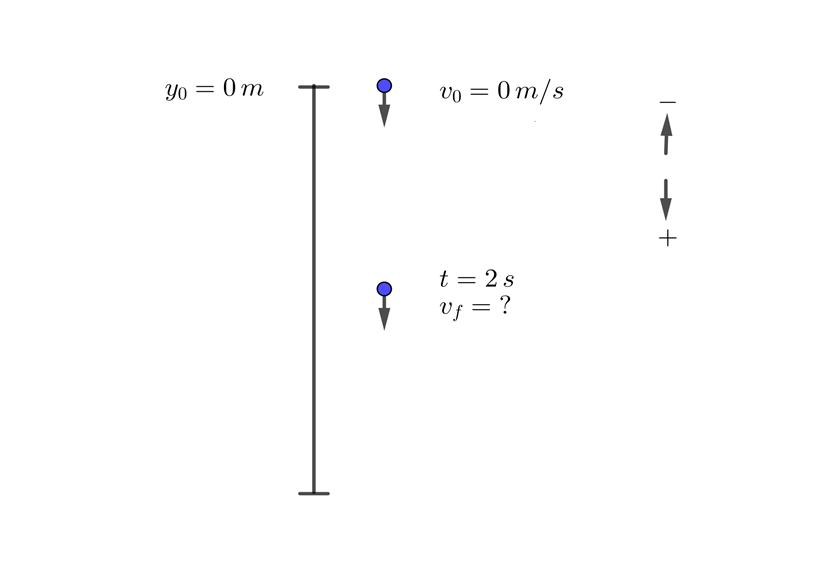
2 We indicate the known data
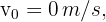
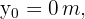
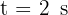
3 Since this is free fall, the acceleration equals gravity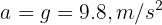 
(32.2 ft/s²), which is positive since we chose at the beginning that the downward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
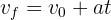
5 We substitute the known data
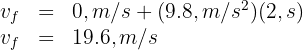
2 A ball is thrown vertically upward with velocity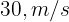 
(98.4 ft/s), what height does the ball reach? What is the time taken by the ball to fall to the ground?
Solution
1 We choose the upward direction as positive and note that its final velocity is zero
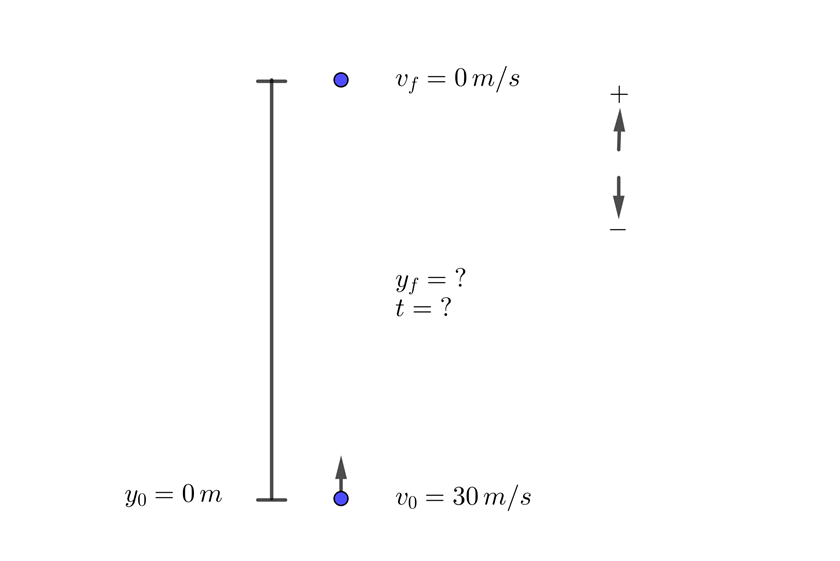
2 We indicate the known data
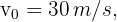
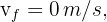
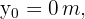
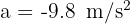
3 Since this is free fall, the acceleration equals gravity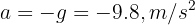 
, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
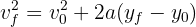
5 We substitute the known data and solve for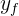 
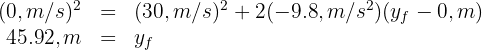
Thus, the height is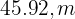 
(150.7 ft)
6 To calculate the time taken to return to the ground, we note that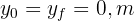 
. We use the formula
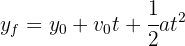
7 We substitute the known data and solve for 
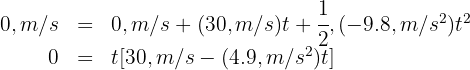
Thus, we have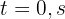 
and 
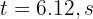. Both solutions correspond to the time when the ball is on the ground. The requested solution is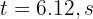
3 An object is dropped vertically from a height of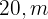 
(65.6 ft). With what velocity does the object hit the ground and how long does it take?
Solution
1 We choose the downward direction as positive and note that the initial velocity is zero
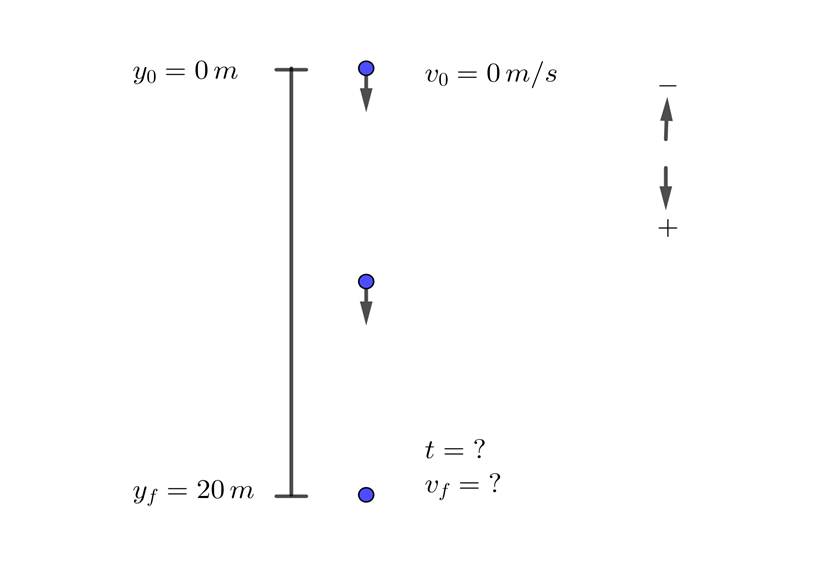
2 We indicate the known data
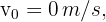
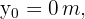
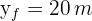
3 Since this is free fall, the acceleration equals gravity 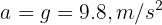, which is positive since we chose at the beginning that the downward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
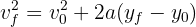
5 We substitute the known data
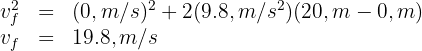
6 To find the time taken, we use the formula
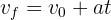
7 We substitute the known data
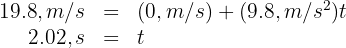
4 A ball is thrown vertically upward from the ground at a velocity of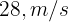 
(91.9 ft/s). How long will it take to be 30 meters (98.4 ft) above the ground?
Solution
1 We choose the upward direction as positive
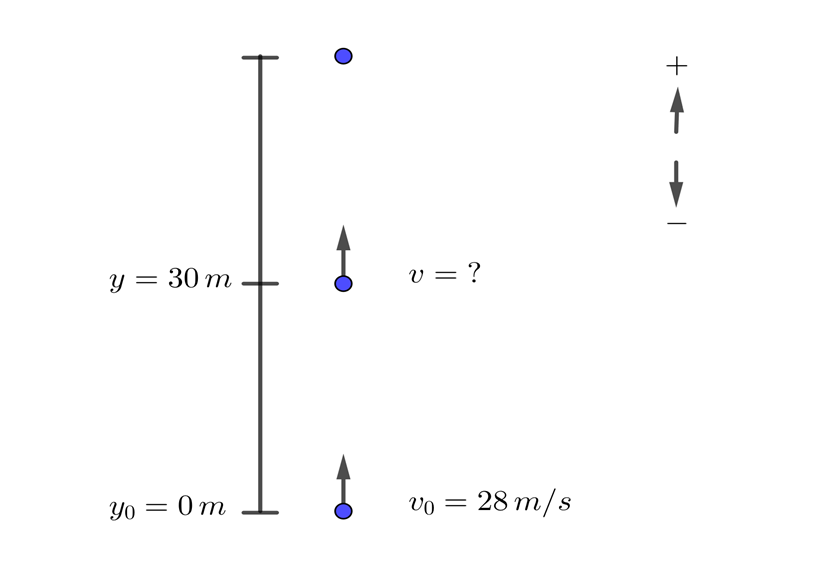
2 We indicate the known data
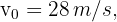
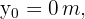
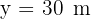
3 Since this is free fall, the acceleration equals gravity 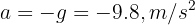, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
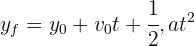
5 We substitute the known data
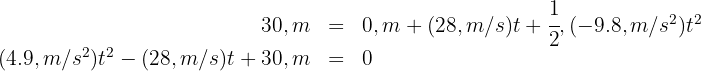
Using the quadratic formula we obtain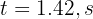 
and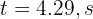 
which correspond to the time when it is going up and down respectively.
5 An object is thrown vertically upward from the ground. If it reaches a height of 18 meters (59 ft) in 3 seconds, at what velocity was the object thrown?
Solution
1 We choose the upward direction as positive
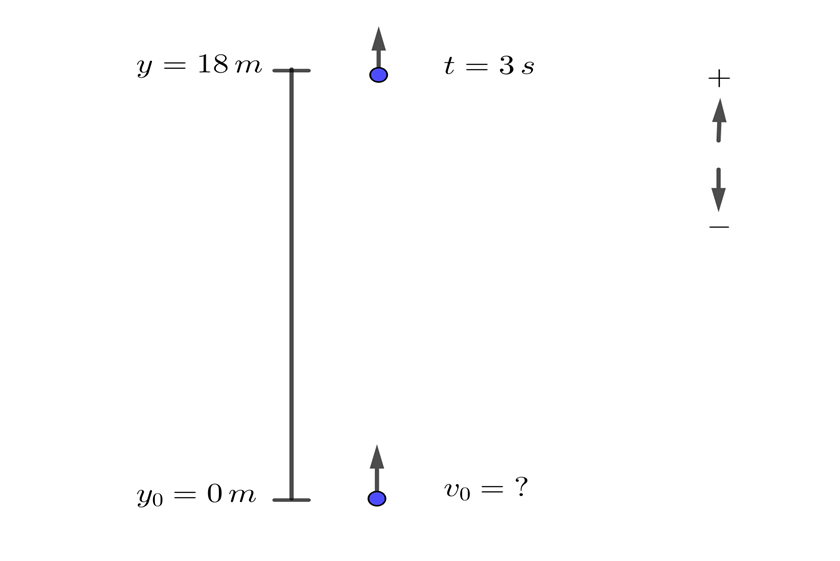
2 We indicate the known data
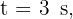
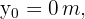
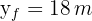
3 Since this is free fall, the acceleration equals gravity 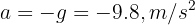, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
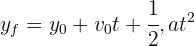
5 We substitute the known data
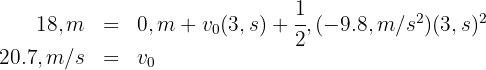
6 An object is dropped vertically downward and reaches the ground with a velocity of 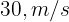(98.4 ft/s). What is the distance traveled by the object?
Solution
1 We choose the downward direction as positive and note that the initial velocity is zero
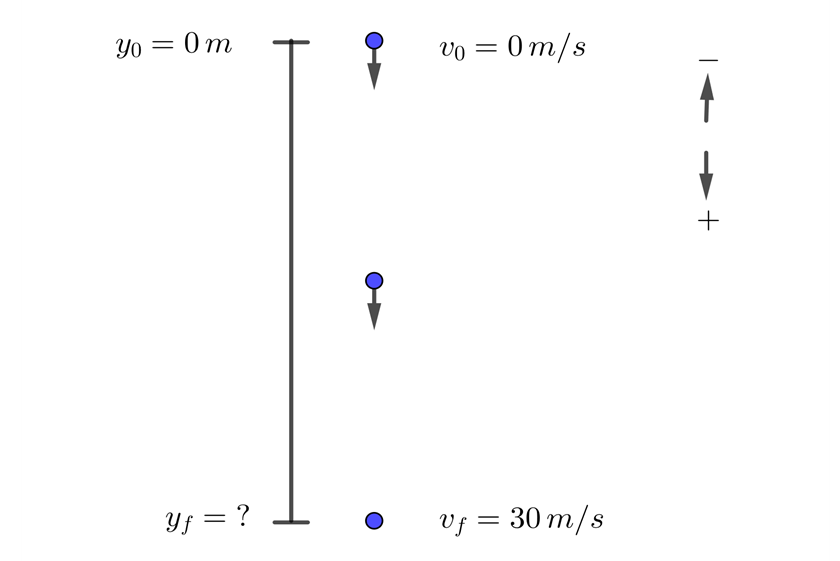
2 We indicate the known data
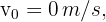
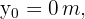
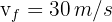
3 Since this is free fall, the acceleration equals gravity 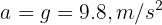, which is positive since we chose at the beginning that the downward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
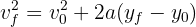
5 We substitute the known data
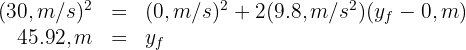
7 A ball is thrown vertically upward at a velocity of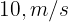 
(32.8 ft/s). In how much time does it reach the highest point of its trajectory? What is the velocity when it returns to the starting point?
Solution
1 We choose the upward direction as positive and note that at the highest point its velocity is zero.
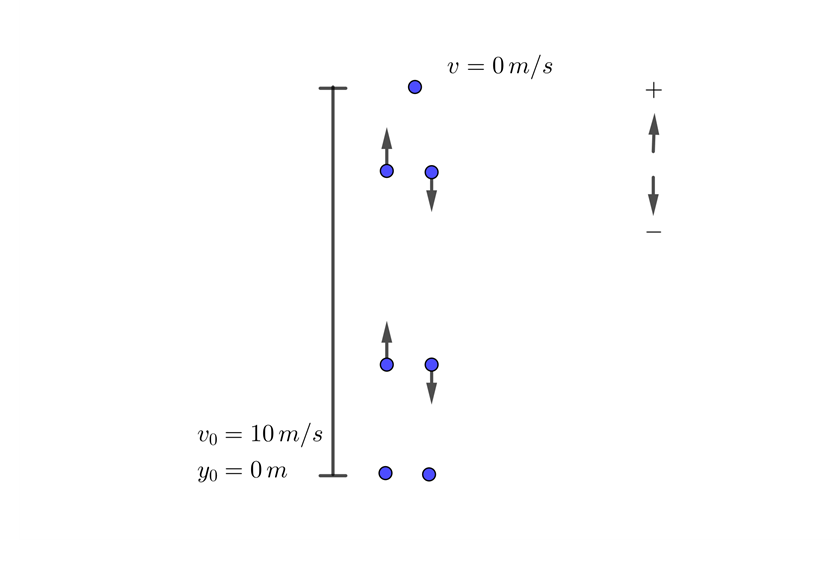
2 We indicate the known data
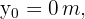
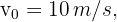
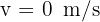
3 Since this is free fall, the acceleration equals gravity 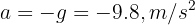, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
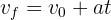
5 We substitute the known data
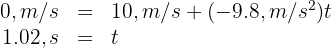
The ball reaches its highest point in 1.02 seconds
6 To calculate the velocity when it returns to the starting point, we note that the final position equals the initial position. We use the formula
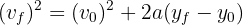
7 We substitute the known data
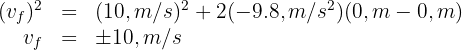
The velocity has the same magnitude as the initial one, but with opposite direction
8 A ball is thrown vertically upward at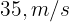 
(115 ft/s) so that it reaches its highest point and returns to its starting point. How does the ball's return velocity compare to its velocity during its ascent when passing through the same position?
Solution
1 We choose the upward direction as positive and note that at the highest point its velocity is zero.
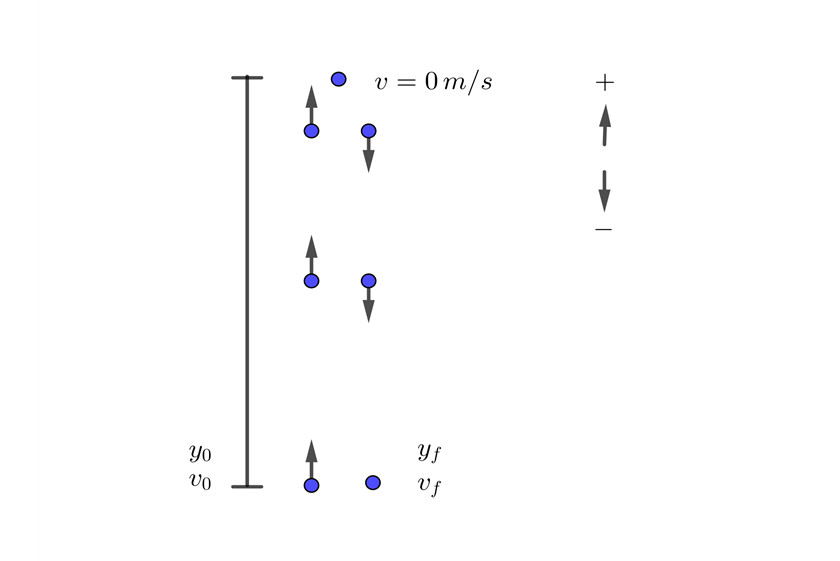
2 We indicate the known data
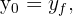
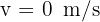
3 Since this is free fall, the acceleration equals gravity 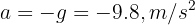, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
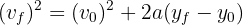
5 Since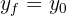 
, then
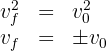
Then the magnitude of both velocities is the same, but their directions are opposite. In fact, the same occurs at each point of the ball's trajectory.
9 At what velocity must a ball be thrown vertically upward, so that after two seconds it has a velocity of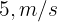 
(16.4 ft/s)?
Solution
1 We choose the upward direction as positive
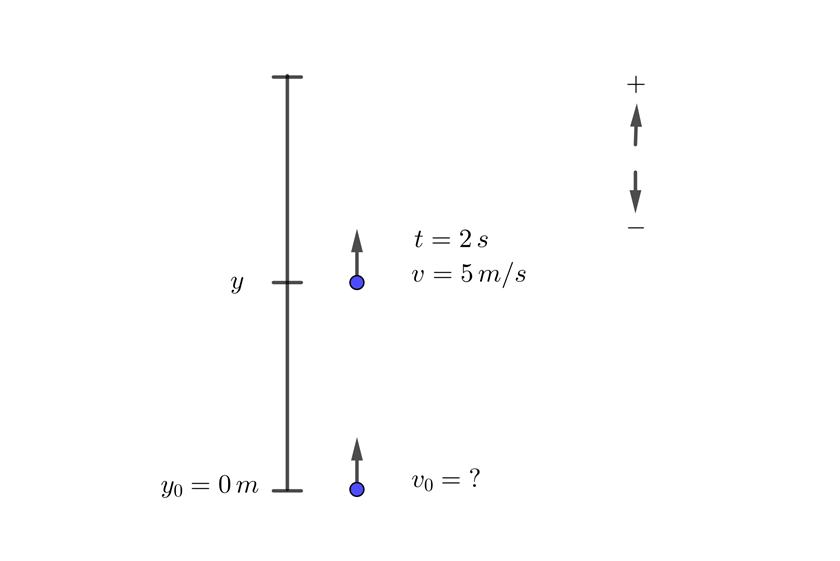
2 We indicate the known data
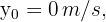
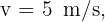
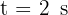
3 Since this is free fall, the acceleration equals gravity 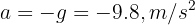, which is negative since we chose at the beginning that the upward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
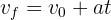
5 Substituting the known values, we obtain
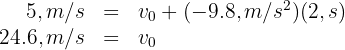
10 A ball is thrown vertically downward from the top of a building. If it travels 50 meters (164 ft) in 3 seconds, what is its initial velocity?
Solution
1 We choose the downward direction as positive
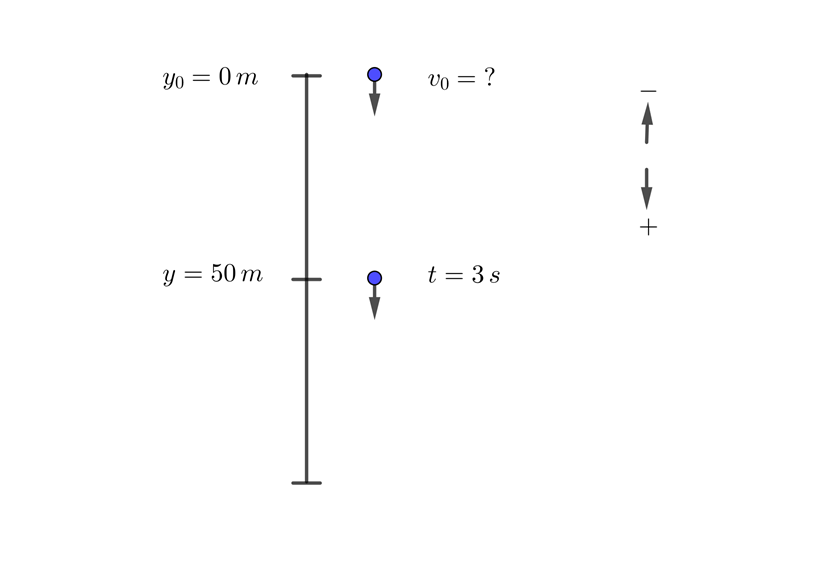
2 We indicate the known data
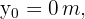
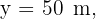
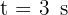
3 Since this is free fall, the acceleration equals gravity 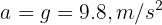, which is positive since we chose at the beginning that the downward direction is positive
4 Since the acceleration is constant, we have a uniformly accelerated motion problem, so we use the formula
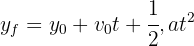
5 We substitute the known data
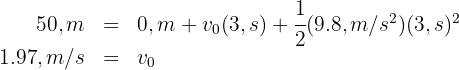
Summarize with AI:
Did you like this article? Rate it!
Loading...
