Chapters
- System of 3 Equations with 2 Variables
- System of 2 Equations with 3 Variables
- System of 3 Equations with 3 Variables with Similar Coefficients
- System of 3 Equations with 3 Variables
- Verify if the Following System Is Determined or Indeterminate
- System of 4 Equations with 4 Variables
- Verify the Indetermination of the System of 4 Equations
- Solve the System of 3 Equations and 5 Variables
- Solve the System of 4 Equations with 3 Variables
Row reduction or Gauss method is a linear algebra technique used to solve systems of linear equations and find the row echelon or reduced row echelon form of a matrix, simplifying calculations.
In this series of exercises, we will explore various problems involving Gaussian reduction, giving you the opportunity to develop your skills in this important mathematical concept. Let's start practicing!

System of 3 Equations with 2 Variables
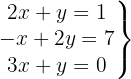
We write in matrix form

We apply the Gauss method
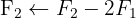
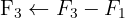

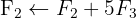

The system is consistent and determined
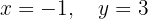
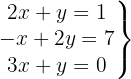
We write in matrix form
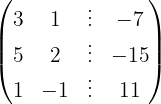
We apply the Gauss method
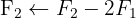
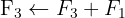

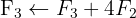

The system is consistent and determined
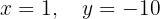
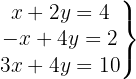
We write in matrix form

We apply the Gauss method
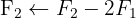
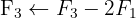

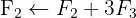
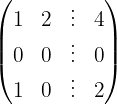
The system is consistent and determined
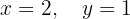
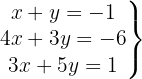
We write in matrix form
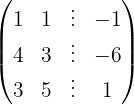
We apply the Gauss method
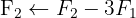
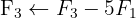

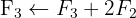

The system is consistent and determined
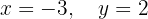
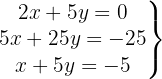
We write in matrix form
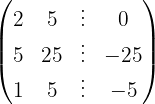
We apply the Gauss method
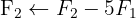
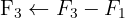
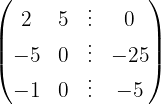
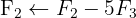

The system is consistent and determined
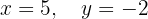
System of 2 Equations with 3 Variables
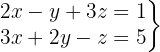
We write in matrix form
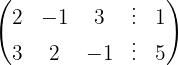
We apply the Gauss method


The system is consistent and indeterminate
We perform a parameterization of the solution using  . In this way, the second equation becomes:
. In this way, the second equation becomes:

That is, 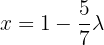 .
.
On the other hand, the first equation becomes 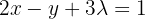 , which when solving for
, which when solving for  gives us:
gives us:
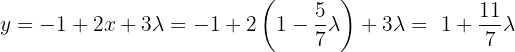
That is, 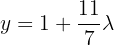 .
.
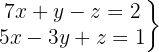
We write in matrix form
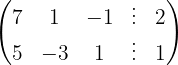
We apply the Gauss method


The system is consistent and indeterminate
We perform a parameterization of the solution using  . In this way, the second equation becomes:
. In this way, the second equation becomes:
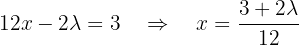
That is,  .
.
On the other hand, the first equation becomes  , which when solving for
, which when solving for  gives us:
gives us:
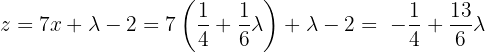
That is, 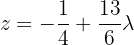 .
.
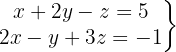
We write in matrix form
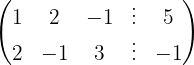
We apply the Gauss method
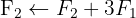
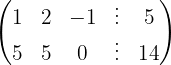
The system is consistent and indeterminate
We perform a parameterization of the solution using 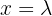 . In this way, the second equation becomes:
. In this way, the second equation becomes:
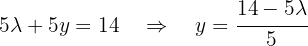
That is, 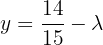 .
.
On the other hand, the first equation becomes 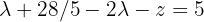 , which when solving for
, which when solving for  gives us:
gives us:
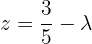
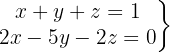
We write in matrix form
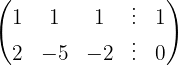
We apply the Gauss method

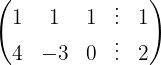
The system is consistent and indeterminate
We perform a parameterization of the solution using 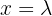 . In this way, the second equation becomes:
. In this way, the second equation becomes:
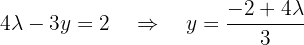
That is, 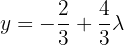 .
.
On the other hand, the first equation becomes 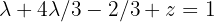 , which when solving for
, which when solving for  gives us:
gives us:
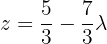
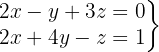
We write in matrix form
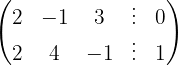
We apply the Gauss method
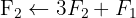
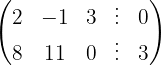
The system is consistent and indeterminate
We perform a parameterization of the solution using 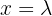 . In this way, the second equation becomes:
. In this way, the second equation becomes:
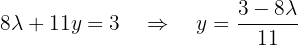
That is,  .
.
On the other hand, the first equation becomes 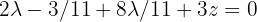 , which when solving for
, which when solving for  gives us:
gives us:
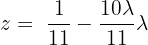
System of 3 Equations with 3 Variables with Similar Coefficients
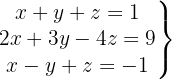
We write in matrix form

We apply the Gauss method
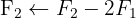
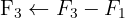
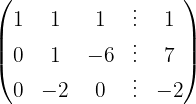
The system is consistent and determined
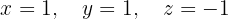
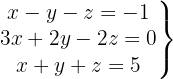
We write in matrix form

We apply the Gauss method
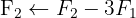
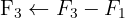
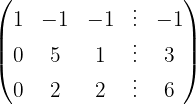

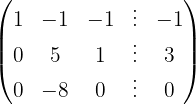
The system is consistent and determined
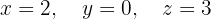
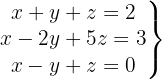
We write in matrix form
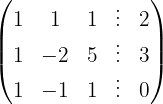
We apply the Gauss method
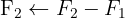
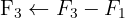

The system is consistent and determined
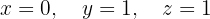
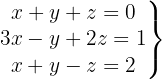
We write in matrix form
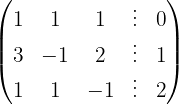
We apply the Gauss method
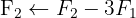
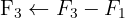
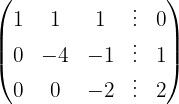
The system is consistent and determined
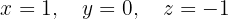
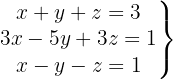
We write in matrix form
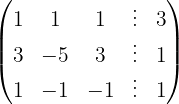
We apply the Gauss method
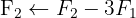
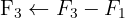
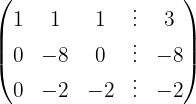
The system is consistent and determined
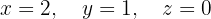
System of 3 Equations with 3 Variables
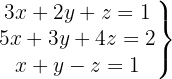
We write in matrix form
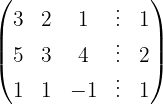
We apply the Gauss method
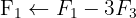
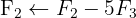

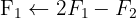
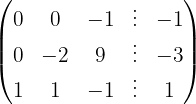
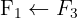
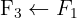
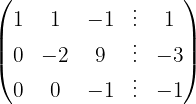
The system is consistent and determined

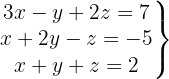
We write in matrix form
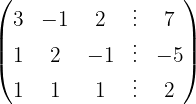
We apply the Gauss method
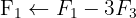
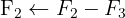

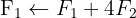

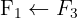
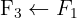

The system is consistent and determined

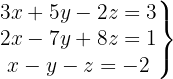
We write in matrix form
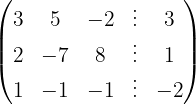
We apply the Gauss method
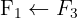
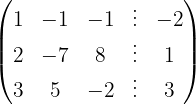
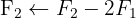

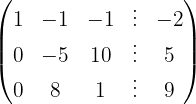
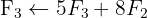

The system is consistent and determined
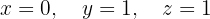
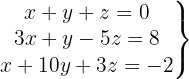
We write in matrix form
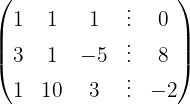
We apply the Gauss method
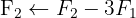
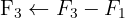
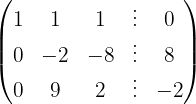
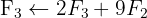
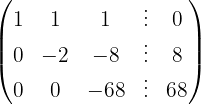
The system is consistent and determined
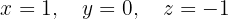
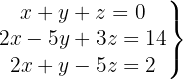
We write in matrix form
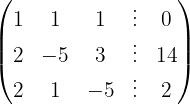
We apply the Gauss method
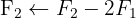
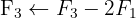
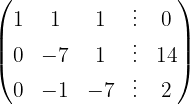
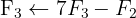
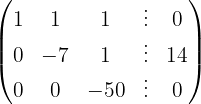
The system is consistent and determined
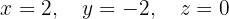
Verify if the Following System Is Determined or Indeterminate
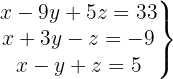
We write in matrix form

We apply the Gauss method
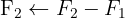
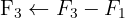

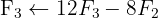

The system is consistent and indeterminate

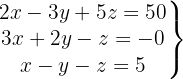
We write in matrix form

We apply the Gauss method

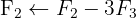

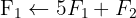

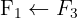
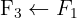

The system is consistent and determined

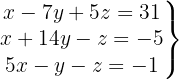
We write in matrix form

We apply the Gauss method
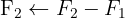
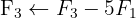

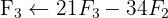
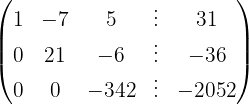
The system is consistent and determined
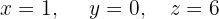
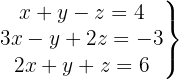
We write in matrix form
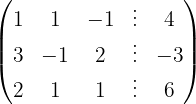
We apply the Gauss method
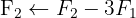
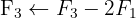
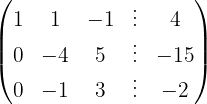
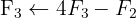
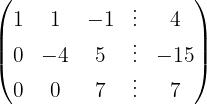
The system is consistent and determined
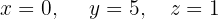
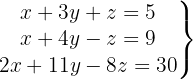
We write in matrix form

We apply the Gauss method
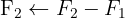
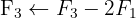
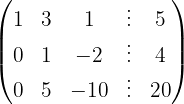
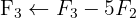
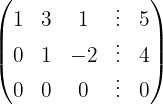
The system is consistent and indeterminate
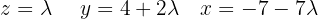
System of 4 Equations with 4 Variables
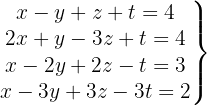
We write in matrix form

We apply the Gauss method
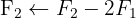
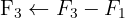
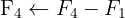
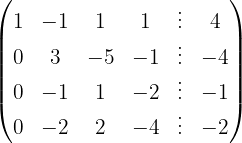
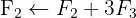


The system is consistent and indeterminate
We have that the system is underdetermined since the last row was canceled. We will parameterize the solution using  . The second equation becomes:
. The second equation becomes: 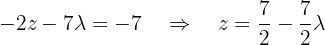
From here we proceed to express  in terms of
in terms of 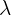 using the third equation, which becomes:
using the third equation, which becomes: 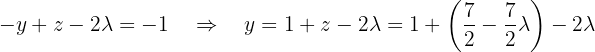

Finally, we use the first equation to express  in terms of
in terms of 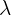 :
:
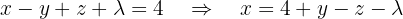
That is, 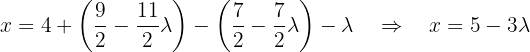
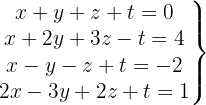
We write in matrix form

We apply the Gauss method
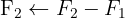
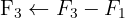
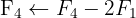

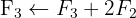


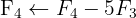

The system is consistent and determined

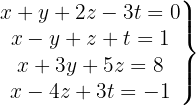
We write in matrix form

We apply the Gauss method
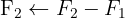
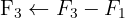
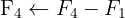


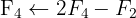

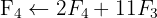

The system is consistent and determined
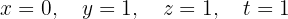
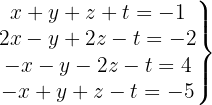
We write in matrix form
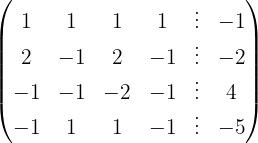
We apply the Gauss method
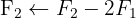
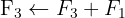
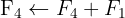

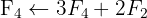

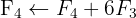

The system is consistent and determined

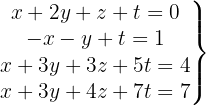
We write in matrix form
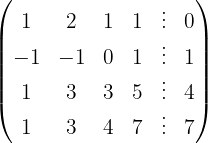
We apply the Gauss method
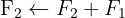
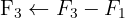
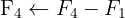

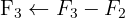




The system is consistent and indeterminate
We have that the system is underdetermined since the last row was canceled. We will parameterize the solution using  . The third equation becomes:
. The third equation becomes: 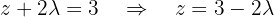
From here we proceed to express  in terms of
in terms of 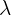 using the second equation, which becomes:
using the second equation, which becomes: 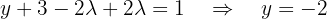 Finally, we use the first equation to express
Finally, we use the first equation to express  in terms of
in terms of 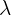 :
:
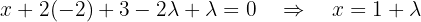
That is, 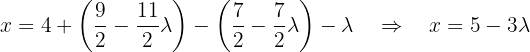
Verify the Indetermination of the System of 4 Equations
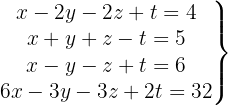
We write in matrix form

We apply the Gauss method
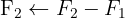
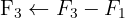
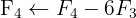




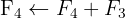

The system is consistent and indeterminate
We have that the system is underdetermined since the last row was canceled. We will parameterize the solution using 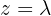 . The second equation becomes:
. The second equation becomes: 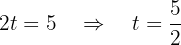
From here we proceed to express  in terms of
in terms of 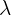 using the third equation, which becomes:
using the third equation, which becomes: 
Finally, we use the first equation to express  in terms of
in terms of 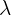 :
: 
Thus 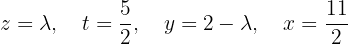
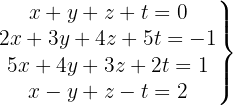
We write in matrix form
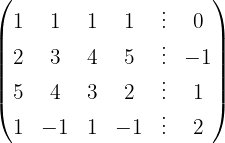
We apply the Gauss method
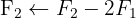
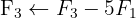

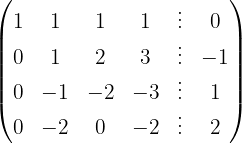


The system is consistent and indeterminate
We have that the system is underdetermined since the third row was canceled. We will parameterize the solution using  . The second equation becomes:
. The second equation becomes: 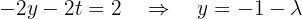
From here we proceed to express  in terms of
in terms of 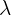 using the third equation, which becomes:
using the third equation, which becomes: 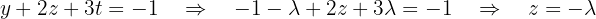
Finally, we use the first equation to express  in terms of
in terms of 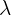 :
: 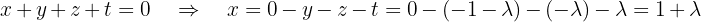
Thus 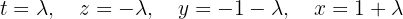
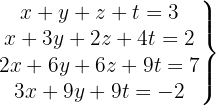
We write in matrix form

We apply the Gauss method
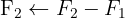
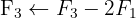
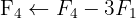


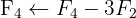

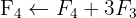

The system is inconsistent
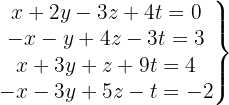
We write in matrix form

We apply the Gauss method
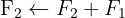
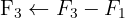
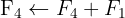
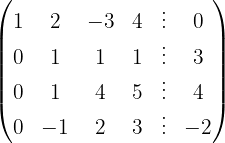
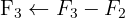
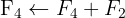
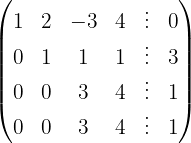


The system is consistent and indeterminate
We have that the system is underdetermined since the fourth row was canceled. We will parameterize the solution using  . The third equation becomes:
. The third equation becomes: 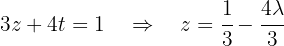
From here we proceed to express  in terms of
in terms of 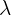 using the second equation, which becomes:
using the second equation, which becomes: 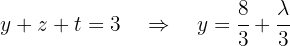
Finally, we use the first equation to express  in terms of
in terms of 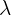 :
: 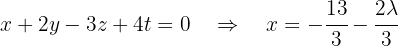
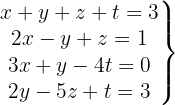
We write in matrix form

We apply the Gauss method
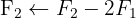

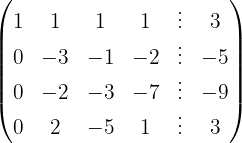
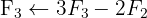
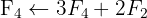
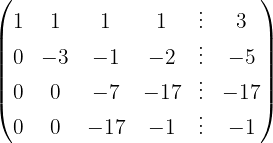
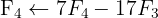
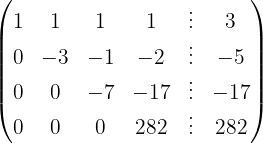
The system is consistent and determined
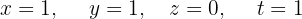
Solve the System of 3 Equations and 5 Variables
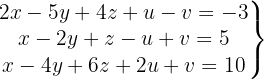
We write in matrix form
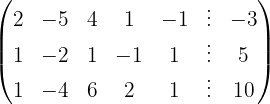
We apply the Gauss method
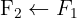
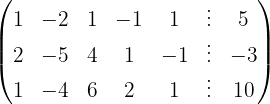
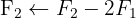
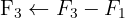
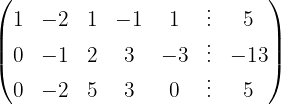

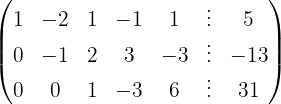
The system is consistent and determined
We will parameterize the solution using  . The third equation becomes:
. The third equation becomes: 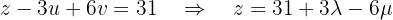
From here we proceed to express  in terms of
in terms of 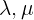 using the second equation, which becomes:
using the second equation, which becomes: 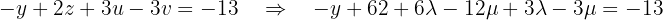
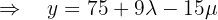
Finally, we use the first equation to express  in terms of
in terms of 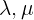 :
: 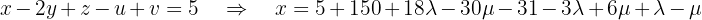

Thus 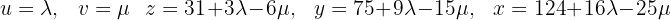
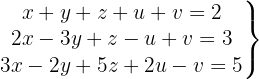
We write in matrix form
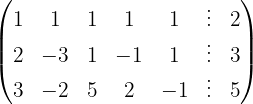
We apply the Gauss method
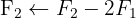

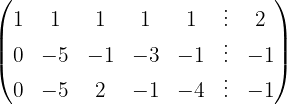
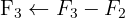
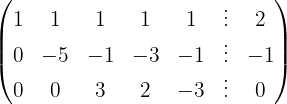
The system is consistent and indeterminate
We will parameterize the solution using  . The third equation becomes:
. The third equation becomes: 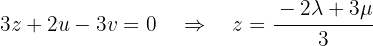
From here we proceed to express  in terms of
in terms of  using the second equation, which becomes:
using the second equation, which becomes: 

Finally, we use the first equation to express  in terms of
in terms of 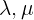 :
: 
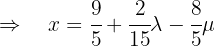
Thus 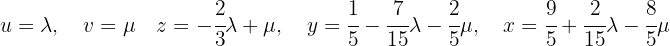
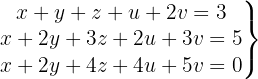
We write in matrix form
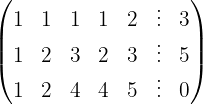
We apply the Gauss method
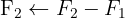
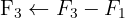
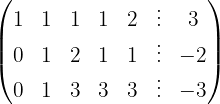
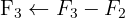

The system is consistent and indeterminate
We will parameterize the solution using  . From the third equation we obtain:
. From the third equation we obtain: 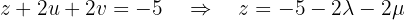
From here we proceed to express  in terms of
in terms of 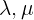 using the second equation, which becomes:
using the second equation, which becomes: 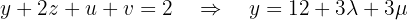
Finally, we use the first equation to express  in terms of
in terms of 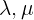 :
: 
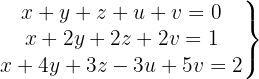
We write in matrix form
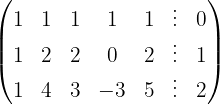
We apply the Gauss method
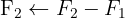
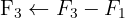
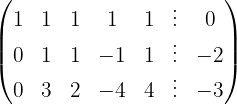
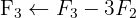
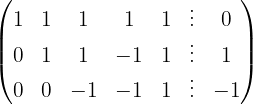
The system is consistent and indeterminate
We will parameterize the solution using  . From the third equation we obtain:
. From the third equation we obtain: 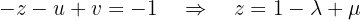
From here we proceed to express  in terms of
in terms of 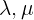 using the second equation, which becomes:
using the second equation, which becomes: 
Finally, we use the first equation to express  in terms of
in terms of 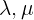 :
: 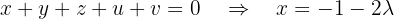
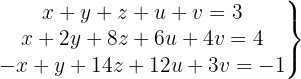
We write in matrix form
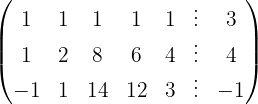
We apply the Gauss method
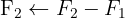
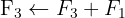
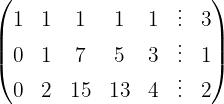

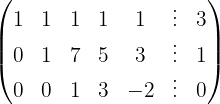
The system is consistent and indeterminate
We will parameterize the solution using  . From the third equation we obtain:
. From the third equation we obtain: 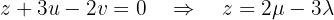
From here we proceed to express  in terms of
in terms of 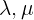 using the second equation, which becomes:
using the second equation, which becomes: 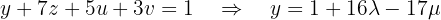
Finally, we use the first equation to express  in terms of
in terms of 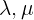 :
: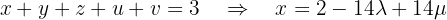
Solve the System of 4 Equations with 3 Variables
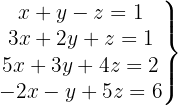
We write in matrix form

We apply the Gauss method
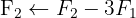
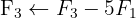
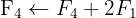


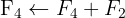
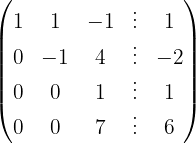

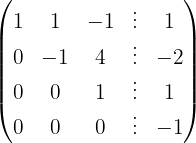
The system is inconsistent
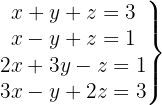
We write in matrix form
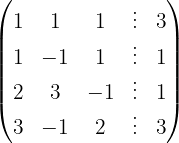
We apply the Gauss method
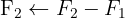
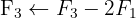
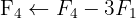
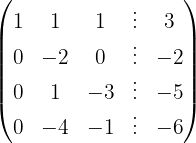



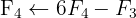

The system is consistent and determined
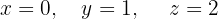
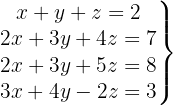
We write in matrix form

We apply the Gauss method
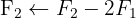
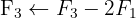
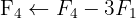
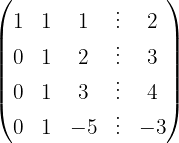
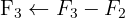


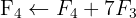
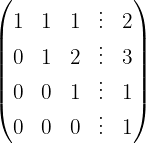
The system is inconsistent
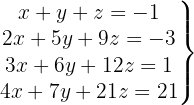
We write in matrix form

We apply the Gauss method
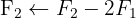

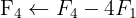
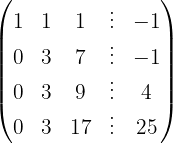
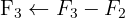


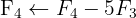

The system is inconsistent
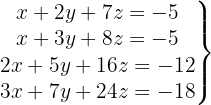
We write in matrix form

We apply the Gauss method
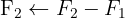
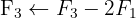
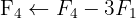

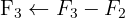




The system is inconsistent
Summarize with AI:












