
Greatest Common Divisor
The greatest common divisor, GCD, of two or more numbers is the largest number that divides all of them evenly.
Calculating the Greatest Common Divisor
1 Decompose all numbers into prime factors.
2 Take the common factors with the smallest exponent.
3 Multiply the common factors with the smallest exponent.
Example: Find the GCD of: 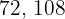 and
and 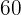 .
.
1 We decompose the numbers into prime factors

Thus, the numbers are written in the form

2 The common factors with the smallest exponent are 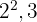
3 To calculate the GCD, we multiply the common factors with the smallest exponent
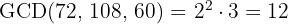
Note that if one number is a divisor of another, then it is the GCD of both.
Example: The number  is a divisor of
is a divisor of  , so
, so 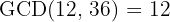
Least Common Multiple
The least common multiple, LCM, is the smallest of all common multiples of several numbers, excluding zero.
Calculating the Least Common Multiple
1 Decompose the numbers into prime factors.
2 Take the common and non-common factors with the largest exponent.
3 Multiply the common and non-common factors with the largest exponent.
Example: Find the LCM of: 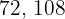 and
and 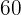 .
.
1 We decompose the numbers into prime factors

Thus, the numbers are written in the form

2 The common and non-common factors with the largest exponent are 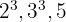
3 To calculate the LCM, we multiply the common and non-common factors with the largest exponent
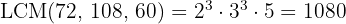
Thus,  is the smallest number that can be divided by
is the smallest number that can be divided by 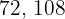 and
and 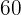 .
.
Note that if one number is a multiple of another, then it is the LCM of both.
Example: The number  is a multiple of
is a multiple of  , so
, so 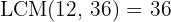
Relationship Between Greatest Common Divisor and Least Common Multiple
Since the greatest common divisor and the least common multiple are formed by the product of common factors with the smallest exponent and the product of common and non-common factors with the largest exponent, respectively, then
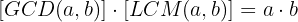
Practice Exercises
Calculate the 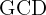 and
and 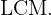 of
of  and
and 
1 We decompose the numbers into prime factors

Thus, the numbers are written in the form

2 The common factors with the smallest exponent are 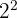
3 To calculate the GCD, we multiply the common factors with the smallest exponent
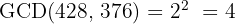
4 The common and non-common factors with the largest exponent are 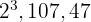
5 To calculate the LCM, we multiply the common and non-common factors with the largest exponent
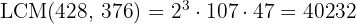
Calculate the 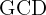 and
and 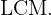 of
of  and
and 
1 We decompose the numbers into prime factors

Thus, the numbers are written in the form

2 The common factors with the smallest exponent are 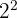
3 To calculate the GCD, we multiply the common factors with the smallest exponent
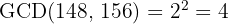
4 The common and non-common factors with the largest exponent are 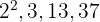
5 To calculate the LCM, we multiply the common and non-common factors with the largest exponent

Calculate the 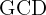 and
and 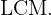 of
of  and
and 
1 We decompose the numbers into prime factors
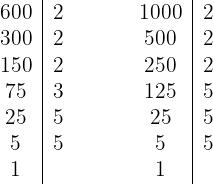
Thus, the numbers are written in the form
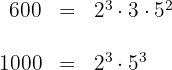
2 The common factors with the smallest exponent are 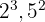
3 To calculate the GCD, we multiply the common factors with the smallest exponent
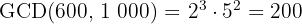
4 The common and non-common factors with the largest exponent are 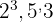
5 To calculate the LCM, we multiply the common and non-common factors with the largest exponent
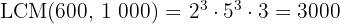
Calculate the 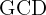 and
and 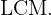 of
of  and
and 
1 We decompose the numbers into prime factors
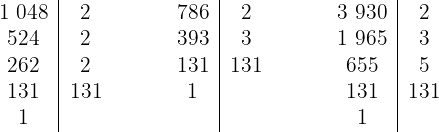
Thus, the numbers are written in the form

2 The common factors with the smallest exponent are 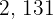
3 To calculate the GCD, we multiply the common factors with the smallest exponent
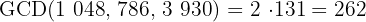
4 The common and non-common factors with the largest exponent are 
5 To calculate the LCM, we multiply the common and non-common factors with the largest exponent
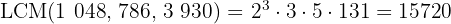
Calculate the 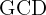 and
and 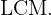 of
of 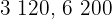 and
and 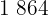
1 We decompose the numbers into prime factors
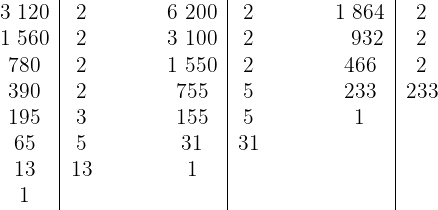
Thus, the numbers are written in the form

2 The common factors with the smallest exponent are 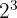
3 To calculate the GCD, we multiply the common factors with the smallest exponent
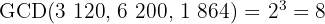
4 The common and non-common factors with the largest exponent are 
5 To calculate the LCM, we multiply the common and non-common factors with the largest exponent

A lighthouse turns on every  seconds, another every
seconds, another every  seconds, and a third every minute. At
seconds, and a third every minute. At  in the evening, all three coincide. At what time will they coincide again?
in the evening, all three coincide. At what time will they coincide again?
1 We decompose the numbers into prime factors
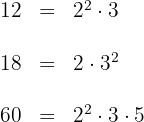
2 We calculate the LCM of the three numbers
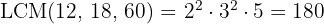
3 The lighthouses coincide every 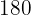 seconds, which is the same as
seconds, which is the same as  minutes; therefore, they coincide again at
minutes; therefore, they coincide again at 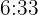 in the evening.
in the evening.
A traveler goes to Barcelona every  days and another every
days and another every  days. Today both have been in Barcelona. In how many days will both be in Barcelona at the same time again?
days. Today both have been in Barcelona. In how many days will both be in Barcelona at the same time again?
1 We decompose the numbers into prime factors
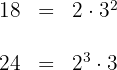
2 We calculate the LCM of the two numbers
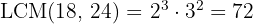
3 The two travelers will coincide again in  days.
days.
What is the smallest number that when divided separately by  and
and 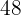 leaves a remainder of
leaves a remainder of  in each case?
in each case?
1 We decompose the numbers into prime factors

2 We calculate the LCM of the four numbers
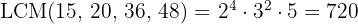
3 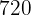 is the smallest number divisible by the four numbers, so if we want dividing by the four numbers to leave a remainder of
is the smallest number divisible by the four numbers, so if we want dividing by the four numbers to leave a remainder of  , then the number must be
, then the number must be 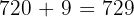 .
.
In a warehouse there are  wine barrels whose capacities are
wine barrels whose capacities are 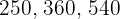 liters respectively. Their contents are to be bottled in a certain number of equal jugs. Calculate the maximum capacity of these jugs so that they can hold the wine contained in each of the barrels, and the number of jugs needed.
liters respectively. Their contents are to be bottled in a certain number of equal jugs. Calculate the maximum capacity of these jugs so that they can hold the wine contained in each of the barrels, and the number of jugs needed.
1 We decompose the numbers into prime factors
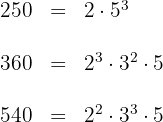
2 We calculate the GCD of the three numbers
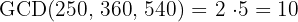
3 The capacity of each jug is  liters and the number of jugs is
liters and the number of jugs is  .
.
The floor of a room to be tiled is 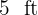 long and
long and 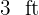 wide. Calculate the side in inches and the number of tiles, such that the number of tiles placed is minimum and it is not necessary to cut any of them.
wide. Calculate the side in inches and the number of tiles, such that the number of tiles placed is minimum and it is not necessary to cut any of them.
1 The floor of the room to be tiled has dimensions 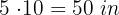 long and
long and 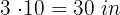 wide.
wide.
2 We calculate the GCD of the two numbers
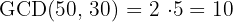
3 The side of each tile is 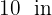 and
and  tiles are required lengthwise and
tiles are required lengthwise and  widthwise, so in total
widthwise, so in total 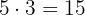 tiles are required.
tiles are required.
A merchant wants to pack  apples and
apples and  oranges in boxes, so that each box contains the same number of apples or oranges and, furthermore, the largest possible number. Find the number of oranges in each box and the number of boxes needed.
oranges in boxes, so that each box contains the same number of apples or oranges and, furthermore, the largest possible number. Find the number of oranges in each box and the number of boxes needed.
1 We calculate the GCD
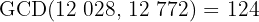
2 We calculate the number of boxes required
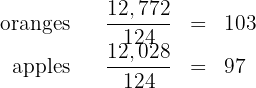
Thus, the number of boxes required is 
How large is the largest square tile that fits an exact number of times in a room 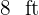 long and
long and 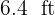 wide? And how many tiles are needed?
wide? And how many tiles are needed?
1 The floor of the room to be tiled has dimensions 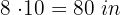 long and
long and 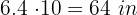 wide
wide
2 We calculate the GCD of the two numbers
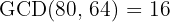
3 The side of each tile is 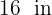 and
and 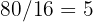 tiles are required lengthwise and
tiles are required lengthwise and 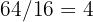 widthwise, so in total
widthwise, so in total  tiles are required.
tiles are required.
Summarize with AI:












