Chapters
Welcome to the Polynomial Exercises section for freshman students!
In this set of exercises, we will explore the world of polynomials, which are algebraic expressions formed by the sum or difference of terms called monomials. Polynomials are fundamental tools in algebra and have various applications in solving mathematical problems and representing phenomena in science.
Throughout these exercises, we will address key concepts such as identifying like terms, adding and subtracting polynomials, multiplying polynomials and, in some cases, factorization and division. These exercises are designed to strengthen your understanding of polynomials and improve your skills in algebraic manipulation.
We hope you enjoy tackling these challenges and that you find the practice you need to consolidate your knowledge in the exciting world of polynomials. Let's dive into solving exercises and explore the properties and operations of these expressive algebraic objects!
Identifying Monomials
Indicate which of the following expressions are monomials. If affirmative, indicate its degree and coefficient.
1 
2 
3 
4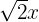 
5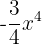 
6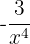 
7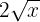 
8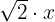 
9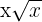 
10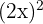 
1
Yes, it is a monomial; degree 3 and coefficient 3.
2
It is not a monomial, because the exponent is not a natural number.
3
It is not a monomial, because a sum appears.
4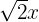
Yes, it is a monomial; degree 1 and coefficient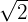 
.
5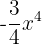
Yes, it is a monomial; degree 4 and coefficient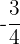 
.
6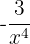
It is not a monomial, it does not have a natural exponent.
7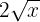
It is not a monomial, because the literal part is inside a root.
8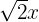
Yes, it is a monomial; degree 1 and coefficient .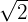
9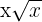
It is not a monomial, because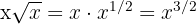 
, which is a non-natural exponent.
10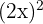 
Yes, it is a monomial; of degree 2 and coefficient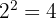 
.
Operations with Monomials
Perform the following operations with monomials:
1 
2 
3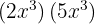 
4 
5 
6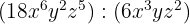 
7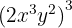 
8 
9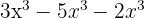 
10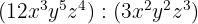 
11 
12 
13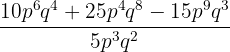 
14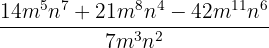 
15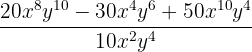 
1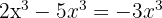 
2 
3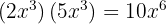 
4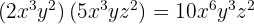 
5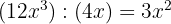 
6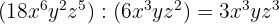 
7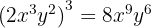 
8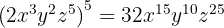 
9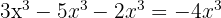 
10 
11 
12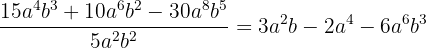
13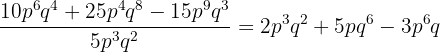
14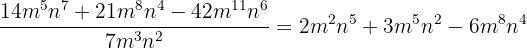
15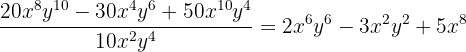
Identifying Polynomials
Indicate whether the following algebraic expressions are polynomials or not. If affirmative, indicate what its degree and independent term are.
1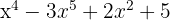 
2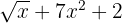 
3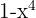 
4 
5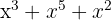 
6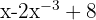 
7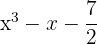 
8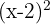 
9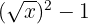 
10 
1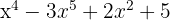
Yes, it is a polynomial; degree 5 and independent term 5
2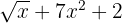
It is not a polynomial, because the literal part of the first monomial is inside a root.
3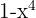
Yes, it is a polynomial; degree 4 and independent term 1
4
It is not a polynomial, because the exponent of the first monomial is not a natural number.
5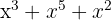
Yes, it is a polynomial; degree 5 and independent term 0
6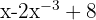
It is not a polynomial, because the exponent of the second monomial is not a natural number.
7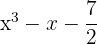
Yes, it is a polynomial; degree 3 and independent term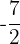 
8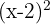
Yes, it is a polynomial; degree 2 and independent term 
9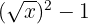
Yes, it is a polynomial; degree 1 and independent term 
10
It is not a polynomial, because the exponent is not a natural number.
Writing in Mathematical Language
Write:
1 A ordered polynomial without an independent term.
2 A non-ordered and complete polynomial.
3 A complete polynomial without an independent term.
4 A polynomial of degree 4, complete and with odd coefficients.
5 A polynomial of degree 2, complete and with negative coefficients.
1 A ordered polynomial without an independent term.
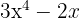
2 A non-ordered and complete polynomial.
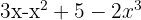
3 A complete polynomial without an independent term.
Impossible
4 A polynomial of degree 4, complete and with odd coefficients.
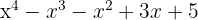
5 A polynomial of degree 2, complete and with negative coefficients.
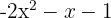
Calculation with Polynomials
Given the polynomials:
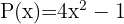
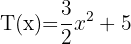
Calculate:
1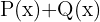
2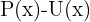
3
4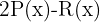
5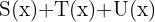
6
7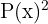
8
9
10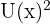
1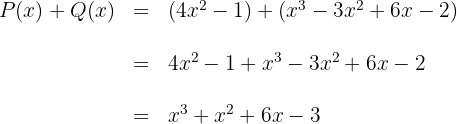
2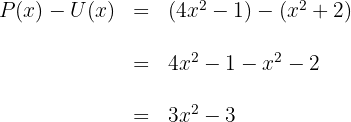
3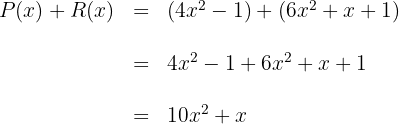
4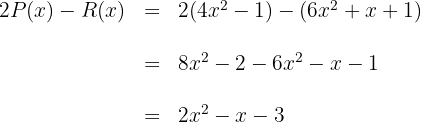
5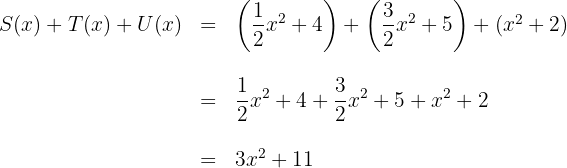
6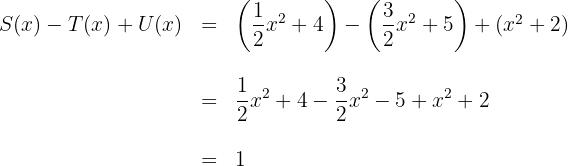
7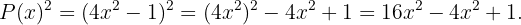
8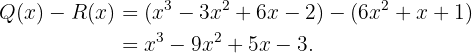
9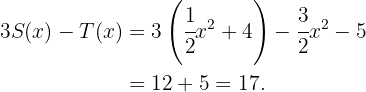
10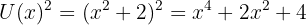
Multiplications
Multiplicate:
1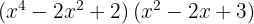
2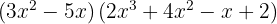
3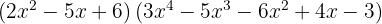
4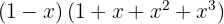
5
1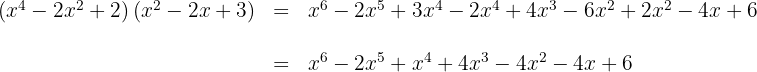
2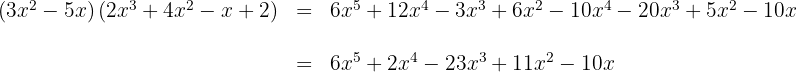
3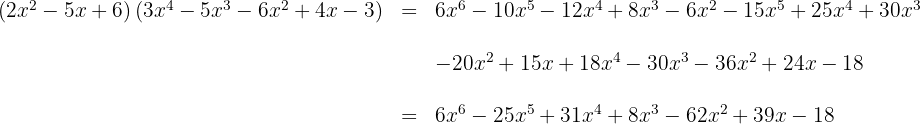
4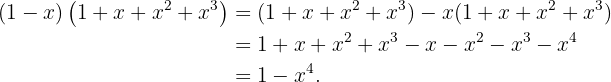
5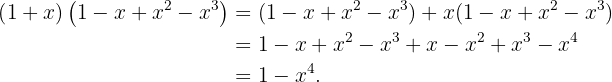
Finding the Numerical Value of the Polynomial
Find the numerical value of the polynomial 
, for:
1
.
2
.
3
.
4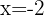
.
5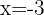
.
1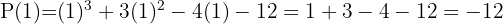
2
3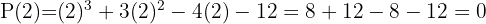
4
5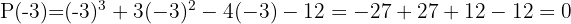
Calculation
Calculate:
1
2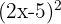
3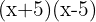
4
5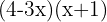
1
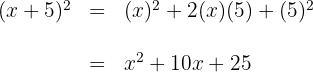
2
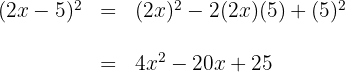
3
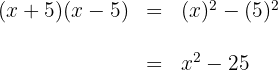
4
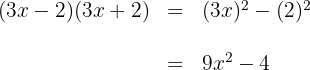
5
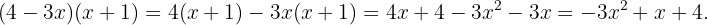
Division of Polynomials
Divide:
1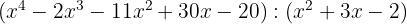
2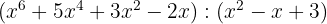
3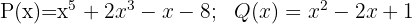
4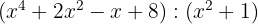
5
1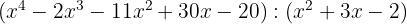
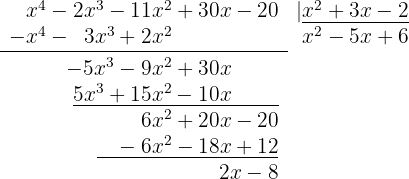
Quotient 
; Remainder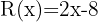 
2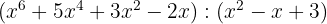
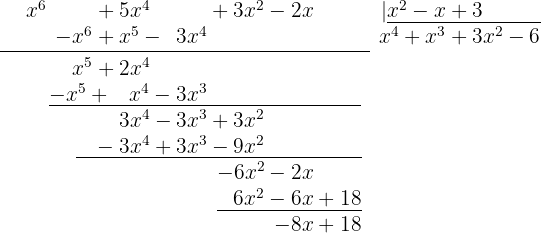
Quotient 
; Remainder 
3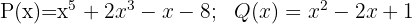
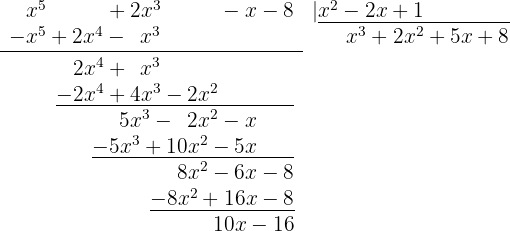
Quotient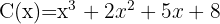 
; Remainder 
4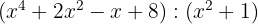
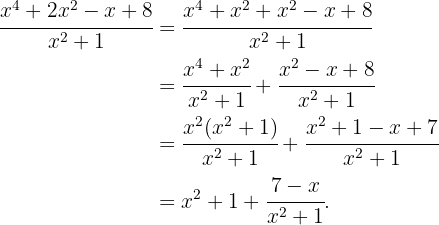
5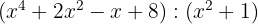
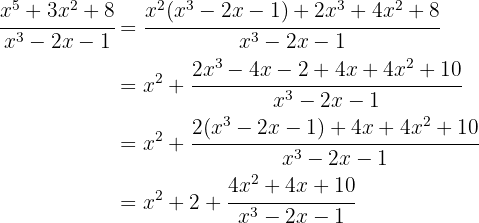
Division by Ruffini
Divide by Ruffini:
1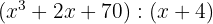
2
3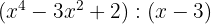
4
5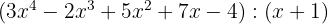
1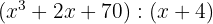
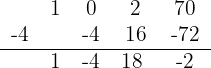
So the quotient and remainder are:
Quotient 
; Remainder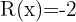 
2
So the quotient and remainder are:
Quotient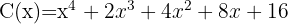 
; Remainder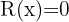 
3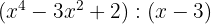
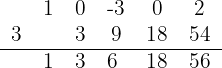
So the quotient and remainder are:
Quotient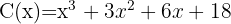 
; Remainder 
4
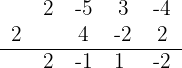
So the quotient and remainder are:
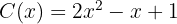with a remainder of -2.
5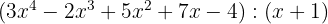
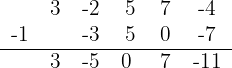
So the quotient and remainder are:
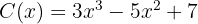with a remainder of -11.
Did you like this article? Rate it!
Loading...
