Welcome to our blog dedicated to the fascinating and powerful mathematical technique known as "integration by parts". Integrals are a fundamental part of calculus, and on many occasions, they can be challenging to tackle. However, don't be afraid! We are here to unravel the mystery behind integration by parts and facilitate its understanding.
From physics to engineering, through various areas of knowledge, functions that must be integrated using integration by parts constantly appear. In this article, we present you with a wide variety of solved exercises that will help you understand and perfect this important technique in mathematics.
Join us and become a master of integration by parts!
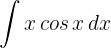
1 We choose 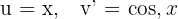 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
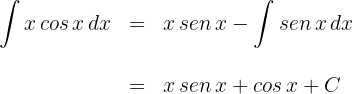
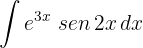
1 We choose 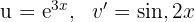 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
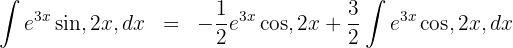
3 The last integral obtained is solved by integration by parts, so we choose 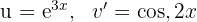 and calculate
and calculate  and
and 

4 We substitute the values of  and
and  into the integration by parts formula and obtain
into the integration by parts formula and obtain
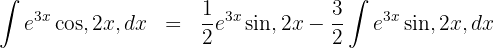
5 We substitute the result obtained from step 4 into the result from step 2 and solve the resulting equation

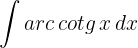
1 We choose 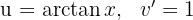 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
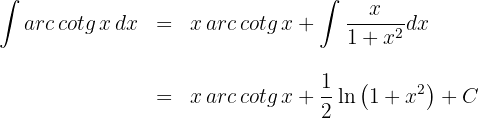
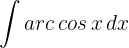
1 We choose 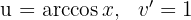 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula

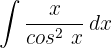
1 We choose 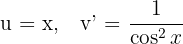 and calculate
and calculate  and
and 
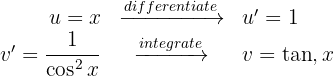
2 We substitute the values of  and
and  into the integration by parts formula considering
into the integration by parts formula considering 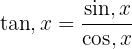
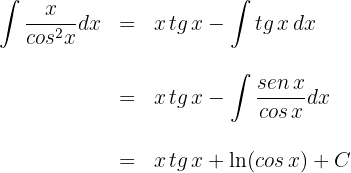

1 We choose 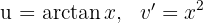 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
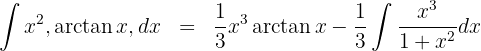
3 We perform the division of the new integrand and obtain 
4 We substitute into the integral and solve


1 We choose 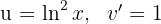 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
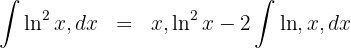
3 The last integral obtained is solved by integration by parts, so we choose 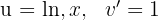 and calculate
and calculate  and
and 

4 We substitute the values of  and
and  into the integration by parts formula and obtain
into the integration by parts formula and obtain
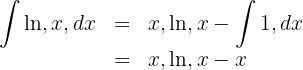
5 We substitute the result obtained from step 4 into the result from step 2


1 We choose 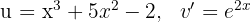 and calculate
and calculate  and
and 
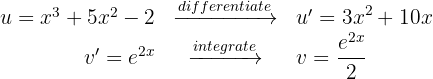
2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
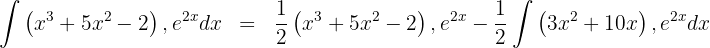
3 The last integral obtained is solved by integration by parts, so we choose 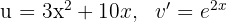 and calculate
and calculate  and
and 
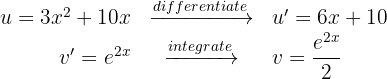
4 We substitute the values of  and
and  into the integration by parts formula and obtain
into the integration by parts formula and obtain
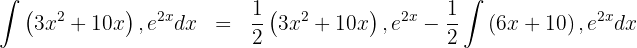
5 The last integral obtained is solved by integration by parts, so we choose 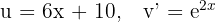 and calculate
and calculate  and
and 
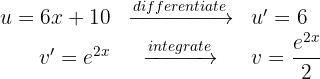
6 We substitute the values of  and
and  into the integration by parts formula and obtain
into the integration by parts formula and obtain
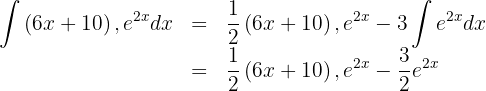
7 We substitute the result obtained from step 6 into the result from step 4
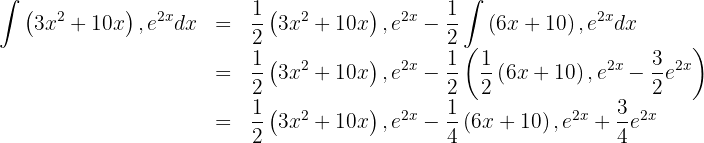
8 We substitute the result obtained from step 7 into the result from step 2
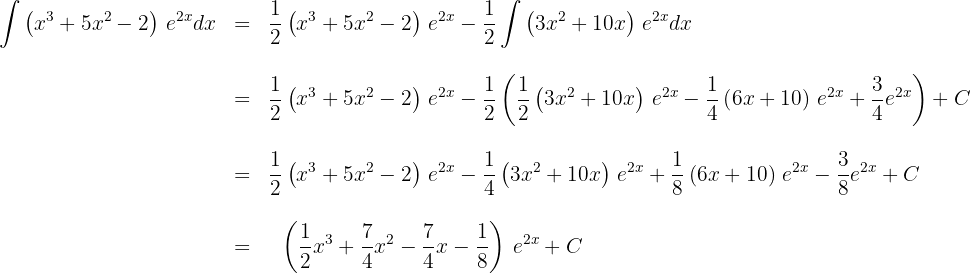
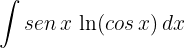
1 We choose 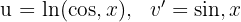 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
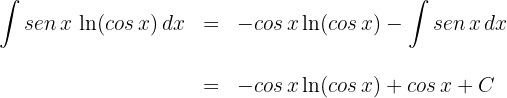
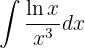
1 We choose  and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
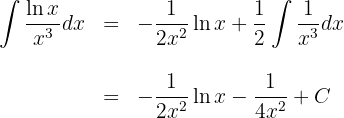
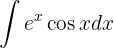
1 We choose 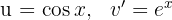 and calculate
and calculate  and
and 
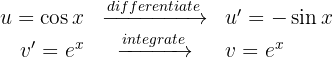
2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
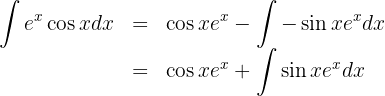
3 The last integral obtained is solved by integration by parts, so we choose 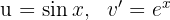 and calculate
and calculate  and
and 
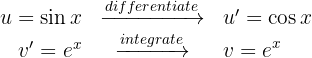
4 We substitute the values of  and
and  into the integration by parts formula and obtain
into the integration by parts formula and obtain
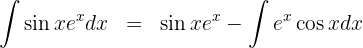
5 We substitute the result obtained from step 4 into the result from step 2 and solve the resulting equation

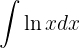
1 We choose 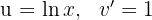 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
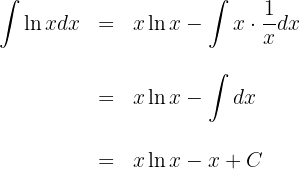
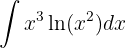
1 We choose 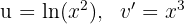 and calculate
and calculate  and
and 

2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula


1 We choose 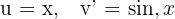 and calculate
and calculate  and
and 
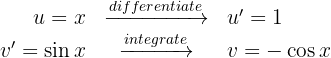
2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula


1 We choose 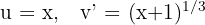 and calculate
and calculate  and
and 
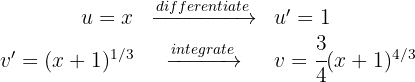
2 We substitute the values of  and
and  into the integration by parts formula
into the integration by parts formula
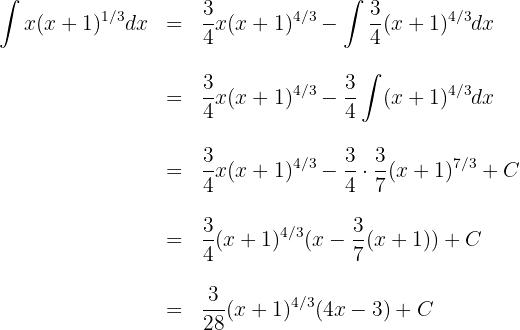
Summarize with AI:


