Chapters
Substitution Method
The integration method by substitution or change of variable is based on the derivative of the composite function.
To change variables we identify a part of what is to be integrated with a new variable t, so that a simpler integral is obtained.
Steps to Integrate by Change of Variable
1 Make the change of variable and differentiate both terms:
2 Substitute the differential in the integral:
3 If the resulting integral is simpler, we integrate:
4 Return to the initial variable:
Example: Solve this integral using integration by change of variable:
1 We perform the change of variable
We calculate the differential
2 We substitute in the integral and simplify the integrand
3 We solve the new integral
4 We return to the initial variable, for this we use 
Thus the desired solution is
Common Variable Changes
Below we list some of the variable changes used to solve integrals:
1 
2 
3 
4 
5 In rational functions of radicals with different indices, of the same linear radicand 
, the change of variable is 
raised to the least common multiple of the indices.
6 If 
is even: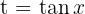 
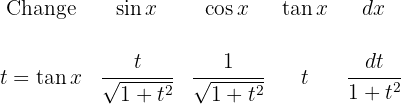
7 If 
is not even:
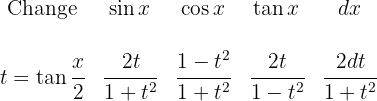
Proposed Exercises
Solve the following integrals, using the substitution method:
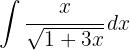
1 We perform the change of variable
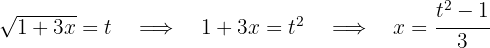
We calculate the differential
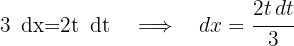
2 We substitute in the integral and simplify the integrand
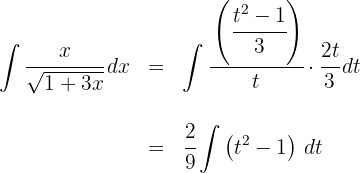
3 We solve the new integral
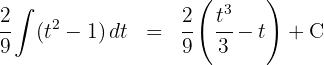
4 We return to the initial variable, for this we use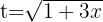 
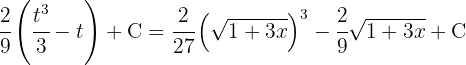
Thus the desired solution is
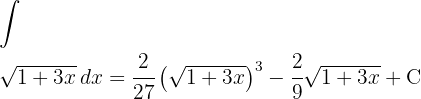
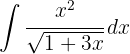
1 We perform the change of variable
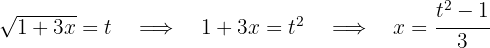
We calculate the differential
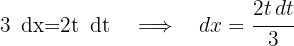
2 We substitute in the integral and simplify the integrand
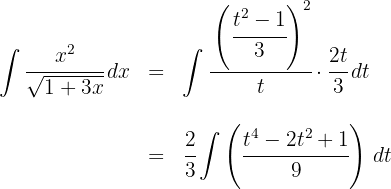
3 We solve the new integral
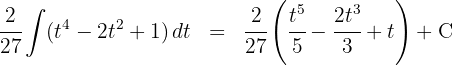
4 We return to the initial variable, for this we use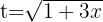
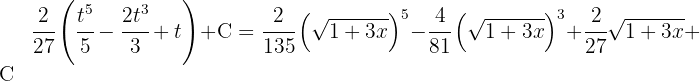
Thus the desired solution is
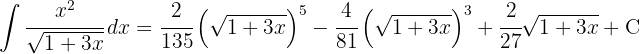
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and to simplify we implement trigonometric identities
3 We solve the integral we obtained
4 We return to the initial variable, for this we solve for in the initial variable change
We calculate for the sine and cosine of
Thus, the result is expressed in variable 
as
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
3 We solve the integral we obtained
4 We return to the initial variable
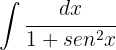
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
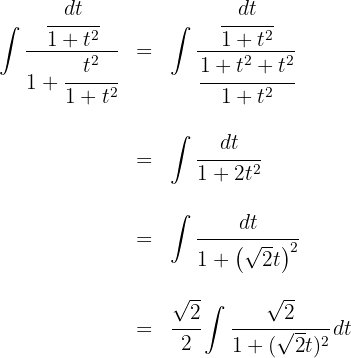
3 We solve the integral we obtained
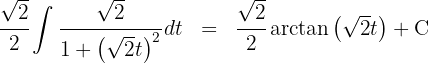
4 We return to the initial variable
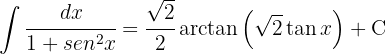
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
3 We solve the integral we obtained
4 We return to the initial variable
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
3 We solve the integral we obtained
4 We return to the initial variable
Thus, the solution in terms of the initial variable is
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
3 We solve the integral we obtained
4 We return to the initial variable
Thus, the solution in terms of the initial variable is
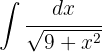
1 We perform the change of variable and we calculate the differential
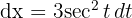
2 We substitute in the integral and we simplify
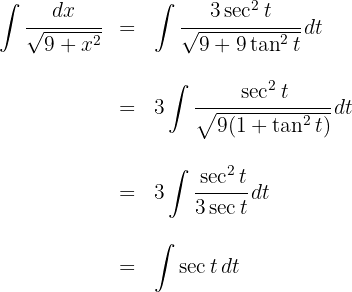
3 We solve the integrals we obtained
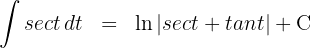
4 We return to the initial variable
Thus, the solution in terms of the initial variable is
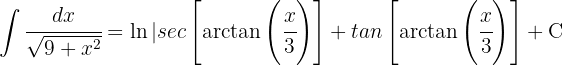
1 We perform the change of variable and we calculate the differential
2 We substitute in the integral and we simplify
3 We solve the integrals we obtained
4 We return to the initial variable
Thus, the solution in terms of the initial variable is
Did you like this article? Rate it!
Loading...
