Chapters
Definition of the Inverse of a Matrix
A square matrix 
is said to be invertible if there exists a matrix 
with the property that 
where 
is the identity matrix.
The matrix is unique, we call it the inverse of and denote it by 
That is,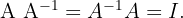 
Important observation: A matrix is invertible if and only if its determinant is different from zero. That is, a matrix has an inverse if its determinant is non-zero.
Properties of the Inverse Matrix
The inverse of a matrix satisfies the following properties:
1 Let and be invertible matrices of the same order, then the product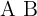 
is invertible and furthermore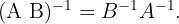 
2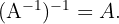 
3 Let 
be a non-zero real number, then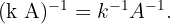 
4 If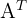 
denotes the transpose of a matrix, then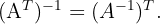 
- The inverse matrix is an important tool in solving systems of linear equations since any system can be written in the form
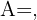where is the coefficient matrix of the system, 
is the column matrix or column vector that contains the "unknown" variables and 
is the column matrix whose entries are the constants on the right side of the equations in the system. For example, the system
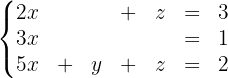
can be expressed as the matrix equation 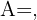where
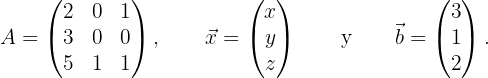
Since the coefficient matrix is square, it may be invertible.
If is invertible and we have a way to calculate its inverse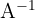 
, then we can determine by simply a matrix multiplication: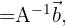
since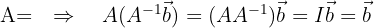 
solving the system of equations.
Thus, a good application of the inverse of a matrix is the efficient solution of systems of linear equations.
Let's recall that, the transpose matrix of a matrix is denoted by 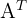and is obtained by exchanging its rows for columns (or vice versa).
For example, continuing with the matrix from above we have that, if
The inverse matrix can be calculated by two methods: by the Gauss method and by the adjoint method. In the latter is where the transpose matrix appears. Thus, the main practical application of the transpose matrix is the calculation of the inverse matrix.
We have already studied the Gauss method in another article, now we will focus our attention on the adjoint method.
Calculation by the Adjoint Method
The calculation of an inverse matrix by the adjoint method is based on the following result:
Where
To understand the procedure, let's look at an example:
Example: Calculate the inverse of the matrix
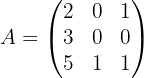
which corresponds to the coefficients of the system of linear equations from above.
Solution:
To calculate the inverse we must follow these steps:
1 We calculate the determinant of the matrix:
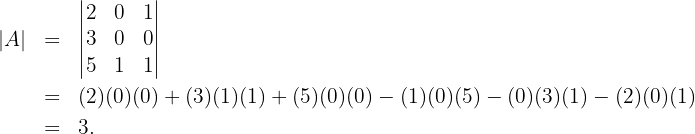
Since the determinant is not zero, the matrix has an inverse.
2 We find the adjoint matrix: This is the one in which each element is replaced by its adjoint.
That is,
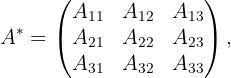
where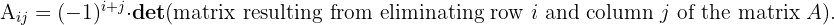 
Thus
Therefore we have that
3 We calculate the transpose of the adjoint matrix: If
4 The inverse matrix equals the transpose of the adjoint matrix divided by the determinant of the original matrix: That is,
Therefore
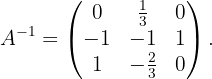
Thus, we have obtained the inverse of the matrix .
Observation: As a final comment, we can solve the previously stated system of linear equations by doing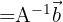
obtaining that
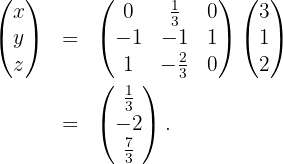
Then, the choice of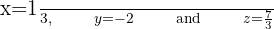 
solves the previously stated system, as can be easily verified.
Did you like this article? Rate it!
Loading...
