
What Are Linear Equations?
Linear equations or first-degree equations are of the type 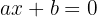 , with
, with 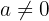 , or any other equation that, when operated on, transposed, and simplified, adopts this expression.
, or any other equation that, when operated on, transposed, and simplified, adopts this expression.
Steps to Solve a Linear Equation
In general, to solve a linear equation or first-degree equation we must follow these steps:
1 Remove parentheses
That is, if there are expressions like
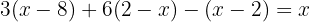
Then we expand using the distributive property, which is 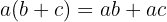 , and the law of signs will also be important.
, and the law of signs will also be important.
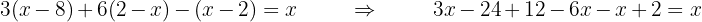
2 Remove denominators
In case there are fractional terms in the expression, we must identify the different denominators present, calculate the least common multiple (LCM) of these, and multiply the equation by the LCM. Instead of the LCM, you can also calculate the product of all denominators, although the first method is more recommended since it gives a smaller or more simplified number. For example:
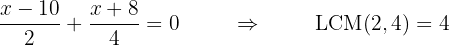
We multiply the first fraction by 
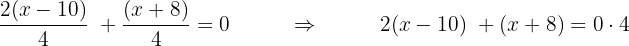
Here again we might need to remove parentheses to simplify

3 Group the terms with x on one side and the independent terms on the other
Once we have completed step 1 and step 2, we will have the sum and subtraction of terms with x and independent terms on both sides of the equation. What follows is to gather the  terms on one side and the independent terms on the other. For this, remember that if a
terms on one side and the independent terms on the other. For this, remember that if a 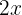 is being added on one side of the equation, for example, I can move it to the other side with the inverse operation, that is, it would become
is being added on one side of the equation, for example, I can move it to the other side with the inverse operation, that is, it would become 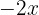 on the other side.
on the other side.
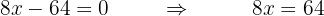
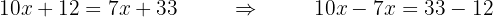
4 Combine like terms
Now that we have terms with  together, we add or subtract them depending on the case. Similarly with the independent terms, for example:
together, we add or subtract them depending on the case. Similarly with the independent terms, for example:

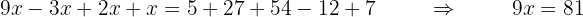
5 Solve for the unknown
If there is a coefficient accompanying the variable  , since it is multiplying, we will move it to the other side with the inverse operation, that is, dividing. This is what we call solving for the variable.
, since it is multiplying, we will move it to the other side with the inverse operation, that is, dividing. This is what we call solving for the variable.
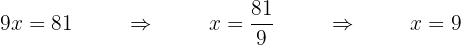
Linear Equation Exercises

We solve for the unknown by dividing both sides by  . Also, as a practical method, we can say that the
. Also, as a practical method, we can say that the  that is multiplying on the first side moves to the second side as a divisor.
that is multiplying on the first side moves to the second side as a divisor.


We group like terms by adding  and
and  to both sides, obtaining an equivalent equation.
to both sides, obtaining an equivalent equation.
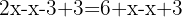
In practice, we usually say that if a term is adding  on one side, it moves to the other side subtracting
on one side, it moves to the other side subtracting  , and if it was subtracting
, and if it was subtracting  , it moves to the other side adding
, it moves to the other side adding  . We add:
. We add:



We use the distributive property to operate on the parentheses, that is, multiply each algebraic term inside the parentheses by  . Thus, on the left side we have:
. Thus, on the left side we have: 
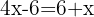
We group like terms; the x that is adding moves to the other side subtracting, and the  that is subtracting moves to the other side adding. We add:
that is subtracting moves to the other side adding. We add:

We solve for the unknown; the  that is multiplying moves to the other side dividing:
that is multiplying moves to the other side dividing:

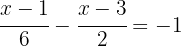
To remove the denominators, we need to find the least common multiple of  and
and 
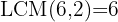
We multiply both sides of the equation by the LCM, in this case  , and obtain:
, and obtain:
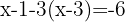
We multiply using the distributive property to solve the parentheses, group and add like terms:
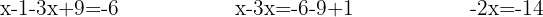
We solve for the unknown:
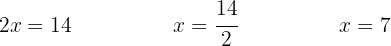
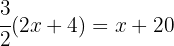
We multiply  by each term inside the parentheses (distributive property) to solve the parentheses and simplify:
by each term inside the parentheses (distributive property) to solve the parentheses and simplify:

We group and add like terms:
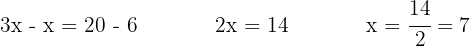
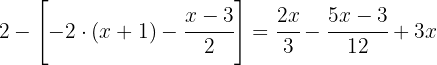
In this case it's convenient to first develop the operation 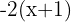 . When solving it, we can change the bracket to a parenthesis.
. When solving it, we can change the bracket to a parenthesis.
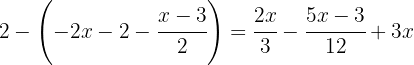
We operate the terms inside the parentheses by −1 to remove the negative sign and the parentheses from the equation:
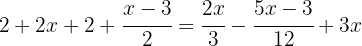
To remove the denominators, we need to find the least common multiple of 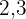 and
and  .
.
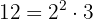
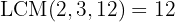
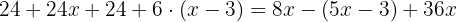
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and the second by
and the second by  :
:
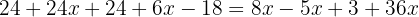
We group like terms:
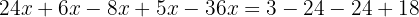
We add:

We divide both sides by: 
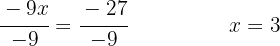

Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and the second by
and the second by  .
.
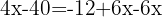
We group like terms:
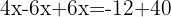
We add like terms and solve:


Using the distributive property to solve the parentheses, we multiply the first parenthesis by  and the second by
and the second by  .
.

We group like terms:
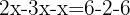
We add like terms and solve:

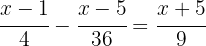
To remove the denominators, we need to find the least common multiple of  ,
,  and
and 
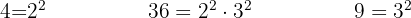
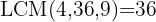
We divide the common denominator by each denominator and multiply the result by the corresponding numerator:
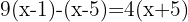
Using the distributive property to operate on the parentheses, we multiply the first by  , the second by
, the second by  and the third by
and the third by  .
.
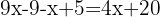
We group like terms:

We add like terms and solve:

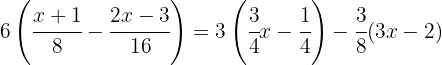
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  , the second by
, the second by  and the third by
and the third by  .
.
It's necessary to remember that when we multiply a whole number by a fraction, we solve it by multiplying the whole number by the numerator of the fraction and the denominator remains the same.
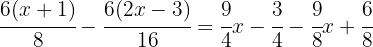
We apply the distributive property to develop the parentheses in the numerators:
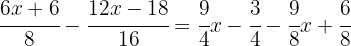
To remove the denominators, we need to find the least common multiple of  ,
,  and
and  .
.
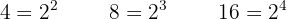
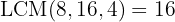
We divide the common denominator by each denominator and multiply the result by the corresponding numerator.
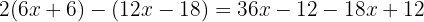
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and simplify carefully with attention to sign changes.
and simplify carefully with attention to sign changes.

We group like terms:
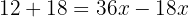
We solve for the unknown:
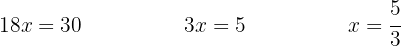
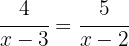
For the equality between the two fractions to hold, the product of the extremes must equal the product of the means.
Or if preferred, we can also find the LCM which is 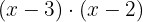 because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator.
because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator.
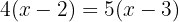
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and the second by
and the second by  .
.
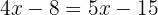
We group like terms:

We solve for the unknown:
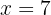
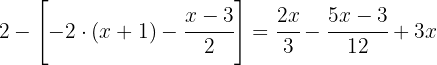
In this case it's convenient to first develop the operation 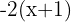 . When solving it, we can change the bracket to a parenthesis.
. When solving it, we can change the bracket to a parenthesis.
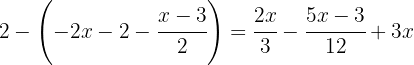
We operate the terms inside the parentheses by −1 to remove the negative sign and the parentheses from the equation:
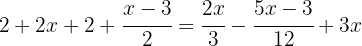
To remove the denominators, we need to find the least common multiple of 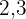 and
and  .
.
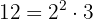
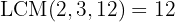
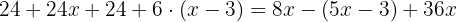
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and the second by
and the second by  :
:
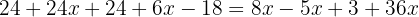
We group like terms:
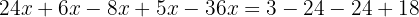
We add:

We divide both sides by: 
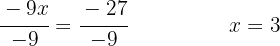
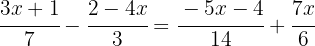
To remove the denominators, we need to find the least common multiple of  ,
,  ,
,  and
and  .
.

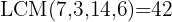
We divide the common denominator by each denominator and multiply the result by the corresponding numerator:

Using the distributive property to develop the parentheses, we multiply the first parenthesis by  , the second by
, the second by 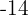 , and the third by
, and the third by  .
.
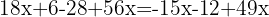
We group like terms:

We add like terms and solve:
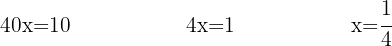
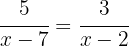
For the equality between the two fractions to hold, the product of the extremes must equal the product of the means.
Or if preferred, we can also find the LCM which is 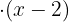 because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator.
because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator.
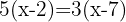
Using the distributive property to develop the parentheses, we multiply the first parenthesis by  and the second by
and the second by  .
.
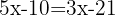
We add like terms:
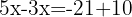
We solve for the unknown:

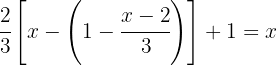
We operate the terms inside the parentheses by  to remove the negative sign and the parentheses from the equation; now we can substitute the bracket with a parenthesis.
to remove the negative sign and the parentheses from the equation; now we can substitute the bracket with a parenthesis.
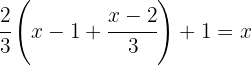
We use the distributive property to develop the parentheses.
It's necessary to remember that when we multiply one fraction by another, we must multiply numerator by numerator and denominator by denominator.
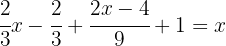
To remove the denominators, we need to find the least common multiple of  and
and  .
.

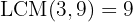

We group like terms:

We add and solve:

Still struggling? At Superprof we can help you find the best math course for you!












