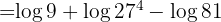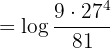Definition of Logarithms
You have surely already studied powers and know that, for example:
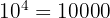
But suppose you want to find a power to which to raise the number 10 so that the result is 10,000,000. That can be written as follows:
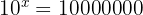
Could you solve for the letter ' ' in that equation?
' in that equation?
The equation we wrote is an exponential equation. To be able to solve for the variable ' ' we need to use a logarithm. A logarithm is an "operation" or "function" that returns the power to which you must raise a given base to obtain a desired result. In our example, the base is 10 and the desired result is 10000000, so we can write:
' we need to use a logarithm. A logarithm is an "operation" or "function" that returns the power to which you must raise a given base to obtain a desired result. In our example, the base is 10 and the desired result is 10000000, so we can write:
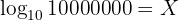
In general, we can express logarithmic notation as follows:
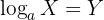
Where:
a is the base
x is the desired result (also known as the argument)
y is the power to which base a is raised
Below, we show you some examples of expressions in exponential notation and logarithmic notation:
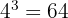

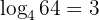
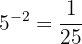

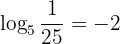


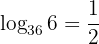
It should be noted that the most commonly used bases in logarithms are  y
y  (Euler's number,
(Euler's number, 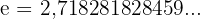 )
)
When we use base  it is not necessary to write the base of the logarithm:
it is not necessary to write the base of the logarithm:
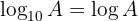
The logarithm with base  is known as the Napierian logarithm (or natural logarithm) and is represented as:
is known as the Napierian logarithm (or natural logarithm) and is represented as:

Properties of Logarithms
1 The logarithm of a product equals the sum of the logarithms of the factors
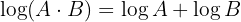
2 The logarithm of a quotient equals the difference of the logarithm of the dividend and the logarithm of the divisor
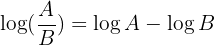
3 The logarithm of a power equals the product of the exponent times the logarithm of the base
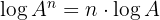
4 The logarithm of a root equals the quotient between the logarithm of the radicand and the index of the root
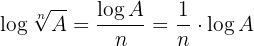
From properties  and
and  we can deduce that:
we can deduce that:

5 The logarithm base ' ' of '
' of ' ' is '
' is ' '
'
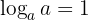
6 The logarithm of  is
is  (regardless of the logarithm base)
(regardless of the logarithm base)
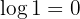
Thus:
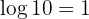
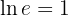
7 The argument of a logarithm must always be greater than zero
For  it holds that
it holds that 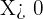
Use of Logarithm Properties
Base Changes
To write a logarithm of base ' ' in an equivalent expression with logarithm of base '
' in an equivalent expression with logarithm of base ' ' we can do the following:
' we can do the following:
Let
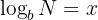
We can rewrite the expression in its exponential notation as:
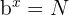
Applying 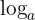 on both sides of the equality:
on both sides of the equality:
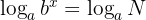
Applying property  and solving for '
and solving for ' ' we obtain:
' we obtain:
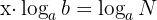

Therefore:

Example: Rewrite  in
in 
Applying: 
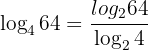
Solve an Expression with Combined Operations Applying the Properties of Logarithms
Example: Solve the operation 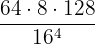 applying the properties of logarithms.
applying the properties of logarithms.
Let's equate the expression we want to solve to ' ':
':
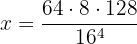
Since all numbers are powers of  , we can apply
, we can apply  on both sides:
on both sides:

Applying the properties of logarithms on the right side we obtain:
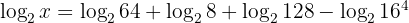
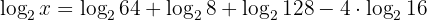
Solving the logarithms:

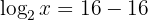
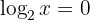
Rewriting in exponential notation:


Thus:
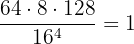
Write an Expression Containing Operations with Logarithms as an Expression Containing a Single Logarithm
Example: Write the following operation with logarithms as an expression with a single logarithm

Applying the properties of logarithms: