A logarithm is the exponent to which a number (called the base) must be raised to obtain a given number. A logarithm finds the exponent 
for a base 
that results in a specific value 
.
Example:
If the base is 
and the result is 
, what exponent must 
be raised to in order to get 
? As you can see, the exponent used to reach from base is 
.
The corresponding logarithmic notation is:
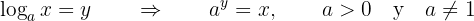
where is the base, is the result, and is the exponent. It's important to note that the base must be positive (
) and not equal to one.
From this definition, we can conclude the following:
- A logarithm with a negative base does not exist.
- The logarithm of a negative number does not exist.
- The logarithm of zero does not exist.
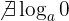
- The logarithm of 1 is zero.
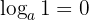
- The logarithm of a base to itself is 1.
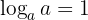
- The logarithm of a power of is equal to the exponent.
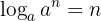
Logarithmic Properties
1Log of a product is the sum of the logs of the factors:
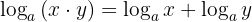
Example:
2Log of a quotient is the log of the numerator minus the log of the denominator:
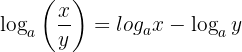
Example:
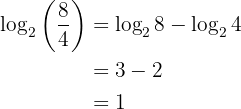
3Log of a power is the exponent multiplied by the log of the base:
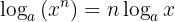
Example:
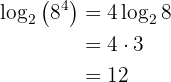
4Log of a root is the log of the radicand divided by the index:
Example:
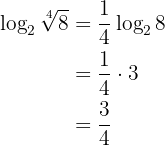
5Change of base formula:
Example:
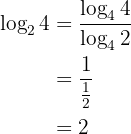
Since their invention, logarithms have become a powerful tool for handling very large numbers. Because they work with exponents, they transform complex multiplication into simple addition. Thanks to these properties, logarithms make many mathematical operations easier — making them well worth studying.
Summarize with AI:
Did you like this article? Rate it!
Loading...
