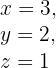A matrix is a mathematical structure that allows organizing data in rows and columns, facilitating the representation and manipulation of information in various fields, such as engineering, physics, economics and computer science. Matrix exercises help us understand how to work with them, from basic operations like addition and multiplication, to more advanced concepts like determining inverses.
Solve the following problems
Given the matrices
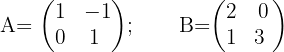
Calculate the following sums and subtractions:
a 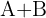
b 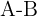
a 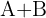
We add the elements that are in the same position of both matrices:
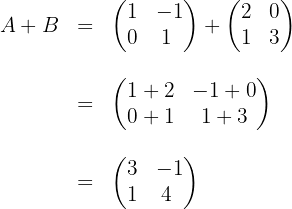
b 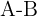
We subtract the elements that are in the same position of both matrices:
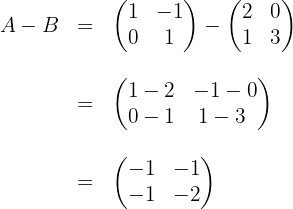
Given the matrices:
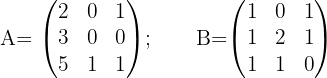
Calcular:
a 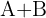
b 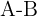
a 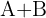
We add the elements that are in the same position of both matrices:
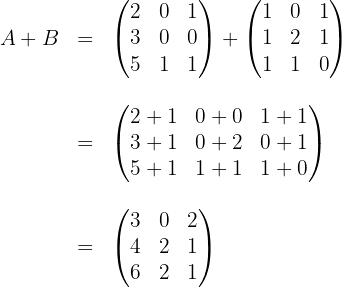
b 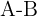
We subtract the elements that are in the same position of both matrices:

Given the matrices
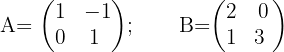
Verify if 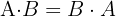 holds
holds
1 We calculate 
We multiply row  by column
by column 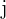 (dot product) to obtain element
(dot product) to obtain element 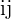
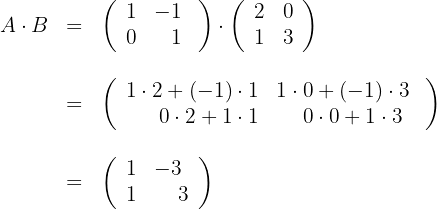
2 We calculate 
We multiply row  by column
by column 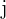 (dot product) to obtain element
(dot product) to obtain element 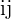
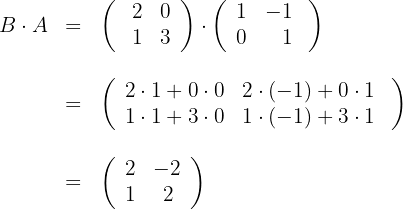
3 With the above we verify that 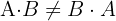
Given the matrices
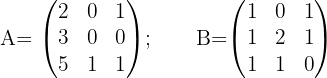
Verify if 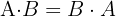 holds
holds
1 We calculate 
We multiply row  by column
by column 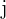 (dot product) to obtain element
(dot product) to obtain element 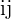

2 We calculate 
We multiply row  by column
by column 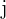 (dot product) to obtain element
(dot product) to obtain element 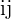

3 With the above we verify that 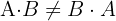
Given the matrices
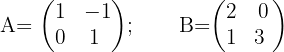
Calculate:
a 
b 
We remember that the transpose of a matrix is obtained by interchanging the rows with the columns
a We calculate 
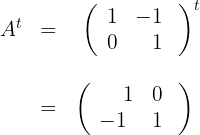
b We calculate 
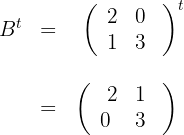
Given the matrices:
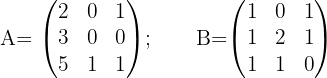
Calculate:
a
b
We remember that the transpose of a matrix is obtained by interchanging the rows with the columns
a We calculate 
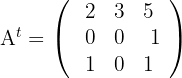
b We calculate 
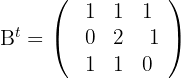
Given the matrices:
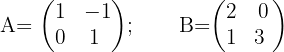
Calculate:
a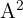
b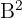
a We calculate 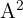
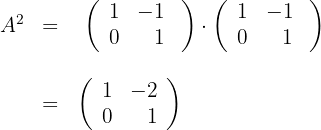
b We calculate 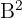
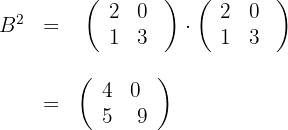
Given the matrices
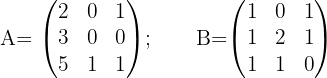
Calculate:
a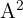
b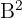
a We calculate 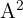

b We calculate 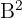

Find 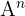 for
for
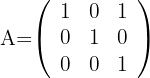
and 
1 We calculate 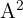

2 We calculate 
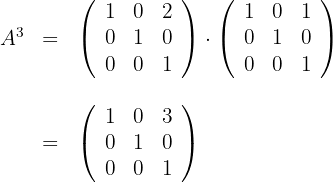
3 We notice that the element found in position  matches the power of
matches the power of  , so we propose for power
, so we propose for power 

4 Let's see if the proposed formula holds for power 
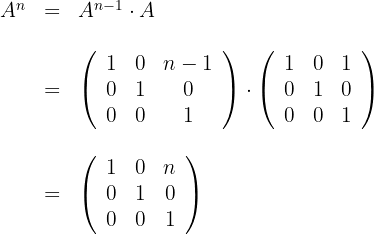
With the above we verify that the proposed formula is valid for any power 
Prove that 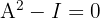 , where
, where
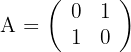
1 We calculate 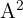
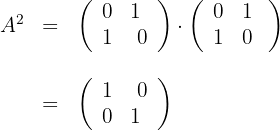
2 We substitute in the left side of the equation and calculate
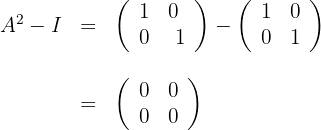
Thus, we have proved the requested equality.
Prove that 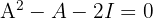 , where
, where
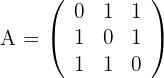
1 We calculate 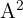

2 We substitute in the left side of the equation and calculate

Thus, we have proved the requested equality.
Calculate the inverse matrix of
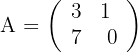
1 Construct a matrix of type 
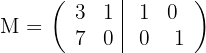
2 Use the Gauss method to transform the left half,  , into the identity matrix, and the resulting matrix on the right side will be the inverse matrix
, into the identity matrix, and the resulting matrix on the right side will be the inverse matrix 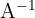 .
.
We make 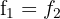
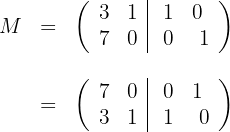
We make 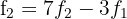
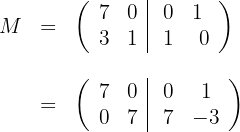
We make 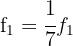 y
y 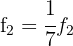
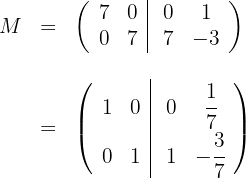
3 The inverse matrix is
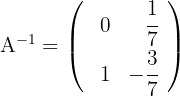
Calculate the inverse matrix of
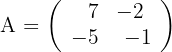
1 Construct a matrix of type 
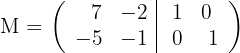
2 Use the Gauss method to transform the left half,  , into the identity matrix, and the resulting matrix on the right side will be the inverse matrix
, into the identity matrix, and the resulting matrix on the right side will be the inverse matrix 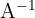 .
.
We make 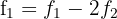
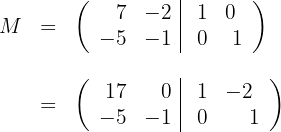
We make 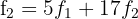
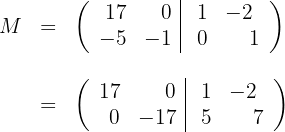
We make 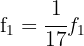 and
and 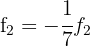
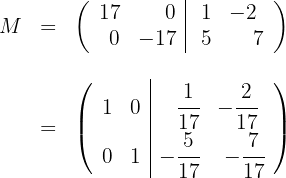
3 The inverse matrix is
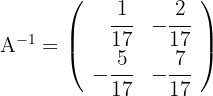
Calculate the inverse matrix of:

1 Construct a matrix of type 

2 Use the Gauss method to transform the left half,  , into the identity matrix, and the resulting matrix on the right side will be the inverse matrix
, into the identity matrix, and the resulting matrix on the right side will be the inverse matrix 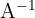 .
.
We make 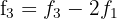

We make  and
and 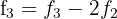
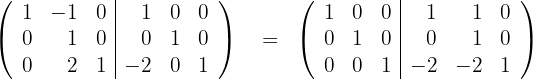
3 The inverse matrix is
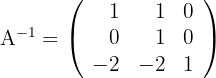
Obtain matrices  and
and  that satisfy the system:
that satisfy the system:
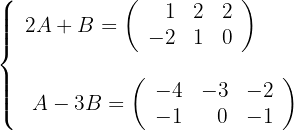
1 We multiply the second equation by 

2 We add member by member and solve for 

3 If we multiply the first equation by 3 and add member by member we obtain:
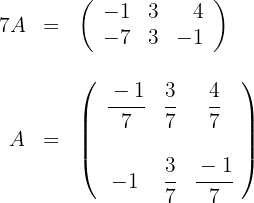
A factory produces two washing machine models,  and
and  , in three finishes:
, in three finishes:  and
and  . It produces model
. It produces model 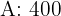 units in finish
units in finish  ,
,  units in finish
units in finish  and
and  units in finish
units in finish  . It produces model
. It produces model 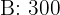 units in finish
units in finish  ,
,  units in finish
units in finish  and
and  units in finish
units in finish  . Finish
. Finish  takes
takes  workshop hours and
workshop hours and  administration hour. Finish
administration hour. Finish  takes
takes  workshop hours and
workshop hours and  administration hours. Finish
administration hours. Finish  takes
takes  workshop hours and
workshop hours and 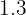 administration hours.
administration hours.
1 Represent the information in two matrices.
2 Find a matrix that expresses the workshop and administration hours used for each of the models.
Production matrix:
Rows: Models  ; Columns: Finishes
; Columns: Finishes 
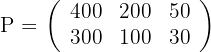
Cost matrix in hours:
Rows: Finishes  ; Columns: Cost in hours:
; Columns: Cost in hours: 
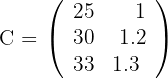
Matrix that expresses the workshop and administration hours for each of the models:

Calculate the rank of the following matrix:

We perform elementary row operations:
1 We make 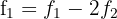
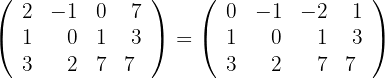
2 We make 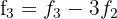
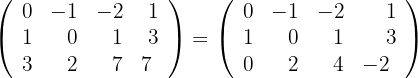
3 We make 

Thus 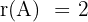 .
.
Given:
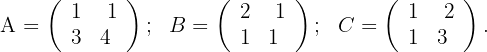
Calculate the value of  in the following equations:
in the following equations:
1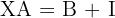
2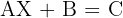
3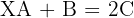
4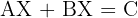
5
We solve for variable  in each of the equations
in each of the equations
1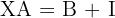
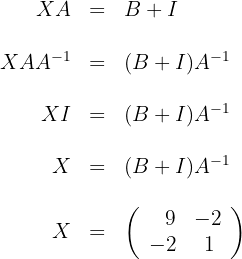
2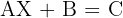

3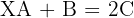
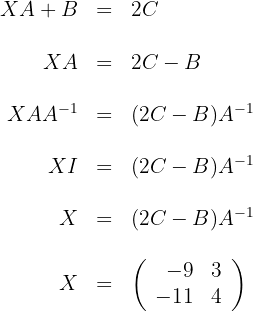
4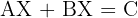

5

Solve in matrix form the system:
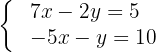
1 We write in matrix form
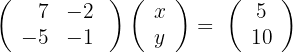
2 We solve the equation
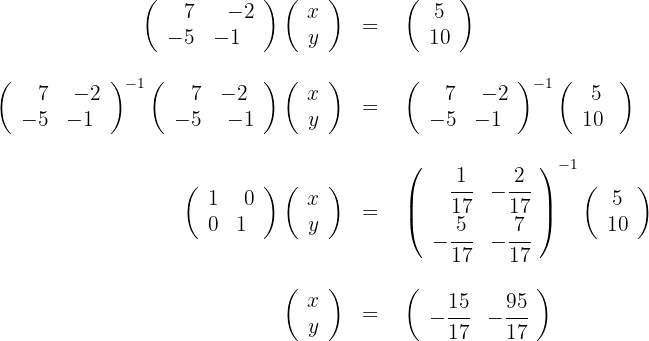
3 Thus, the solution is
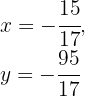
Solve in matrix form the system:
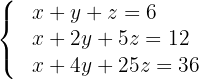
1 We write in matrix form
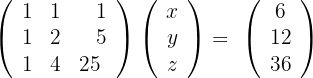
2 We solve the equation
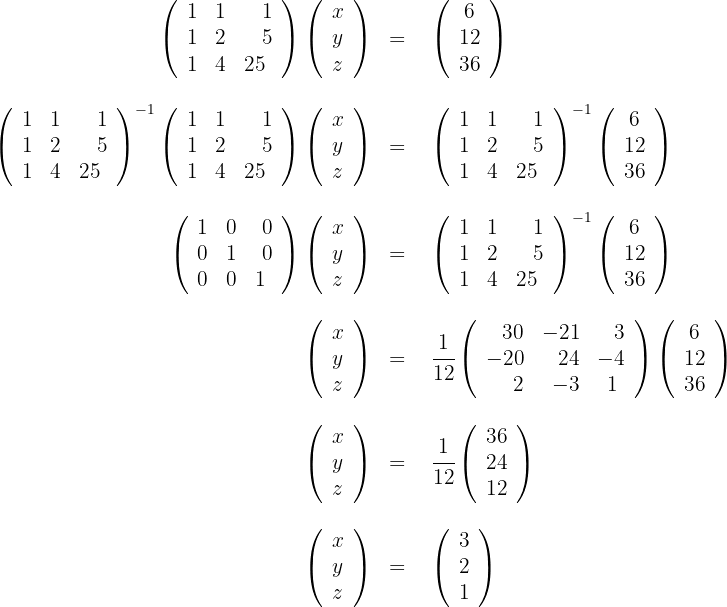
3 Thus, the solution is