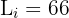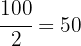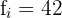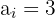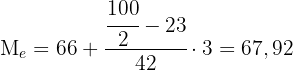Chapters
What Is the Median?
The median is the value that occupies the central position of all data when they are ordered from smallest to largest.
The median is represented by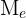 
The median can only be found for quantitative variables.
Simple Median Calculation Example
1 We order the data from smallest to largest.
2 If the series has an odd number of measurements, the median is the central score.
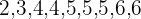
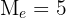
3 If the series has an even number of scores, the median is the average between the two central scores.
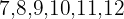
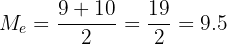
Formula and Calculation of the Median for Grouped Data
The median is found in the interval where the cumulative frequency reaches half of the sum of the absolute frequencies.
That is, we have to find the interval in which it is located.
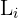is the lower limit of the class where the median is found
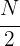is the semi-sum of the absolute frequencies
is the absolute frequency of the median class
is the cumulative frequency before the median class
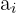is the class width
The median is independent of the interval widths.
Example of Median Calculation for Statistical Distribution
Calculate the median of a statistical distribution given by the following table:
| |
|---|---|
 |  |
 |  |
 |  |
 |  |
 |  |
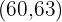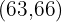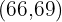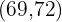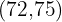First, we will create a new column with the cumulative frequency values:
In the first cell we place the first absolute frequency. In the second cell we add the value of the previous cumulative frequency plus the corresponding absolute frequency and so on until the last one, which must equal 
|  | |
|---|---|---|
| | |
| |  |
| |  |
| |  |
| |  |
|
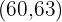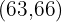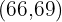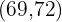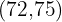We look for the interval where the median is located, for this we divide 
by 
because the median is the central value
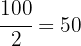
We look in the cumulative frequency column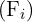 
for the interval that contains 
Median class: 
We will apply the formula for calculating the median for grouped data, extracting the following data:
Did you like this article? Rate it!
Loading...
