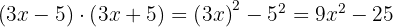Chapters
In this article, we explain the most common notable products, along with practical examples to deepen your understanding of the theory.
What are notable products?
Notable products are simply special multiplication patterns between algebraic expressions that stand out due to their frequent use in mathematics. The term “product” refers to multiplication, while “notable” refers to their importance or repeated appearance.
Once you’ve learned these patterns, there’s no need to multiply expressions step-by-step — just apply the known rules for each type of notable product.

Square of a Binomial
The square of a binomial equals:
- Plus the square of the second term.
- The square of the first term,
- Plus double the product of both terms,
If both signs are the same, the middle term is positive:
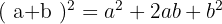
If the signs are different, the middle term is negative:
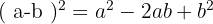
Examples of exercises with binomials squared:
1 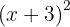
To solve this case, we use the first formula with  and
and  . We substitute and get:
. We substitute and get:
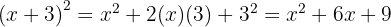
2 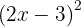
To solve this case, we use the second formula with 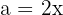 and
and  . We substitute and get:
. We substitute and get:

3 
To solve this case, we use the first formula with 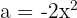 and
and  . We substitute and get:
. We substitute and get:
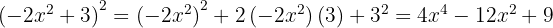
4 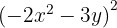
To solve this case, we use the first formula with 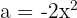 and
and 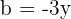 . We substitute and get:
. We substitute and get:
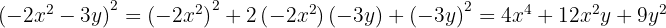
💡 Review notable identities with a private math tutor.
Sum and Difference
The product of a sum and a difference equals the difference of squares:

Examples of exercises with sum and difference:
1 
Using the formula, we set 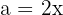 and
and 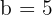 , then substitute:
, then substitute:

2 
Using the formula, we set 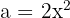 and
and 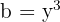 , then substitute:
, then substitute:

Cube of a Binomial
A binomial cubed is equal to:
The cube of the first term, plus three times the square of the first term times the second, plus three times the first term times the square of the second, plus the cube of the second term.
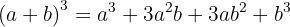
We recommend memorizing this formula.
Examples of Exercises with Binomials Cubed:
1 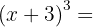
Using the formula, we set  and
and  , then substitute:
, then substitute:
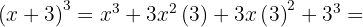
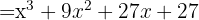
2 
Using the formula, we set 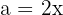 and
and  , then substitute:
, then substitute:

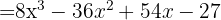
If we look at the signs, they are: +, −, +, −. This gives us a variation of the previous formula:
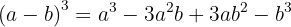
3 
Using the formula 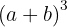 , we set
, we set 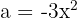 and
and 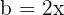 , then substitute:
, then substitute:
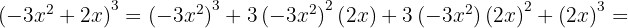
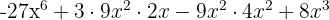
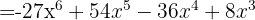
The resulting signs are: −, +, −, +. Another variation we can use is:
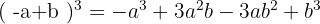
4 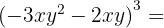
Using the formula 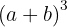 , we set
, we set 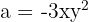 and
and 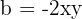 , then substitute:
, then substitute:


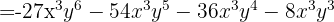
The signs are: −, −, −, −. We can use this variation:
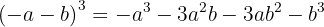
Square of a Trinomial
A trinomial squared is equal to:
The square of the first term, plus the square of the second, plus the square of the third, plus double the product of the first and second, plus double the product of the first and third, plus double the product of the second and third.

Examples of Exercises with Trinomials Squared:
1 
To solve this exercise, we set 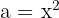 ,
, 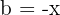 , and
, and  , then substitute into the formula:
, then substitute into the formula:
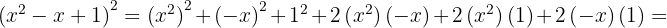
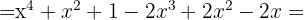

2 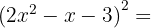
To solve this exercise, we set 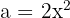 ,
, 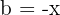 , and
, and 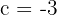 , then substitute into the formula:
, then substitute into the formula:

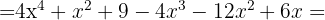
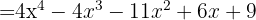
📌 Are you looking for a math tutor? Find one on Superprof!
Sum of Cubes
Now, instead of expanding the expressions, we'll factor them — that is, we’ll rewrite them as the product of two other expressions.
The way to factor the sum of cubes is:
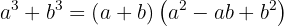
Example of an Exercise with Sum of Cubes:
Factor the following expression:
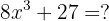
First, we look at how we can rewrite the terms to use the cube factoring formula. In this case, we can rewrite the expression as:
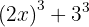
Using the cube formula and setting 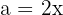 and
and  , we get:
, we get:
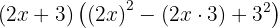
Expanding, we have:
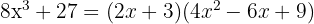
Difference of Cubes
The formula for factoring the difference of cubes is:
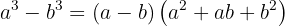
Example of an Exercise with Difference of Cubes:
Factor the following expression:

As before, the first step is to rewrite the terms so we can use the cube factoring formula. In this case, we rewrite the expression as:
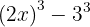
Using the cube formula and setting 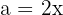 and
and  , we get:
, we get:
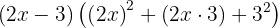
Expanding, we have:
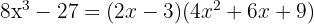
Product of Two Binomials with a Common Term
When you multiply two binomials that share a common term, the result simplifies nicely:
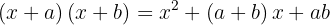
Example of an Exercise with Binomials That Share a Common Term:
Expand the following expression:
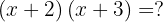
There’s no need to memorize the formula — by following the multiplication steps and paying close attention to signs, we simply calculate step by step:
First, multiply the terms from the first parenthesis with those in the second:
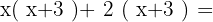
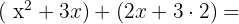
We recommend keeping the parentheses until the end — that way, you won’t forget to change a + to a − (or vice versa) if needed. In this case, no sign changes are necessary.
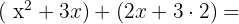
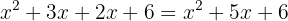
Solved Examples of Notable Products
Expand the binomials squared:
1 
We use the formula 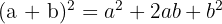 , where
, where  and
and 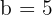 , substitute, and we get:
, substitute, and we get:

2 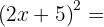
We use the formula 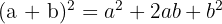 , where
, where 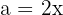 and
and 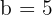 , substitute, and we get:
, substitute, and we get:
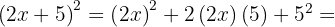
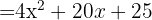
3 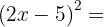
We use the formula 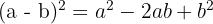 , where
, where 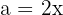 and
and 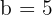 , substitute, and we get:
, substitute, and we get:
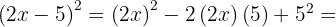
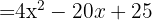
4 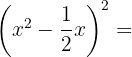
We use the formula 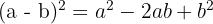 , where
, where 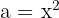 and
and 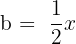 , substitute, and we get:
, substitute, and we get:
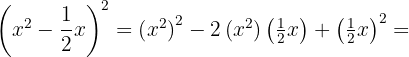
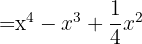
Expand the binomials cubed:
1 
We use the formula  , where
, where 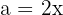 and
and  , substitute, and we get:
, substitute, and we get:
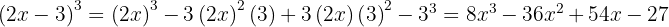
2 
We use the formula 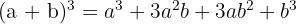 , where
, where  and
and  , substitute, and we get:
, substitute, and we get:
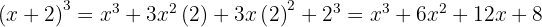
3 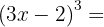
We use the formula  , where
, where 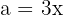 and
and  , substitute, and we get:
, substitute, and we get:
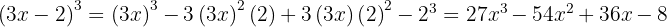
4 
We use the formula 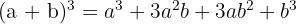 , where
, where 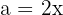 and
and 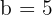 , substitute, and we get:
, substitute, and we get:
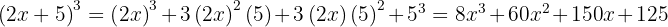
Expand the sum and difference products:
1 
We use the formula 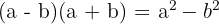 , where
, where 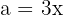 and
and  , substitute, and we get:
, substitute, and we get:
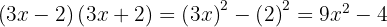
2 
We use the formula 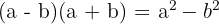 , where
, where  and
and 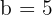 , substitute, and we get:
, substitute, and we get:

3 
We use the formula 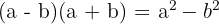 , where
, where 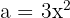 and
and  , substitute, and we get:
, substitute, and we get:

4 
We use the formula 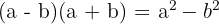 , where
, where 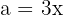 and
and 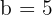 , substitute, and we get:
, substitute, and we get: