
Understanding Percentages
A percentage indicates a rate per 100 units, so 7% of some quantity means that out of every 100 units only 7 are taken. In the following exercises, this is expressed as:
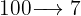
To make our work easier, the first thing we should do is identify the element we are going to calculate. This can be some quantity or some percentage. The element we calculate will be substituted by the variable x in the table shown below:
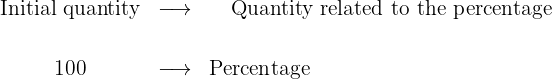
To calculate the value, we only need to make a proportionality, in the same order that we have previously arranged the data:

That is:
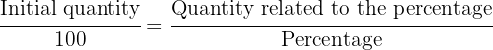
When replacing any of the values with x, we just need to solve for x. For example, suppose we want to calculate the percentage, then we substitute "percentage" with x:
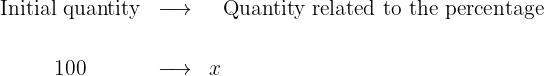
Our relationship would be of the form:
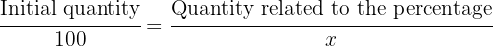
And when solving it we would obtain:
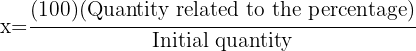
Similarly, if we write the data in another order:
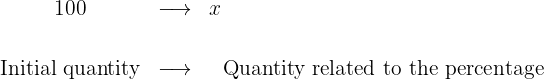
We can use our relationship in the following way:
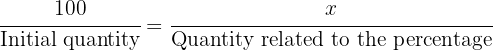
And when solved, it remains the same as the previous one.
Real-life Problems Using Percentages
Out of 800 students in a school, 600 have gone on a trip. What percentage of students went on the trip?
1 We identify and organize the data, substituting the data to calculate with x:
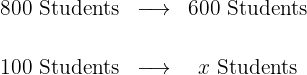
2 We establish the relationship of the data, solve for x and calculate:


When purchasing a vehicle whose price is $8800, we get a 7.5% discount. How much do we have to pay for the vehicle?
1 We identify and organize the data, substituting the data to calculate with x:
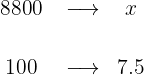
2 We establish the relationship of the data, solve for x and calculate:


3 We subtract the value of 'x' from the original cost
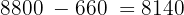
4 It can also be calculated directly as follows:
There is a 7.5% discount, meaning we are only paying 92.5% of the total, so instead of taking 7.5 out of every 100, we only need to calculate 92.5% or 92.5 out of every 100:
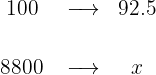
5 We establish the relationship of the data, solve for x and calculate:
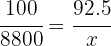
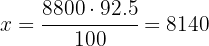
The price of a computer is $1200 without tax. How much do we have to pay for it if the tax is 16%?
1 Due to tax there is a 16% surcharge, meaning for every $100 we pay $16 more, therefore instead of $100 we pay $116
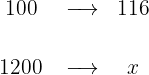
2 We establish the relationship of the data, solve for x and calculate:


When buying a monitor that costs $450 we get an 8% discount. How much do we have to pay?
1 There is an 8% discount, meaning for every $100 we pay $8 less, therefore instead of $100 we pay $92
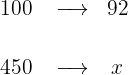
2 We establish the relationship of the data, solve for x and calculate:

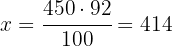
An item is sold with a 15% profit over the cost price. If it was purchased for $80, find the selling price.
1 We identify and organize the data, substituting the data to calculate with x:
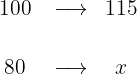
2 We establish the relationship of the data, solve for x and calculate:


What price should we mark on an item whose purchase was $180 to gain 10% when selling it?
1 Purchase price is $180 and we intend to gain 10%
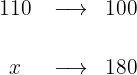
2 We establish the relationship of the data, solve for x and calculate:

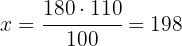
We want to sell some shoes through a second-hand clothing app. We bought the shoes for $280 and now want to sell them 12% cheaper. What price should we mark on the app?
1 We have
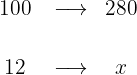
2 We establish the relationship of the data, solve for x and calculate:

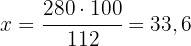
3 Now we have 12% of 280, we need to know what price we will put on the app. For this, we subtract:

To sell the shoes 12% cheaper, we will sell them on the app for 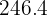
An object is sold losing 20% on the purchase price. Find the selling price of said item whose purchase value was $150.
1 If the purchase price is $100 and 20% is lost, the selling price will be $80
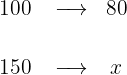
2 We establish the relationship of the data, solve for x and calculate:

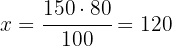
A dealership has 120 cars, 35% of them are white and 5% red. How many cars of each color are there?
We need to calculate 35% and 5% of 120. Since the total number of cars is 120, we identify it with 100%.
1 We first calculate the number of white cars

That is,
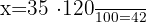
2 Now let's see the number of red cars
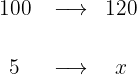
Therefore, the number of red cars is

Out of 684 shots Daniel took, he missed 513. What percentage of missed shots does Daniel have?
1 We identify 684 with 100% and want to see what percentage 513 represents
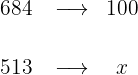
2 We establish the relationship of the data, solve for x and calculate:
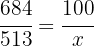
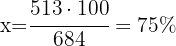
18% of the trees in the main square garden are almond trees and the rest are orange trees. If there are 45 almond trees in the square, how many trees are there in total in the square?
1 We only need to identify 18% with 45 to calculate 100%:
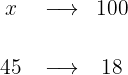
2 We establish the relationship of the data, solve for x and calculate:
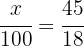
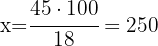
That is, there are a total of 250 trees.
In a store they want to reduce the price of a $25 book by $5. What percentage discount would they be applying?
1 Since $25 is 100%,
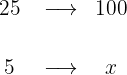
2 We establish the relationship of the data, solve for x and calculate:
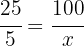
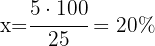
That is, if they reduce $5, they would be applying a 20% discount from the initial price.
Adrian was 165cm (5 feet 5 inches) tall, but in one year he has grown 8%. How tall is Adrian now? How many centimeters has he grown?
1 The 165cm (5 feet 5 inches) is 100% of Adrian's height. By growing 8%, his height is now 108% of 165cm (5 feet 5 inches):
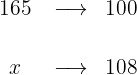
2 We establish the relationship of the data, solve for x and calculate:
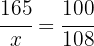
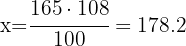
Adrian is 178.2cm (5 feet 10.2 inches) tall, meaning he grew 13.2cm (5.2 inches).
Lara got 85% of the English test questions right. If the test had a total of 160 questions, how many questions did she get wrong?
1 We identify 160 with 100%. Since she got 85% right, she got 15% wrong. Therefore, we will calculate 15% of 160:

2 We establish the relationship of the data, solve for x and calculate:

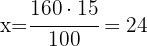
Therefore, Lara got 24 questions wrong.
In a classroom of 80 students, 45% are girls, of which 25% are blonde. How many blonde girls are there in the classroom?
1 To calculate the number of blonde girls we need to calculate the total number of girls in the classroom, in this case we identify the 80 students as 100%
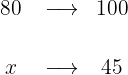
Therefore
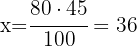
2 Now, let's calculate the total blonde girls out of the 36, in this case 100% is the total number of girls
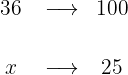
Then
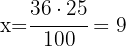
There are 9 blonde girls in the classroom.
Mastering percentage calculations opens doors to better financial literacy and problem-solving abilities in everyday situations. Whether you're working through these exercises independently or seeking extra help, Superprof offers access to experienced math teachers who can provide tailored instruction to strengthen your understanding of percentages and related mathematical concepts, both in-person and online. Find your teacher today!












