
Definition of Permutations
A permutation is the number of different ways in which the elements of a set can be arranged. If the set consists of  elements and these are to be arranged in groups of size
elements and these are to be arranged in groups of size  , then it is required that
, then it is required that 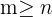 .
.
The following must be taken into account:
1 The order of the groups does matter, since the exchange between two different elements generates a new permutation.
2 Elements are not repeated, since if they are repeated or are equal to each other, exchanging them does not generate a new permutation.
To obtain the total number of ways in which  elements can be placed in
elements can be placed in  positions, the following formula is used:
positions, the following formula is used:

If in a given case, 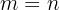 to calculate the total permutations the following formula is used:
to calculate the total permutations the following formula is used:
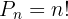
Below, analyze the following examples using what was previously mentioned.
Examples of Permutation Problems
1 Calculate the permutations of  elements in
elements in  positions.
positions.
Solution:
In this case 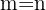 so we use
so we use
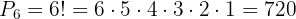
Thus, there are  different ways to arrange
different ways to arrange  elements.
elements.
2 How many numbers with 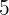 different digits can be formed with the digits:
different digits can be formed with the digits: 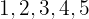 ?
?
Solution:
Since we have  different digits, and we want five-digit numbers, then
different digits, and we want five-digit numbers, then  so we use
so we use
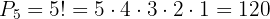
Thus, there are  different five-digit numbers formed with the digits
different five-digit numbers formed with the digits  .
.
3 In how many different ways can eight people sit in a row of eight seats?
Solution:
Since we have  people and they are different, plus we are not told that there are two identical ones and they want to sit in eight seats, then
people and they are different, plus we are not told that there are two identical ones and they want to sit in eight seats, then 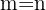 so we use
so we use
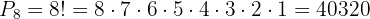
Thus, there are 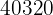 different ways to seat eight people in eight seats.
different ways to seat eight people in eight seats.
4 In how many different ways can eight people sit in a row of seven seats?
Solution:
Since we have  people and they are different, plus we are not told that there are two identical ones and they want to sit in
people and they are different, plus we are not told that there are two identical ones and they want to sit in  seats, then
seats, then  so we use
so we use
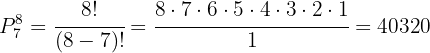
Thus, there are 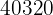 different ways to seat eight people in seven seats. This is because there is always one person left standing.
different ways to seat eight people in seven seats. This is because there is always one person left standing.
5 In how many different ways can eight people sit in a row of five seats?
Solution:
Since we have  people and they are different, plus we are not told that there are two identical ones and they want to sit in
people and they are different, plus we are not told that there are two identical ones and they want to sit in  seats, then
seats, then  so we use
so we use
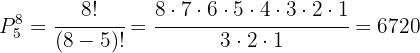
Thus, there are 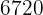 different ways to seat eight people in five seats.
different ways to seat eight people in five seats.
6 How many different ways are there to place the letters  in three positions?
in three positions?
Solution:
In this case 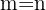 so we use
so we use
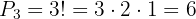
Thus, there are  different ways to arrange the letters
different ways to arrange the letters 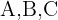 and these are:
and these are:

7 If we have 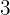 elements and we want to place them in
elements and we want to place them in 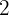 positions, in how many ways can this be done?
positions, in how many ways can this be done?
Solution:
In this case  so we use
so we use
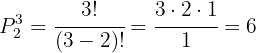
Thus, there are  different ways to arrange three elements in two positions. If we denote the elements with the letters
different ways to arrange three elements in two positions. If we denote the elements with the letters 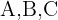 the different ways to arrange them in two positions are:
the different ways to arrange them in two positions are:
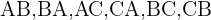
8 If we have 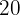 students and we want to form a committee of
students and we want to form a committee of 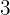 students, how many different committees can we form?
students, how many different committees can we form?
Solution:
In this case  so we use
so we use
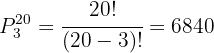
Thus, there are 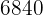 different ways to arrange twenty students in committees of size three.
different ways to arrange twenty students in committees of size three.
There are many applications of permutations because there are very complex counts that are simplified in this way. It must be emphasized that in permutations the order in which the elements are presented does matter.
And you, where do you apply permutations in your daily life?












