Chapters

Addition of Polynomials
To add two or more polynomials, you must add the coefficients of terms whose literal parts are equal, that is, the variables and exponents (or degrees) must be the same in the terms to be added.
Method 1 for Adding Polynomials
Steps:
1 Add the like terms.
2 Order the polynomials from the highest degree term to the lowest.
3 Group the monomials of the same degree.
Example of the first method for adding polynomials
Add the polynomials
1 We order the polynomials, if they are not already ordered.


2 We group the monomials of the same degree.

3 We add the like terms.

Method 2 for Adding Polynomials
We can also add polynomials by writing one below the other, so that like terms are in columns and can be added.
Example of the second method for adding polynomials
Add the polynomials

1 Arrange the terms in columns from highest to lowest degree, and add.

Thus,
2 
Subtraction of Polynomials
Polynomial subtraction consists of adding the opposite of the subtrahend to the minuend.
Example of polynomial subtraction
Subtract the polynomials

1 We obtain the opposite of the subtrahend  .
.

2 We group.

3 Result of the subtraction.

Multiplication of Polynomials
1. Multiplication of a Number by a Polynomial
The multiplication of a number by a polynomial is another polynomial. The resulting polynomial has the same degree as the initial polynomial. The coefficients of the resulting polynomial are the product of the coefficients of the initial polynomial by the number, keeping the same literal parts.
Examples:
1 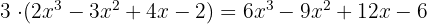
2 
2. Multiplication of a Monomial by a Polynomial
In multiplying a monomial by a polynomial, the monomial is multiplied by each and every one of the monomials that form the polynomial.
Remember that we must first multiply signs, then multiply the corresponding monomials, for which we must multiply the coefficients, and then perform the multiplication of the literal part, where, when multiplying equal variables, the exponents are added.
Example:

3. Multiplication of Polynomials
This type of operation can be carried out in two different ways.
Method 1 for Multiplying Polynomials
Steps:
- Each monomial of the first polynomial is multiplied by all elements of the second polynomial.
- The monomials of the same degree are added, obtaining another polynomial whose degree is the sum of the degrees of the polynomials being multiplied.
Example:
Multiply the following polynomials

1 Each monomial of the first polynomial is multiplied by all elements of the second polynomial.
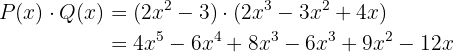
2 The monomials of the same degree are added.

3 Another polynomial is obtained whose degree is the sum of the degrees of the polynomials being multiplied.
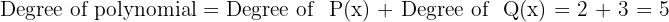
and 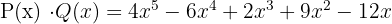
Method 2 for Multiplying Polynomials
We can also multiply polynomials by writing one polynomial below the other. In each row, each of the monomials of the second polynomial is multiplied by all the monomials of the first polynomial. Like terms are placed in the same column and then like terms are added.
Example:
Multiply the following polynomials
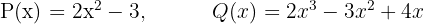
Since polynomial multiplication follows the commutative property, we have taken the simpler polynomial as the multiplier polynomial.
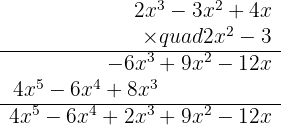
Division of Polynomials
We will approach the explanation with an example.
Example:
Solve the division of polynomials
P(x) : Q(x)
1 On the left we place the dividend. If the polynomial is not complete, we leave gaps in the corresponding places.

2 On the right we place the divisor inside a box.
3 We divide the first monomial of the dividend by the first monomial of the divisor.
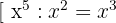
4 We multiply each term of the divisor polynomial by the previous result and subtract it from the dividend polynomial:
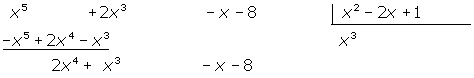
5 We divide the first monomial of the dividend by the first monomial of the divisor again. And we multiply the result by the divisor and subtract it from the dividend.
obtaining
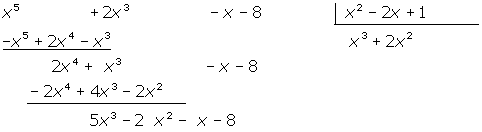
6 We proceed as before. And this time
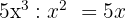
thus
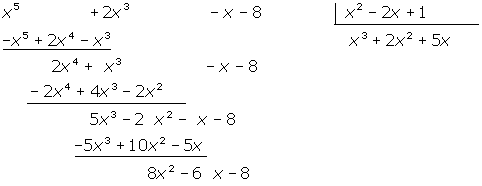
7 As in the previous steps, we divide  by
by  , and get
, and get  .
.
We multiply each term of the divisor by  and get:
and get:
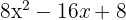
We proceed with the subtraction:
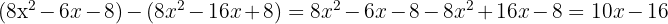
We conclude that 10x − 16 is the remainder, because its degree is less than that of the divisor and therefore division cannot continue. And the quotient is 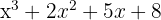
Remember that, whether you're looking for an online or in-person math teacher, you can find them on Superprof.












