Chapters
To raise a fraction to a power, apply the exponent to both the numerator and denominator.

provided that 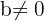
Example: Evaluate the power 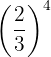


Powers of Fractions with Negative Exponents
A power of a fraction with a negative exponent is equal to another power whose base is the reciprocal of the original fraction with a positive exponent.
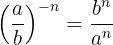
Example: Evaluate the power 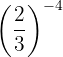
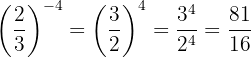
Properties of Powers of Fractions
1. Any fraction raised to the power of zero equals one.
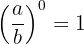
2. Any fraction raised to the power of one equals the same fraction.
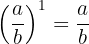
3. The product of powers with the same base is another power with the same base whose exponent equals the sum of the exponents.

4. The division of powers with the same base is another power with the same base whose exponent equals the difference of the exponents.
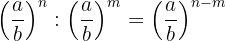
5. The power of a power is another power with the same base whose exponent equals the product of the exponents.

6. The product of powers with the same exponent is another power with the same exponent whose base equals the product of the bases.
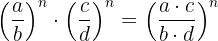
7. The quotient of powers with the same exponent is another power with the same exponent whose base equals the quotient of the bases.

Practice Exercises
Simplify the following operations with powers:
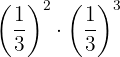
The powers have the same base, so by property 3 the base is the same and the exponents are added.
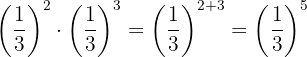

The powers have the same base, so by property 3 the base is the same and the exponents are added.
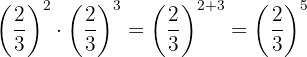

The powers have the same base, so by property 3 the base is the same and the exponents are added.

By property 2, any fraction raised to the power of one equals the same fraction.

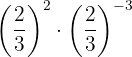
The powers have the same base, so by property 3 the base is the same and the exponents are added.
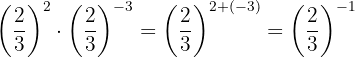
To remove the negative sign from the exponent, we must write the reciprocal fraction and then apply property 2, which tells us that any fraction raised to the power of one equals the same fraction.
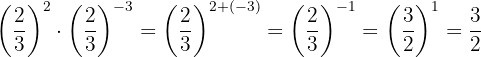

The powers have the same base, so by property 3 the base is the same and the exponents are added.
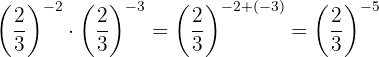
To remove the negative sign from the exponent, we must write the reciprocal fraction.
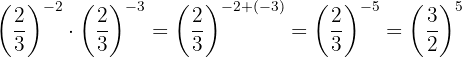
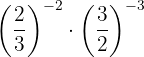
Since the powers do not have the same base, we take the reciprocal fraction of the second power to obtain a positive exponent.

By property 2, any fraction raised to the power of one equals the same fraction.
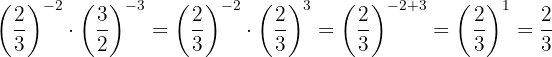
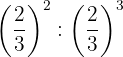
The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
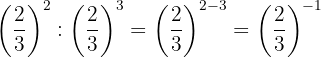
To remove the negative sign from the exponent, we must write the reciprocal fraction; then by property 2, any fraction raised to the power of one equals the same fraction.
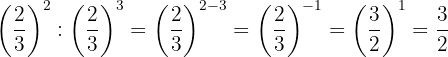

The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
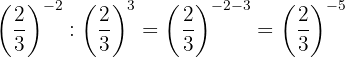
To remove the negative sign from the exponent, we must write the reciprocal fraction.
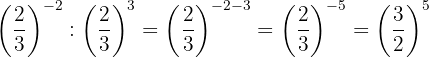
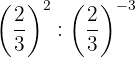
The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
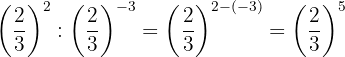
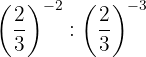
The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
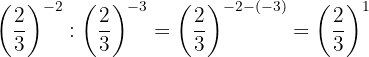
By property 2, any fraction raised to the power of one equals the same fraction.
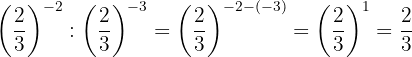

We take the reciprocal fraction of the first power to change the sign of the exponent.

The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
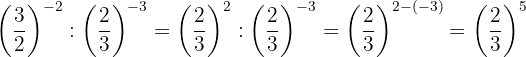

The powers have the same base, so by property 4 the base is the same and the exponents are subtracted.
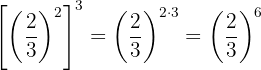
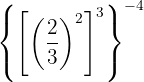
This is a power of a power, so by property 5 the base is the same and the exponents are multiplied.
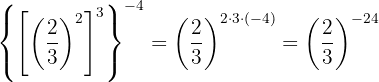
To remove the negative sign from the exponent, we must write the reciprocal fraction.
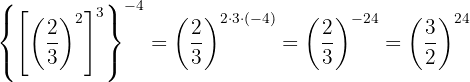
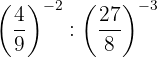
We decompose the numbers into factors and apply property 5 for power of a power.

We take the reciprocal fraction of the first power to change the sign of the exponent and apply property 4 for quotient of powers.

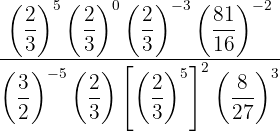
We will try to express all fractions with the same numerator and denominator; to do this, we decompose into factors the numbers that are not prime.

There are elements that are powers of powers, so we apply property 5 to write them as a single power.

For the powers with base  and negative exponents, we write the reciprocal fraction with a positive exponent.
and negative exponents, we write the reciprocal fraction with a positive exponent.

Both in the numerator and in the denominator, we multiply the powers with the same base using property 3 and divide the results using property 4. Finally, we write the reciprocal fraction with a positive exponent.

Summarize with AI:












