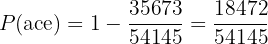Here are some probability problems for you to practice solving:
Find the probability that when throwing two coins in the air, the following results occur:
A Two heads
B Two tails
C One head and one tail
A Two heads.
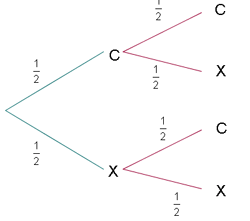
We multiply the probability of getting a head on one coin (1/2), by the probability of the same event on the other coin (1/2), because they are independent events
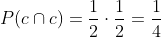
B Two tails.
The event of getting a tail on one coin and also tail on the other, are independent events and each has a probability of (1/2) as we observe in the diagram. Because of this, both probabilities are multiplied
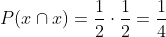
C One head and one tail.
The probability of getting one head and one tail refers to the following two possibilities: head and tail, or tail and head. This means we must first get the probability of each option (1/2)(1/2) and then add them to get the result, observe:
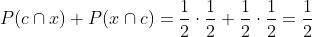
Calculate the probability of getting exactly two tails when throwing a coin three times.
The possible results per throw are head (H) or tail (T).
First we can find the ways in which two tails (T) can occur in three throws. Of three possible results n=3, let's see in how many ways r=2 of them are equal, that is, let's calculate the total number of groups of two elements (equal results) that can be extracted from a total of three elements (possible results).
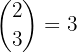
As we see there are 3. To be clearer, here we show the 3 ways
TTH, THT, HTT
Now, the total number of ways the coins can land when thrown three times, thinking that there are two options for each one is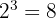
Therefore, the probability of getting exactly two tails when throwing a coin three times is
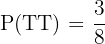
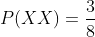
Find the probability that when picking up domino tiles, a number of points greater than 9 or that is a multiple of 4 is obtained.
In set A we put the tiles where the total points of each one is greater than nine, and in B the tiles where the number of points of each one is a multiple of four:
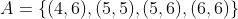
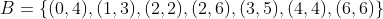
In this case we observe that tile (6,6) belongs to both sets, or in other words, 
This means we must now use the formula 
Now, taking into account that there are 28 domino tiles, the values are as follows:
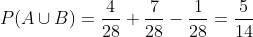
A die is loaded, so that the probabilities of obtaining the different faces are proportional to the numbers on these faces. Find:
A The probability of obtaining 6 in one throw
B The probability of getting an odd number in one throw
A The probability of obtaining 6 in one throw
Since the die is loaded, the probability of each face is proportional to the number on the corresponding face.
For example 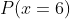
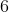
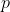
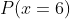
If on the other hand we sum the probabilities of each face we have the following:
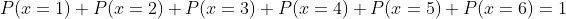
Thus:
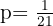
Now, the probability of obtaining a 6 is:
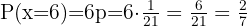
B The probability of getting an odd number in one throw
In this case it's only necessary to add the probabilities of getting all possible odd numbers.
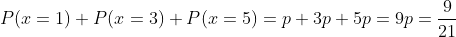
Two dice are thrown and the sum of the points obtained is recorded. Find:
A The probability that 7 comes up
B The probability that the number obtained is even
C The probability that the number obtained is a multiple of three
A The probability that 7 comes up
We group all the possibilities where the sum is seven
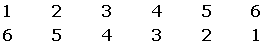
We realize there are 6 possible ways, and since there are 36 different possible ways two dice can land, then:
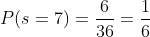
B The probability that the number obtained is even
The pairs for the number obtained to be even are
(1,1)
(1,3), (2,2),(3,1)
(1,5),(2,4),(3,3),(4,2),(5,1)
(2,6),(3,5),(4,4),(5,3),(6,2)
(4,6),(5,5),(6,4)
(6,6)
Which are 18, meaning the probability that the result obtained is even is:
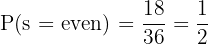
C The probability that the number obtained is a multiple of three
We realize that each of these pairs sum to some multiple of three
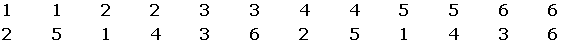
And there are 12 of them, then:
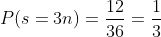
Where the result represents multiples of 3.
Three dice are thrown. Find the probability that:
A Six comes up on all
B The points obtained sum to 7
A six comes up on all
There is only one way for six to come up on all (6,6,6), and if we consider that there are 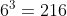
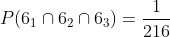
B The points obtained sum to 7
Here are the ways the dice can fall where the sum of the points is seven:

and with this list, we realize that there are 15 different ways for the sum to be 7, so the desired probability is:
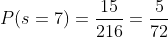
Find the probability that when throwing a die in the air, the following comes up:
A An even number
B A multiple of three
C Greater than four
A An even number
For it to be even, we have the following options: 2,4,6. This means there are 3 ways out of 6 possible, so the probability is
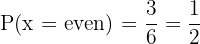
B A multiple of three
In this case the multiples of three are: 3 and 6. Therefore there are 2 ways for it to be a multiple of 3, and 6 ways a dice can fall
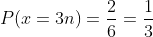
C Greater than four
In this case those greater than four are 5 and 6, leading us to the probability
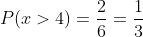
Two balls are drawn from a basket containing one white ball, one red, one green and one black. Describe the sample space when:
A The first ball is returned to the basket before drawing the second
B The first ball is not returned
A The first ball is returned to the basket before drawing the second
The first ball can be any of the four W,R,G,B and when recording which one came out and returning it to the basket, any of the four can come out again, meaning that for example if W came out first, then with the second extraction we can have WW, WR, WG or WB, and so on with the other options, leaving our sample space as
S = {WW, WR, WG, WB, RW, RR, RG, RB, GW, GR, GG, GB, BW, BR, BG, BB}
B The first ball is not returned
Since the ball drawn first is not returned, then in the second extraction one of the remaining three must come out, meaning it's no longer possible for the ball to repeat, leaving the sample space as
S = {WR, WG, WB, RW, RG, RB, GW, GR, GB, BW, BR, BG}
A basket has eight red balls, 5 yellow and seven green. One is extracted at random. Find the probability that:
A It is red
B It is green
C It is yellow
D It is not red
E It is not yellow
A It is red
Out of 20 balls total, there are 8 red ones. So the probability is
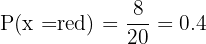
It is green
Since there are 7 green balls the probability is
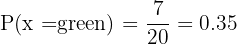
C It is yellow
Out of the 20 balls, there are 5 yellow ones, so
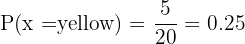
D It is not red
Since we must calculate the probability that it is NOT red, we can subtract from the total (1), the probability that it IS red, leaving the desired probability as
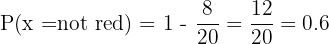
E It is not yellow
Here we use the same reasoning as in the previous section
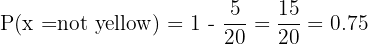
A basket contains three red balls and seven white balls. Two balls are extracted at random. Write the sample space and find the probability of:
A Extracting the two balls with replacement
B Without replacement
A Extracting the two balls with replacement
First let's describe the sample space. Since there are two types of balls, red (R) or white (W), in our first extraction we can get either of the two balls, and since the quantity of each is greater than one, then (with or without replacement), in the second extraction we can also obtain either of the two, leaving the sample space as follows
S = {RR, RW, WR, WW}
Now, when extracting a ball and then returning it to the urn (replacing it), the conditions of the first and second extraction are exactly the same, meaning they are independent events. Here we can apply the following formula that works for independent events
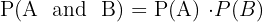
First extraction R, second R
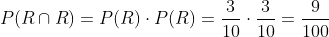
First extraction R, second W
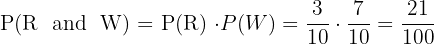
First extraction W, second R
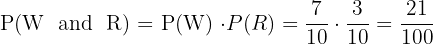
First extraction W, second W
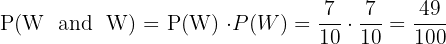
B Without replacement
In this case since there is no replacement, the extraction of the first ball modifies the conditions of the second extraction, for example if a Red ball was obtained in the first extraction, it means that in the second extraction there is one less Red ball in the urn, i.e. 2 Red balls, and also one less ball in total, i.e. 9, this means they are dependent events.
Let's see all the options
First extraction R, second R
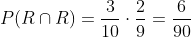
First extraction R, second W
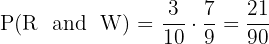
First extraction W, second R
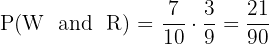
First extraction W, second W
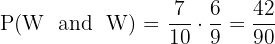
A ball is drawn from a basket containing 4 red balls, 5 white balls and 6 black balls
A What is the probability that the ball is red or white?
B What is the probability that it is not white?
A What is the probability that the ball is red or white?
Here we deal with events where there are no common elements, so we use the formula

we are left with only
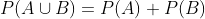
In this way, the probability that the ball is red or white is
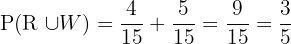
B What is the probability that it is not white?
The probability that the ball is NOT white is
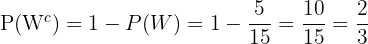
In a class there are 10 blonde female students, 20 brunette female students, 5 blonde male students and 10 brunette male students. One day 44 students attend, find the probability that the missing student:
A Is male
B Is a brunette female
C Is male or female
A Is male
In the following table we have the information from the problem
| Blonde | Brunette | Total | |
|---|---|---|---|
| Male | 5 | 10 | 15 |
| Female | 10 | 20 | 30 |
| Total | 15 | 30 | 45 |
and from here we can see that there are 15 males and 45 students, so the probability that the missing student is male is
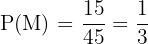
B Is a brunette female
There are 20 brunette females, so
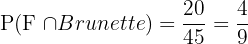
C Is male or female
Here the probability is the total
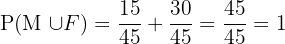
In an envelope there are 20 slips of paper, eight have a car drawn on them and the rest are blank. Find the probability of extracting at least one slip with the drawing of a car:
A If one slip is drawn
B If two slips are drawn
C If three slips are drawn
A If one slip is drawn
Since there are 8 slips with a car and 20 total slips, the probability of drawing a slip with a car is
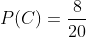
B If two slips are drawn
When drawing two slips, the outcomes can be BB, CB, BC or CC. We could calculate the probability of CB, BC, CC and then add them, but it's more practical to calculate the probability of BB and subtract the value from 1
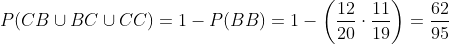
If three slips are drawn
Here we can base ourselves on the same deduction from the previous case
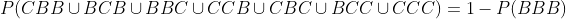
Thus
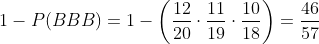
Students A and B have probabilities of failing an exam equal to 1/2 and 1/5, respectively. The probability that they both fail the exam at the same time is 1/10. Determine the probability that at least one of the two students fails the exam.
These are compatible events, meaning the probability of both happening at the same time is different from zero. We therefore calculate the probability in the following way:
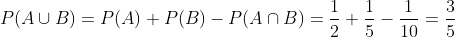
Two brothers go hunting. The first one kills an average of 2 pieces of game every 5 shots, and the second one kills 1 piece every 2 shots. If both shoot at the same time at the same piece of game, what is the probability that they kill it?
The probability that the first brother kills a piece is
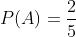
The probability that the second brother kills a piece is
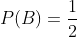
On the other hand, the probability that both kill (each hitting) at the same time is
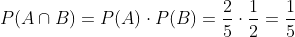
And therefore, if they shoot at the same time at the same piece and either brother A or brother B kills it, it is
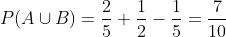
A class consists of 10 men and 20 women; half of the men and half of the women have brown eyes. Determine the probability that a randomly chosen person is a man or has brown eyes.
| Men | Women | Total | |
|---|---|---|---|
| Brown eyes | 5 | 10 | 15 |
| Other | 5 | 10 | 15 |
| Total | 10 | 20 | 30 |
Here we must observe that there are 10 men as well as 15 people with brown eyes, in addition to 5 men with brown eyes. Therefore, the probability that the person is a man or has brown eyes is calculated with the formula

So let's calculate:
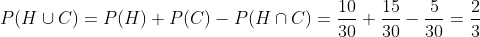
The probability that a man lives 20 years is 1/4 and that his wife lives 20 years is 1/3.
We are asked to calculate the probability:
A. That both live 20 years.
B. That the man lives 20 years and his wife does not.
C. That both die before the age of 20.
A That both live 20 years
What happens with one does not affect what happens with the other; because of this they are independent events, so we can calculate the probability as follows:
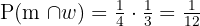
B That the man lives 20 years and his wife does not
Here they are also independent events, so we can treat them as such; we just add the formula that calculates the probability that something does not occur:
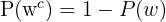
So it becomes:
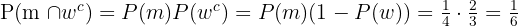
C That both die before the age of 20
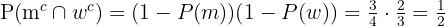
Calculate the probability of getting exactly two tails when tossing a coin four times.
The possible outcomes of a coin toss are heads (H) or tails (T).
First, we can determine the ways in which two tails (T) can appear in four tosses.
From four possible results n=4, let’s see in how many ways r=2 of them can be tails. In other words, we calculate the total number of groups of two elements (tails) that can be chosen from a total of four elements (tosses).
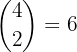
As we can see, there are 6. To be clearer, here are the 6 outcomes:
TTHH, THTH, THHT, HTTH, HTHT, HHTT
Now, the total number of possible outcomes when tossing a coin four times is:

Therefore, the probability of getting exactly two tails in four tosses is:
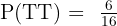
A group of 10 people sit on a bench. What is the probability that two people chosen in advance will sit together?
To know all the possible ways to arrange 10 people in 10 seats, we use permutations:

Now, to calculate the number of ways in which the 2 preselected people sit together, we can think of them as occupying a single block. In that case, they occupy one place out of nine possible. So, the number of ways in which 9 people can be seated in 9 places is:
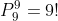
Since the two preselected people can switch places within that block (AB or BA), there are 2 possible arrangements for them. Therefore, the total number of ways in which the two chosen people can sit together is 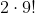
Finally, the probability that the two preselected people sit together is:
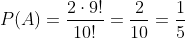
Five cards are drawn from a 52-card deck. Find the probability of drawing:
A) 4 aces
B) 4 aces and 1 king
C) 3 fives and 2 jacks
D) A 9, 10, Jack, Queen, and King in any order
E) 3 cards of one suit and 2 of another
F) At least one ace
A 4 aces
First, the total number of distinct 5-card hands, when grouping 52 cards in 5, is
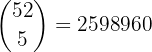
Now, from 4 aces we form one group (order doesn’t matter) of 4, giving
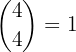
which occupies 4 of the 5 positions; and in the fifth position we can place any of the other 48 cards, so
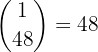
Therefore, the number of 5-card hands with 4 aces is
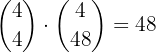
so the probability is
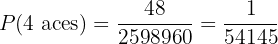
B 4 aces and a king
For 4 aces there is only one possibility, and to have a king there are four possibilities. In other words, we multiply the possibilities for 4 aces by those for the king:
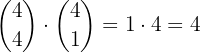
Hence, the probability is
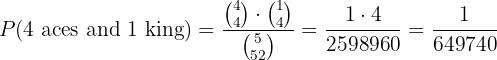
C 3 fives and 2 jacks
There are 4 fives and we want 3 of them; and there are 4 jacks and we want 2 of them, so
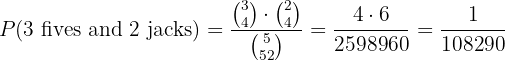
D A 9, 10, Jack, Queen, and King in any order
For each rank there are 4 possibilities, and since there are 5 cards we have 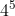
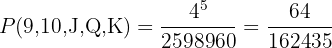
E 3 of one suit and 2 of another
To have 3 of one suit (13 cards) we compute

since there are 4 suits
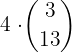
is the total number of ways to get 3 cards of a suit. The same reasoning for the other two cards, but now we only have 3 suits left, so we use
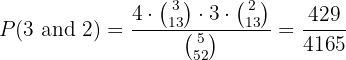
F At least one ace
First, compute the probability of no ace; that is, we remove all the aces:
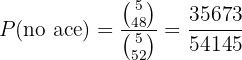
And then the probability of at least one ace is the remainder: