Radicals are a fundamental concept in algebra, used to express roots of numbers and variables. Mastering the handling of radicals is essential for advancing in mathematics, as they apply to a wide variety of problems, from simplifying expressions to solving more complex equations.
In this set of solved exercises, we will explore different types of problems related to radicals. Each exercise is designed to reinforce your knowledge and skills in manipulating radical expressions, including simplification, rationalizing denominators, and radical powers.
Calculate the values of the following rational powers:
1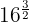
2
3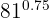
4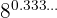
A power with a fractional exponent equals a root whose index is the denominator of the fraction and the exponent of the radicand is the numerator.
To solve, we first decompose the radicand into factors, perform the operations on the radicand and extract factors
1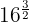
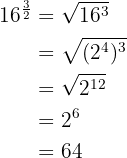
2
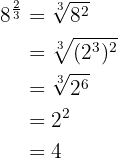
3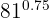
In this case we convert the exponent that is an exact decimal number to a fraction
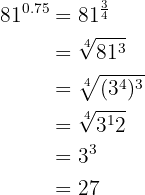
4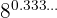
We convert to a fraction the exponent that is a pure repeating decimal
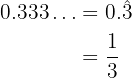
Once we know the exponent as a fraction, we solve
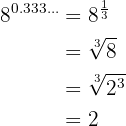
Extract factors in the following radicals:
1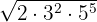
2
1 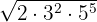
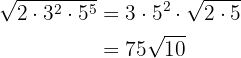
The exponent of two  is less than the index
is less than the index  , therefore it remains in the radicand.
, therefore it remains in the radicand.
The exponent of 
 equals the index
equals the index  , therefore the
, therefore the  comes out of the radicand.
comes out of the radicand.
The exponent of 
 is greater than the index
is greater than the index  , therefore this exponent is divided by the index. The quotient obtained
, therefore this exponent is divided by the index. The quotient obtained  is the exponent of the factor outside the radicand and the remainder
is the exponent of the factor outside the radicand and the remainder  is the exponent of the factor inside the radicand.
is the exponent of the factor inside the radicand.
2 
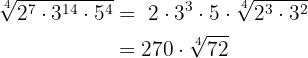
The exponents are greater than the index, therefore these exponents are divided by the index.
Each of the quotients obtained will be the exponent of the corresponding factor outside the radicand and each of the remainders obtained will be the exponent of the corresponding factor inside the radicand.
Introduce all factors into the radicals:
1 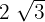
2
1 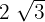
Before we begin solving, let's remember some properties of radicals. We know that the radical applied to a product is the product of the radicals
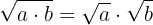
and that the index of the radical when converted to exponential form divides the power of the base

then these two results together we use to simplify expressions with radicals multiplied by factors, that is
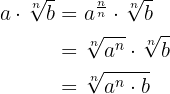
and thus we can simply use the result

Let's now apply this process to our problem:
We introduce the  raised to the index of the radical
raised to the index of the radical  and perform the operations
and perform the operations
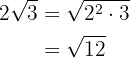
2
We introduce the factors raised to the index 
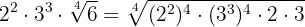
We perform the operations
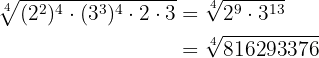
Convert the following radicals to a common index:
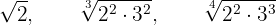
We find the least common multiple of the indices, which will be the common index
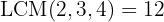
We divide the common index by each of the indices and each result obtained is multiplied by its corresponding exponents
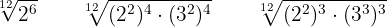
We perform the operations in the radicals
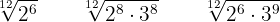
Perform the following radical additions:
1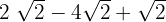
2
3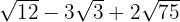
4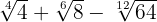
1 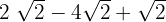
Since the radicals are like terms, we add the coefficients of the radicals:
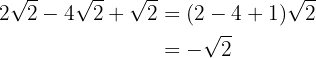
2 
We add the coefficients of the radicals:
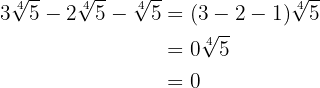
3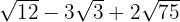
We decompose the radicands into factors and extract factors from the radicals (if possible) and multiply them by the coefficient of the corresponding radical
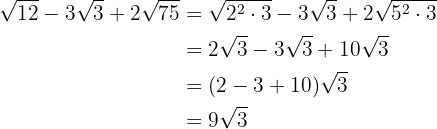
4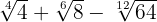
We extract factors from the radicals and multiply them by the coefficient of the corresponding radical

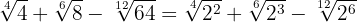
We simplify the radicals. In the first radical we divide the index and the exponent of the radicand by  , in the second by
, in the second by  and in the third by
and in the third by 
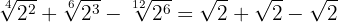
We add the coefficients of the radicals
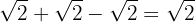
Find the sums of radicals by converting to the same index:
1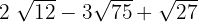
2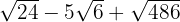
3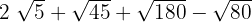
4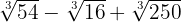
To perform these sums of unlike radicals, we will follow these two steps:
We decompose the radicals into factors and extract factors from the radicals (if possible) and multiply them by the coefficient of the corresponding radical
We add the coefficients of the radicals
1 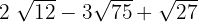
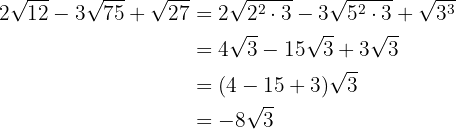
2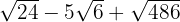
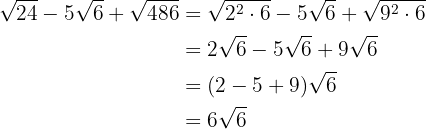
3 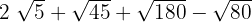
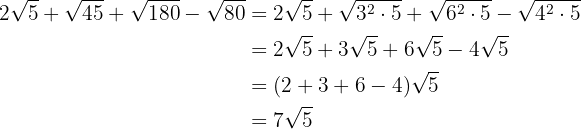
4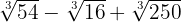
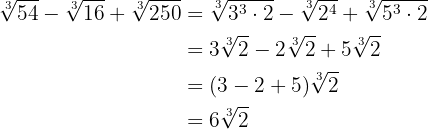
Perform the following radical additions:
1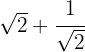
2
1
We rationalize the second term by multiplying and dividing by the square root of 
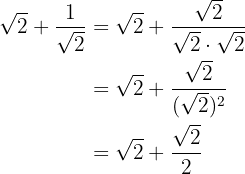
We factor out the common factor of square root of  and add
and add
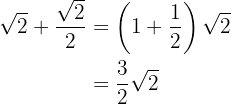
2 
We decompose the radicals into factors

In the first two terms we extract factors, the third we simplify the radical by dividing the index and the exponent of the radicand by  and the last we will rationalize by multiplying and dividing by the cube root of
and the last we will rationalize by multiplying and dividing by the cube root of 
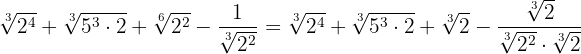
Since all the radicals are like terms we can add their coefficients
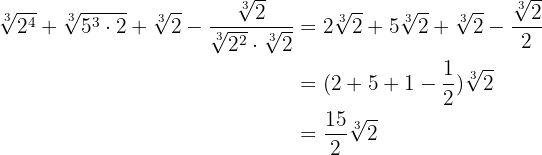
Perform the following radical products:
1
2
3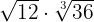
1 
Since the radicals have the same index we multiply the radicands and decompose into factors to extract factors from the radical.
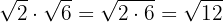
2 
We decompose the radicands into factors
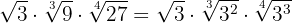
We reduce to a common index so we need to calculate the least common multiple of the indices, which will be the common index.
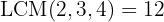
We divide the common index  by each of the indices
by each of the indices  and each result obtained is multiplied by its corresponding exponents
and each result obtained is multiplied by its corresponding exponents  .
.
We perform the product of powers with the same base in the radicand and extract factors from the radicand
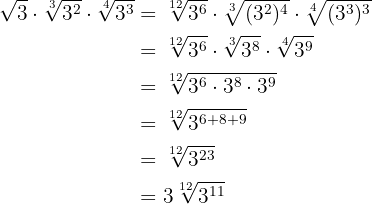
3 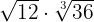
We calculate the least common multiple of the indices.
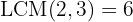
Let's proceed with the calculations:
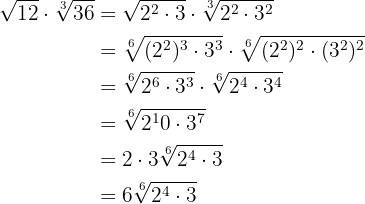
Perform the following radical divisions:
1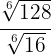
2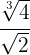
3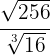
1 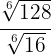
Since the radicals have the same index we divide the radicands and simplify the radical by dividing the index and exponent of the radicand by 
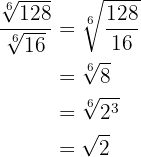
2 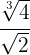
First we reduce to a common index so we need to calculate the least common multiple of the indices, which will be the common index.
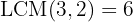 .
.
We divide the common index  by each of the indices
by each of the indices 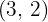 and each result obtained is multiplied by its corresponding exponents
and each result obtained is multiplied by its corresponding exponents 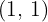 .
.
We decompose  into factors to be able to perform the division of powers with the same base and divide.
into factors to be able to perform the division of powers with the same base and divide.
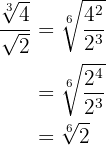
3 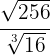
We perform the same steps as in the previous exercise
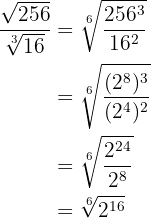
We simplify the radical by dividing the index and the exponent of the radicand by  , and finally extract factors
, and finally extract factors
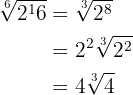
Simplify the following operation

First we calculate the least common multiple of the indices, which will be the common index
We divide the common index  by each of the indices
by each of the indices  and each result obtained is multiplied by its corresponding exponents
and each result obtained is multiplied by its corresponding exponents 
We remove the parentheses, simplify the fraction and multiply the powers with the same base in the numerator
We simplify the radical by dividing the index and the exponent of the radicand by 
Finally we extract factors

Simplify to a single radical
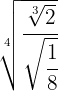
First, let's note that  , therefore
, therefore
We put the roots in the numerator and denominator to a common index.
We cube the denominator and perform the division of powers with the same base.
We take the fourth root of the radical by multiplying the indices.
Perform the operations with powers:
1
2
1 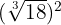
We raise the radicand to the second power, decompose  into factors and raise them to the second power and finally extract factors
into factors and raise them to the second power and finally extract factors
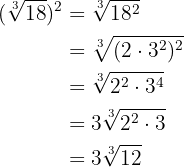
2 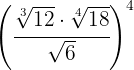
We raise the radicands to the fourth power, decompose the radicands into factors and extract  from the radical
from the radical
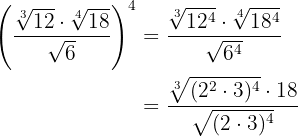
In the radicands we perform the operations with powers and convert to a common index to be able to perform the division
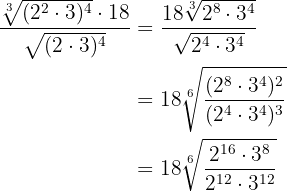
We simplify the radical by dividing the index and the exponents of the radicand by  and perform a division of powers with the same exponent
and perform a division of powers with the same exponent
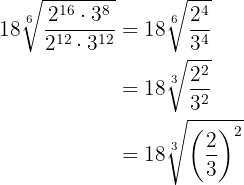
We can rationalize by multiplying and dividing by the cube root of 
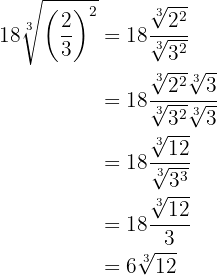
Perform the binomial operations with radicals:
1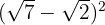
2
3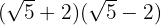
4
1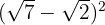
A difference squared equals the square of the first, minus twice the first times the second, plus the square of the second
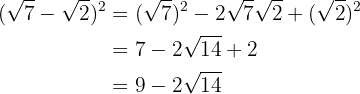
2
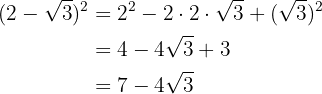
3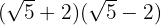
A sum times a difference equals the difference of squares
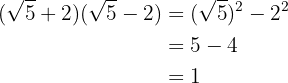
4
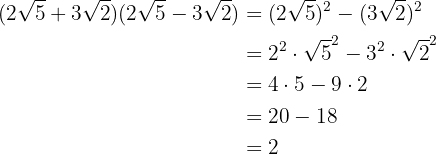
Perform the following mixed operations with radicals:
1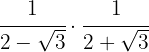
2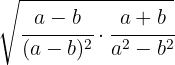
1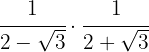
We perform the multiplication of fractions, in the denominator we have a sum times a difference which equals the difference of squares
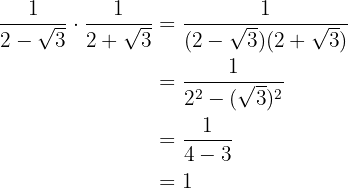
2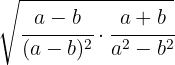
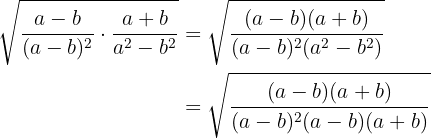
The difference of squares in the denominator is written as a sum times a difference and the fraction is simplified
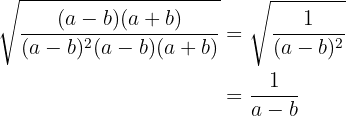
Perform the following operations with nested radicals:
1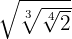
2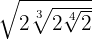
3
1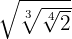
We multiply the indices
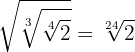
2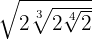
We introduce the first  inside the cube root so we have to cube it and multiply the powers with the same base, we continue this procedure until all values have been introduced into the radicals, and with this, we multiply
inside the cube root so we have to cube it and multiply the powers with the same base, we continue this procedure until all values have been introduced into the radicals, and with this, we multiply  and then we get
and then we get 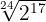 .
.
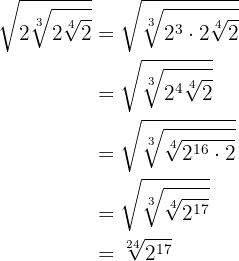
3
We introduce the  inside the square root by squaring it.
inside the square root by squaring it.
We multiply the powers with the same base.
We multiply the indices and simplify by dividing the resulting index and the exponent of the radicand by 3.
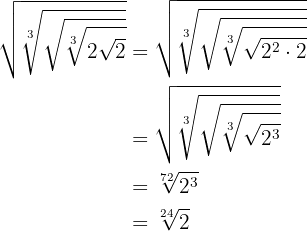
Rationalize the radicals:
1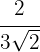
2
3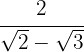
4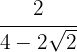
5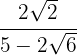
1 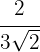
We multiply the numerator and the denominator by the square root of  , perform the calculations and simplify the fraction.
, perform the calculations and simplify the fraction.
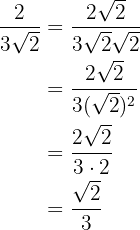
2
We write the radicand  in power form:
in power form:  .
.
We have to multiply in the numerator and denominator by the fifth root of  .
.
We multiply the radicals in the denominator, extract factors from the radical and simplify the fraction.
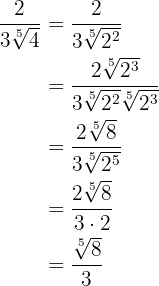
3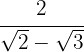
We multiply the numerator and the denominator by the conjugate of the denominator, remove parentheses in the numerator and perform the sum times difference in the denominator, obtaining a difference of squares.
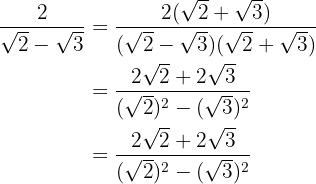
In the denominator we extract the radicands and divide by  , that is, we change the sign of the numerator.
, that is, we change the sign of the numerator.
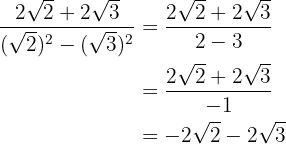
4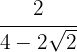
We multiply and divide the fraction by the conjugate of the denominator.
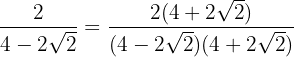
We perform the sum times difference in the denominator, obtaining a difference of squares and operate:
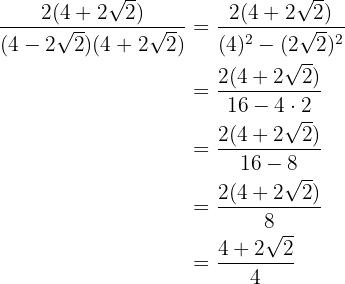
5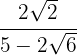
We multiply the numerator and the denominator by the conjugate of the denominator, remove parentheses in the numerator and perform the sum times difference in the denominator, obtaining a difference of squares.
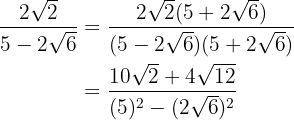
In the numerator we decompose  into factors and extract factors, we finish by performing the operations in the denominator.
into factors and extract factors, we finish by performing the operations in the denominator.
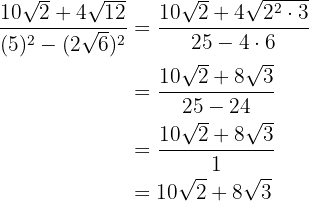
Rationalize the following radicals:
1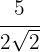
2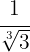
3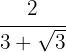
4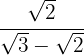
5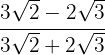
1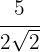
We multiply the numerator and the denominator by the square root of  and perform the calculations
and perform the calculations
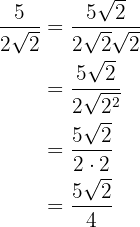
2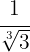
Here we realize that to eliminate the radical  we need to generate the product
we need to generate the product
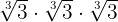
so that the radical is eliminated, that is
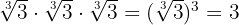
in other words, since we already have  in the denominator, we only need to multiply it by
in the denominator, we only need to multiply it by  to eliminate the radical.
to eliminate the radical.
So as to not affect the numerical value of the expression, we multiply  in both the numerator and denominator, and this is how our development looks
in both the numerator and denominator, and this is how our development looks
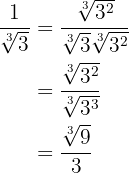
3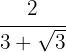
We multiply and divide the fraction by the conjugate of the denominator.
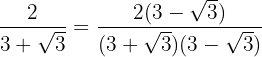
In the numerator we remove parentheses and in the denominator we perform the sum times difference, obtaining a difference of squares.
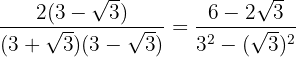
We perform the operations and simplify the fraction by factoring out 
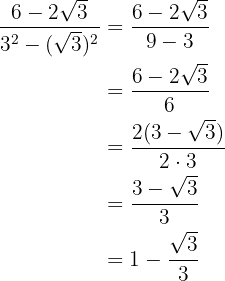
4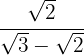
We multiply and divide the fraction by the conjugate of the denominator
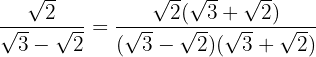
In the numerator we remove parentheses and in the denominator we perform the sum times difference, obtaining a difference of squares
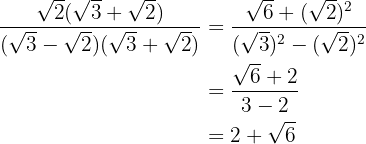
5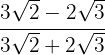
We multiply the numerator and the denominator by the conjugate of the denominator

We write the numerator in power form

In the numerator we have a difference squared which equals the square of the first, minus twice the first times the second, plus the square of the second. In the denominator we have a sum times difference which equals the difference of squares

We perform the operations and simplify at the end
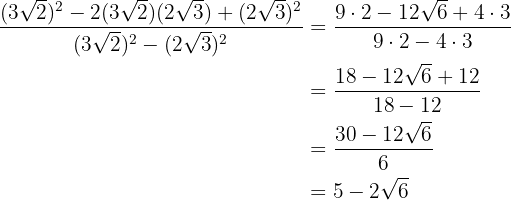
Looking to boost your math skills? Superprof connects you with amazing tutors who can help you conquer radicals and beyond - whether you prefer learning online or having a teacher come to you!


