Chapters
Properties and Operations with Radicals
A radical is an expression of the form 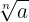 , where
, where 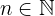 and
and 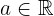 . Additionally, if
. Additionally, if 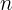 is even, then
is even, then  cannot be negative
cannot be negative 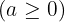 .
.
For example, we have that  is even. Therefore,
is even. Therefore, 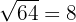 ; while
; while 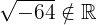 .
.
Likewise, since  is odd, then
is odd, then 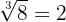 and
and 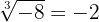 . That is, the cube root is defined for any real number.
. That is, the cube root is defined for any real number.
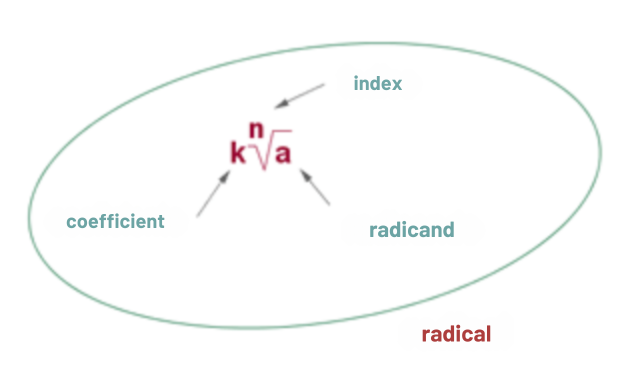
The parts that make up a radical are: coefficient, index and radicand.
Powers and Radicals
A radical can be expressed in the form of a power:
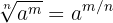

Equivalent Radicals
Using fractional exponent notation and the property of fractions that states that if you multiply numerator and denominator by the same number the fraction is equivalent, we obtain that:
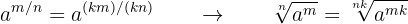
If the index and the exponent or exponents of the radicand are multiplied or divided by the same natural number, another equivalent radical is obtained.
Simplification of Radicals
If there exists a natural number that divides the index and the exponent (or exponents) of the radicand, a simplified radical is obtained.
Reduction to Common Index
To reduce two or more radicals to a common index:
1 We find the least common multiple of the indices, which will be the common index
2 We divide the common index by each of the indices and each result obtained is multiplied by its corresponding exponents
Extraction of Factors in a Radical
To extract factors from a radical, the radicand is decomposed into factors. If:
1 An exponent of the radicand is less than the index:
The corresponding factor is left in the radicand.
2 An exponent of the radicand is equal to the index:
The corresponding factor comes out of the radicand.
3 An exponent of the radicand is greater than the index:
Said exponent is divided by the index. The quotient obtained is the exponent of the factor outside the radicand and the remainder is the exponent of the factor inside the radicand.
Introduction of Factors in a Radical
To introduce factors into a radical, the factors are raised to the index of the radical.
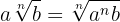
Operations with Radicals
For radicals we have the operations of addition, subtraction, multiplication, division and others that we will see below:
1 Addition and Subtraction of Radicals
Only two radicals can be added (or subtracted) when they are similar radicals, that is, if they are radicals with the same index and equal radicand.
To add radicals with the same index and equal radicand, the coefficients of the radicals are added.

2 Multiplication of Radicals
In multiplication we have two cases: with the same index or with different index.
a) Multiplication of radicals with the same index.
To multiply radicals with the same index, multiply the radicands and keep the same index.

b) Multiplication of radicals with different index.
First they are reduced to a common index and then multiplied.
3 Division of Radicals
In division we have two cases: with the same index or with different index.
a) Division of radicals with the same index.
To divide radicals with the same index, divide the radicands and keep the same index.
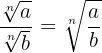
b) Division of radicals with different index.
First they are reduced to a common index and then divided.
4 Power of a Radical
To raise a radical to a power, the radicand is raised to that power and the same index is kept.
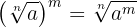
5 Rationalization
It consists of removing radicals from the denominator, which allows facilitating the calculation of operations such as addition of fractions.
We can distinguish three cases:
a) Rationalization of the type 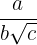
Multiply the numerator and denominator by 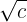

b) Rationalization of the type 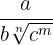
Multiply numerator and denominator by 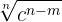
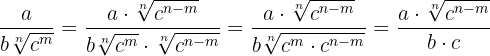
c) Rationalization of the type 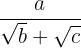 and in general when the denominator is a binomial with at least one radical.
and in general when the denominator is a binomial with at least one radical.
Multiply the numerator and denominator by the conjugate of the denominator.
The conjugate of a binomial is equal to the binomial with the central sign changed:
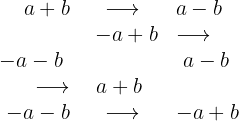
We also have to keep in mind that: "sum times difference equals difference of squares".
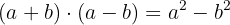
Exercises with Radicals
Write in power form 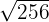
We put the radicand in power form

The index of the radical  becomes the denominator and the exponent of the radicand
becomes the denominator and the exponent of the radicand 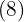 becomes the numerator and we perform the operations:
becomes the numerator and we perform the operations:
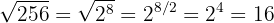
An equivalent radical of  is
is 
We multiply the index and the exponent of the radicand by a positive integer, for example 
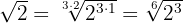
Simplify:
1 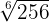
2 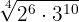
1 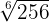
We put  in power form
in power form

To simplify the radical we divide both the index  and the exponent of the radicand
and the exponent of the radicand 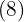 by
by 
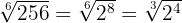
2 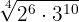
To simplify the radical we divide the index  and the exponents of the radicand
and the exponents of the radicand 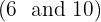 by
by 
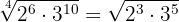
Put the radicals to common index: 
First we find the l.c.m. of the indices: 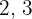 and
and 
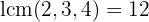
We divide the common index by each of the indices
by each of the indices 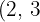 and
and 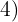 and each result obtained is multiplied by its corresponding exponents
and each result obtained is multiplied by its corresponding exponents

We operate with the powers

Verify if it is possible to extract the factors of:
1 
2 
1 
Since 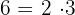 and the exponents of the factors is 1, which is less than index 2; thus
and the exponents of the factors is 1, which is less than index 2; thus
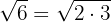
2 
Since 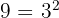 and the exponent 2 is less than index 3; thus
and the exponent 2 is less than index 3; thus

Extract the factors of:
1 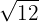
2 
1 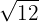
We decompose  into factors, since
into factors, since  is raised to the same power as the index we can extract
is raised to the same power as the index we can extract  from the radicand; thus we obtain
from the radicand; thus we obtain

2 
We decompose  into factors, since
into factors, since  is raised to the same power as the index we can extract
is raised to the same power as the index we can extract  from the radicand; thus we obtain
from the radicand; thus we obtain
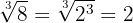
Extract the factors of:
1 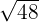
2 
3 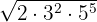
4 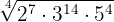
1 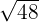
The exponent of 2 is greater than the index, therefore said exponent  is divided by the index
is divided by the index 
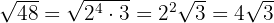
The quotient obtained  is the exponent of the factor outside the radicand and the remainder
is the exponent of the factor outside the radicand and the remainder 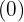 is the exponent of the factor inside the radicand.
is the exponent of the factor inside the radicand.
Since the factor  equals 1, it is not necessary to place it in the radicand since if it is multiplied by another factor it does not change
equals 1, it is not necessary to place it in the radicand since if it is multiplied by another factor it does not change
In general, if dividing the exponent of a factor by the index gives remainder zero, we will not place that factor in the radicand
2 
We decompose into factors: 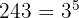
The exponent is greater than the index, therefore said exponent  is divided by the index
is divided by the index 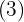 .
.
The quotient obtained  is the exponent of the factor outside the radicand and the remainder
is the exponent of the factor outside the radicand and the remainder  is the exponent inside the radicand
is the exponent inside the radicand

3 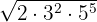
There are exponents in the radicand greater than the index, therefore said exponents 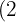 and
and 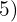 are divided by the index
are divided by the index  .
.
Each of the quotients  and
and  obtained will be the exponent of the corresponding factor outside the radicand and each of the remainders obtained
obtained will be the exponent of the corresponding factor outside the radicand and each of the remainders obtained  and
and  will be the exponents of the corresponding factors inside the radicand
will be the exponents of the corresponding factors inside the radicand

4 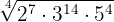
The exponents in the radicand are greater than the index, therefore said exponents  and
and 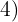 are divided by the index
are divided by the index  .
.
Each of the quotients 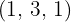 obtained will be the exponent of the corresponding factor outside the radicand and each of the remainders obtained
obtained will be the exponent of the corresponding factor outside the radicand and each of the remainders obtained 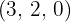 will be the exponents of the corresponding factors inside the radicand
will be the exponents of the corresponding factors inside the radicand

Introduce the factors into the radical:
1 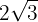
2 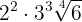
1 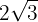
Since the index is  , the factor outside the radical
, the factor outside the radical  is squared and we perform the operations
is squared and we perform the operations
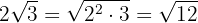
2 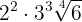
Both  and
and  are introduced raised to the fourth power, that is,
are introduced raised to the fourth power, that is,
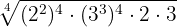
We remove the parentheses by multiplying the exponents and multiply the powers with the same base

Perform the sums:
1 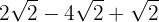
2 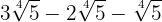
3 
4 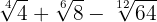
5 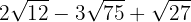
6 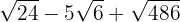
7 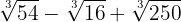
8 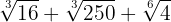
1 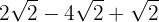
We add and subtract (depending on the signs) the coefficients of the radicals and we have
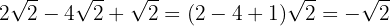
2 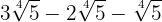
We add the coefficients of the radicals
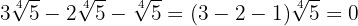
3 
We decompose the radicands into factors:

So the roots are
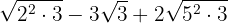
We extract factors from the radicals and multiply them by the coefficient of the corresponding radical
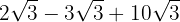
We add the coefficients of the radicals
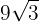
4 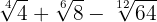
We extract factors from the radicals and multiply them by the coefficient of the corresponding radical
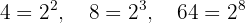
So that
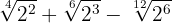
We simplify the radicals. In the first radical we divide the index and the exponent of the radicand by  , in the second by
, in the second by  and in the third by
and in the third by 
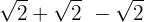
We add the coefficients of the radicals
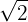
5 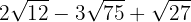
We express the radicands in factors
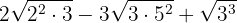
We extract factors from the radicand
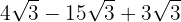
We add the coefficients and we have
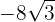
6 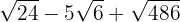
We express the radicands in factors
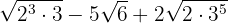
We extract factors from the radicand
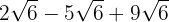
We add the coefficients and we have

7 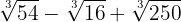
We express the radicands in factors
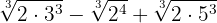
We extract factors from the radicand
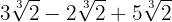
We add the coefficients and we have

8 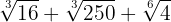
We express the radicands in factors
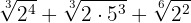
We extract factors from the radicand
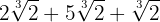
We add the coefficients and we have
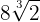
Perform the multiplication 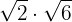
We multiply the radicands
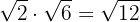
When we finish performing an operation we will extract factors from the radical, if possible.
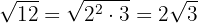
Perform the multiplications:
1 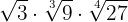
2 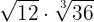
1 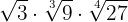
We decompose the radicands into factors

We reduce to common index so we have to calculate the least common multiple of the indices, which will be the common index.
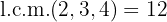
We divide the common index  by each of the indices
by each of the indices  and each result obtained is multiplied by its corresponding exponents
and each result obtained is multiplied by its corresponding exponents  . We perform the product of powers with the same base in the radicand and extract factors from the radicand.
. We perform the product of powers with the same base in the radicand and extract factors from the radicand.

2 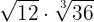
We calculate the least common multiple of the indices
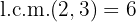
We divide the common index  by each of the indices
by each of the indices 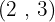 and each result obtained is raised to the corresponding radicands
and each result obtained is raised to the corresponding radicands
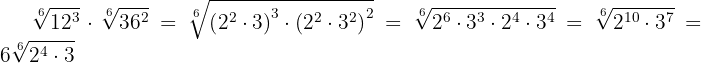
We decompose  and
and  into factors, perform operations with powers and extract factors
into factors, perform operations with powers and extract factors
Perform the division 
Since both radicals have the same index we put everything in one radical with the same index
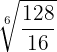
We decompose into factors, perform division of powers with the same base

We simplify the radical by dividing the index and the exponent of the radicand by 
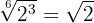
Perform the divisions:
1 
2 
3 
1 
First we reduce to common index so we have to calculate the least common multiple of the indices, which will be the common index 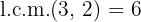 .
.
We divide the common index  by each of the indices (
by each of the indices ( and
and  ) and each result obtained is multiplied by its corresponding exponents (
) and each result obtained is multiplied by its corresponding exponents ( and
and  )
)
2 
We decompose  into factors to be able to perform division of powers with the same base and divide
into factors to be able to perform division of powers with the same base and divide
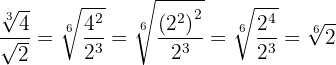
3 
We perform the same steps as the previous example

We simplify the radical by dividing the index and the exponent of the radicand by  , and finally extract factors
, and finally extract factors
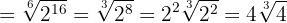
Simplify:
1 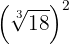
2 
1 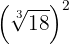
We raise the radicand to the power of two, decompose  into factors and raise them to the power of two and finally extract factors
into factors and raise them to the power of two and finally extract factors
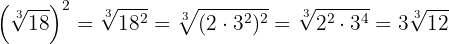
2 
We raise the radicands to the fourth power, decompose the radicands into factors and extract  from the radical
from the radical
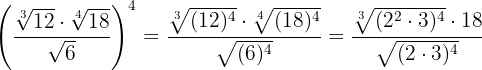
In the radicands we perform operations with powers and put to common index to be able to perform the division
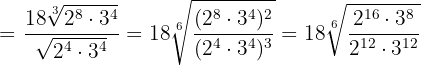
We simplify the radical by dividing the index and the exponents of the radicand by  and perform a division of powers with the same exponent
and perform a division of powers with the same exponent
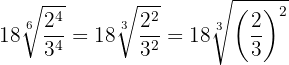
Simplify:
1 
2 
1 
We multiply the indices
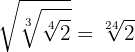
2 
We introduce the first  inside the cube root so we have to cube it and multiply the powers with the same base
inside the cube root so we have to cube it and multiply the powers with the same base
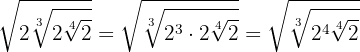
We introduce  in the fourth root so we have to raise it to the fourth power, perform the product of powers and finally the product of the indices
in the fourth root so we have to raise it to the fourth power, perform the product of powers and finally the product of the indices

Rationalize 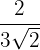
We multiply the numerator and denominator by 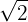
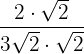
We simplify
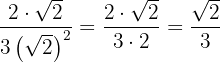
Rationalize 
The radicand  we put in power form:
we put in power form: 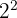
We have to multiply in the numerator and denominator by the fifth root of 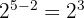
We multiply the radicals in the denominator, extract factors from the radical and simplify the fraction

Rationalize:
1 
2 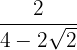
3 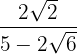
1 
We multiply numerator and denominator by the conjugate of the denominator, remove parentheses in the numerator and perform the sum times difference in the denominator, so we obtain a difference of squares
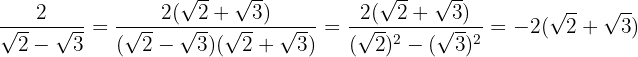
2 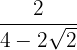
We multiply and divide the fraction by the conjugate of the denominator
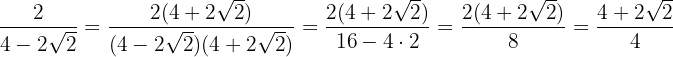
3 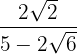
We multiply numerator and denominator by the conjugate of the denominator, remove parentheses in the numerator and perform the sum times difference in the denominator, so we obtain a difference of squares
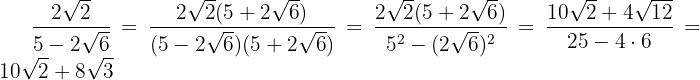
Do you need private math classes? Don't hesitate and check out Superprof to look for an instructor. On our page you can find both online and in-person teachers!












