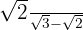Welcome to the real numbers exercises! Real numbers are fundamental in mathematics and encompass a wide range of values, including whole numbers, fractions, decimals, rational and irrational numbers. These numbers extend infinitely in both directions and are the foundation for performing essential mathematical operations.
Throughout this series of exercises, you will test your skills in different concepts related to real numbers. Remember that real numbers are a powerful tool for representing quantities and magnitudes in everyday life and in various academic and professional fields. Furthermore, their study is essential for understanding more advanced concepts in mathematics and sciences.
Go ahead! Dive into the exercises and enjoy reinforcing your skills with real numbers.
Classify the numbers:
a 
b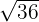 
c 
d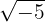 
e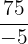 
a
Note that is an irrational number, that is, , where represents the rational numbers. It is known that the product, division, sum, or difference between an irrational number and a rational number is an irrational number, therefore, we have that is irrational
b 
Observe that we can solve this root exactly, that is,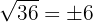 
, where 
and 
are integers, therefore
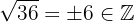
c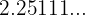
Every number that has a repeating decimal can be expressed as a fraction, which means that every number with a repeating decimal is a rational number. In fact, we have that which proves that it is a rational number
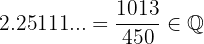
d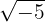
The square roots of negative numbers have never belonged to the real numbers; these numbers belong to an extension of the real numbers known as the complex numbers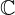 
. Given the above, this number is a complex number.
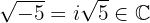
e
Having a fraction between integers, it is clear that we have a rational number, however, if we perform the division, we have that this fraction is equivalent to the integer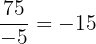 
. Given the above, we have that
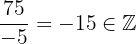
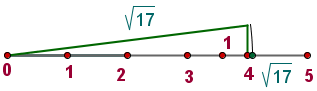
Represent on the number line: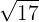 
To find it, first note that when calculating the square root, we have that
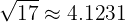
Let's graph this point on the number line
Represent on the real number line the numbers that satisfy the following relations:
a)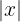 
< 
b) 
c)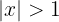 
d)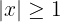 
a <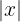
Note that by definition of absolute value, the following inequalities are equivalent
where the last inequality implies that 
.
b
Note that by definition of absolute value, the following inequalities are equivalent
where the last inequality implies that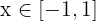 
.
c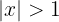
Note that by definition of absolute value, the following inequalities are equivalent
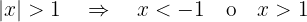
where the last inequality implies that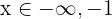 
or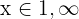 
, which we can express in terms of the union of sets as 
.
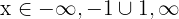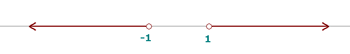
d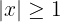
Note that by definition of absolute value, the following inequalities are equivalent
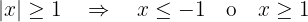
where the last inequality implies that 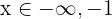or 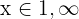, which we can express in terms of the union of sets as .
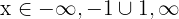Calculate the values of the following powers:
a 
b 
c 
d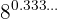 
a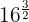 
A power with a fractional exponent is equal to a root whose index is the denominator of the fraction 
and the exponent of the radicand is the numerator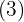 
.
We decompose 16 into factors, perform the operations on the radicand, and extract factors:
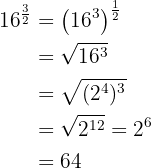
b 
A power with a fractional exponent is equal to a root whose index is the denominator of the fraction 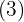and the exponent of the radicand is the numerator .
We decompose 8 into factors, perform the operations on the radicand, and extract factors:
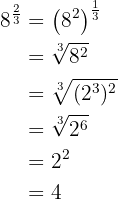
c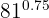 
In this case we convert the exponent, which is a terminating decimal, to a fraction:
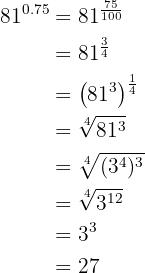
d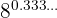 
The exponent is a pure repeating decimal, therefore we can express it as a fraction: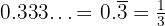 
. Therefore
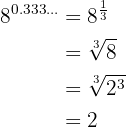
Find the sums:
a)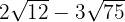 
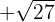
b)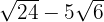 
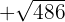
c)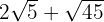 
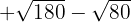
d)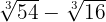 
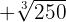
We will solve the exercises simply by decomposing the radicand into powers of prime numbers. Then with simple algebra, addition, and subtraction, we will solve the problems.
a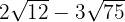
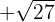
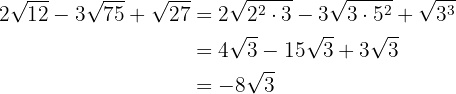
b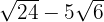
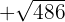
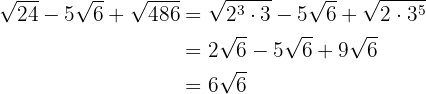
c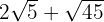
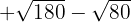
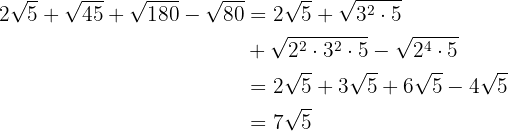
d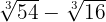
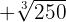
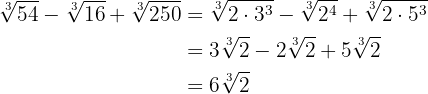
Perform the operations:
a)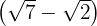 
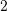
b)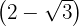 
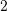
c)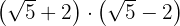 
d)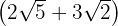 
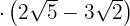
To solve this exercise we will simply apply the theory we know about powers and multiplication of binomials
a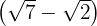
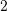
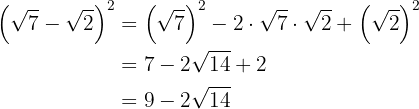
b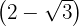
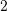
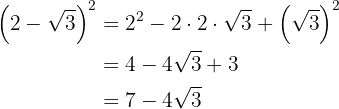
c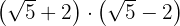
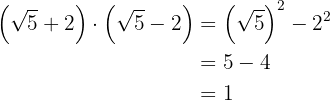
d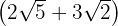
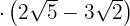
Operate: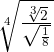 
To solve this exercise we will apply much of the exponent theory we know. We will work with the fractions in the exponents until we simplify our expression appropriately
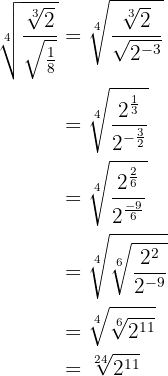
Perform: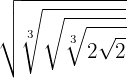 
To solve this exercise we will apply the equivalence of fractional powers with radicals to simplify:
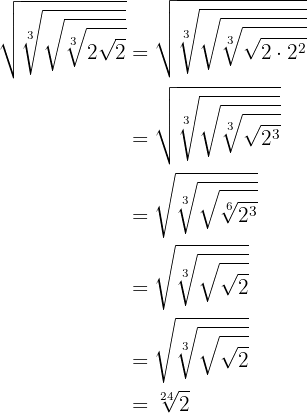
Calculate:
a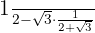 
b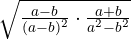 
We will use what we know about algebra to perform these operations:
a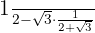
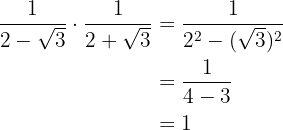
b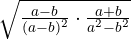
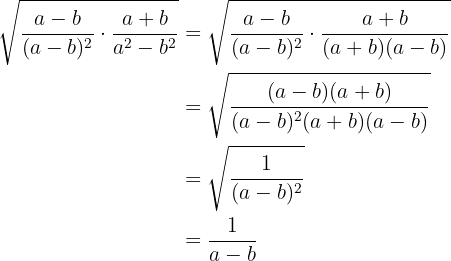
Rationalize:
a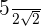 
b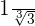 
c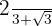 
d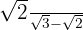 
Remember that rationalizing consists of eliminating radicals from the denominator of a fraction. To do this, we multiply the fraction by an appropriate multiplicative identity of one.
a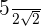
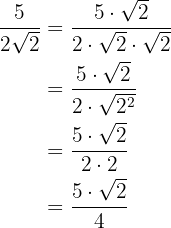
b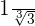
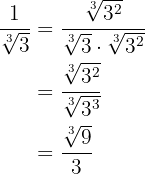
c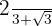
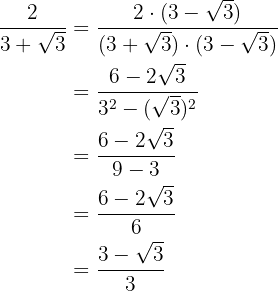
d
Did you like this article? Rate it!
Loading...
