Steps of the Elimination Method
To solve a system of equations by the elimination method we will follow these steps:
1 Prepare the two equations, multiplying them by a number such that the resulting equations have a common coefficient
2 Perform a subtraction (or addition depending on the case of the signs of the coefficients) to eliminate one of the unknowns
3 Solve the resulting equation
4 The value obtained is substituted into one of the initial equations and solved
5 The two values obtained constitute the solution of the system
Examples of the Elimination Method
In this case, there are two ways to solve the following system of equations.
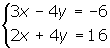
By Multiplication
1 We eliminate x by multiplying the first equation by 2 and the second by −3
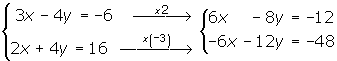
2 To the top equation, we add the bottom equation and solve the equation.
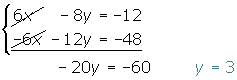
3 We substitute the value of y into either of the 2 initial equations, in this case the second.
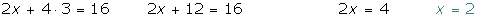
4 The solution is:
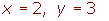
Adding (or Subtracting) the Equations Directly
Since this equation allows us to eliminate 
without needing multiplication, we can add the equations without preparing them as in the previous method.
1 We add the equations member by member:
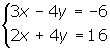
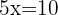
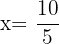
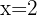
2 We substitute the value of x into either of the 2 initial equations, in this case the first.
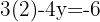
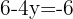
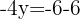
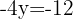
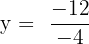
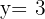
We can observe that in both cases, the solutions are the same.
Did you like this article? Rate it!
Loading...
