Throughout this article, you will find a series of solved problems that will allow you to better understand the behavior and applications of right triangles. The problems will address topics such as the use of relationships between trigonometric ratios (sine, cosine, and tangent) and the calculation of unknown lengths and angles. With each solved exercise, you will reinforce key concepts so that you develop practical skills to face a variety of geometric situations.
Solve the following exercises:
In a right triangle  , we have the following information: the hypotenuse is
, we have the following information: the hypotenuse is 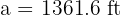 and one of the legs is
and one of the legs is 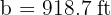 . Solve the triangle.
. Solve the triangle.
Solving the triangle means finding the length of the missing side and the value of all angles in it. Note that since it is a right triangle, we know that angle 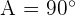 .
.
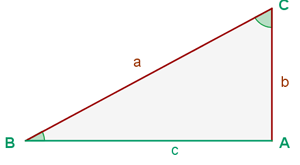
Applying sine we have:
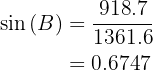
Applying arcsine we have:
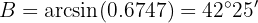
Now, once we have two angles, we can immediately calculate the last one:

Applying cosine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
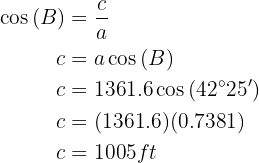
Thus we have obtained the missing data.
In a right triangle  , the legs are known:
, the legs are known: 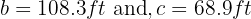 . Solve the triangle.
. Solve the triangle.
Solving the triangle means finding the missing sides and angles. Note that since it is a right triangle, we also have angle  .
.
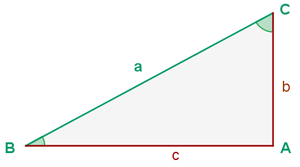
To find angle  we will calculate its tangent and then apply arctangent:
we will calculate its tangent and then apply arctangent:
Then, applying arctangent we have 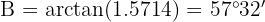 . Now, with this we have two angles, so we can directly calculate the third,
. Now, with this we have two angles, so we can directly calculate the third,  :
:
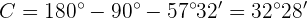
Finally, to obtain the value of side  we will use the sine formula and apply it to angle
we will use the sine formula and apply it to angle  , then solve for
, then solve for  to find its value:
to find its value:
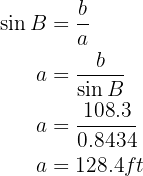
Thus, we have obtained the missing data.
In a right triangle  , the hypotenuse and one of the angles are known, whose values are
, the hypotenuse and one of the angles are known, whose values are 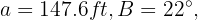 respectively. Solve the triangle.
respectively. Solve the triangle.
Solving a triangle means finding the missing sides and angles. Note that being a right triangle implies that 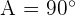 .
.
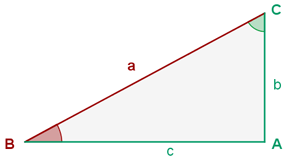
By knowing two of the three angles, we can directly obtain the third,  :
:
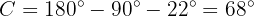
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
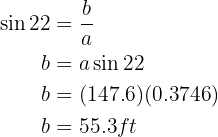
To obtain side  we will apply cosine to angle
we will apply cosine to angle  and solve for
and solve for  :
:
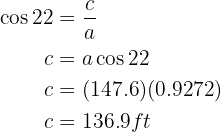
Thus, we have found the missing sides and angles.
In a right triangle  , a leg and an angle are known:
, a leg and an angle are known: 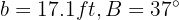 . Solve the triangle.
. Solve the triangle.
Let's obtain the missing sides and angles. Note that since it is a right triangle, we already know angle 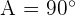 .
.
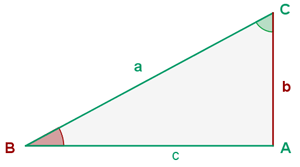
Since we already know two of the three angles, we can calculate the missing one,  , directly:
, directly:
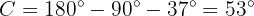
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
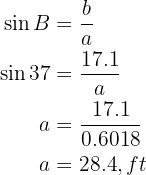
To obtain side  we will apply cotangent to angle
we will apply cotangent to angle  and solve for
and solve for  :
:
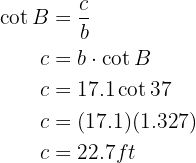
We have found the missing sides and angles.
In a right triangle  , the hypotenuse and an angle are known:
, the hypotenuse and an angle are known: 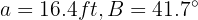 . Solve the triangle.
. Solve the triangle.
Let's obtain the missing sides and angles. Note that since it is a right triangle, we already know angle 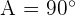 .
.
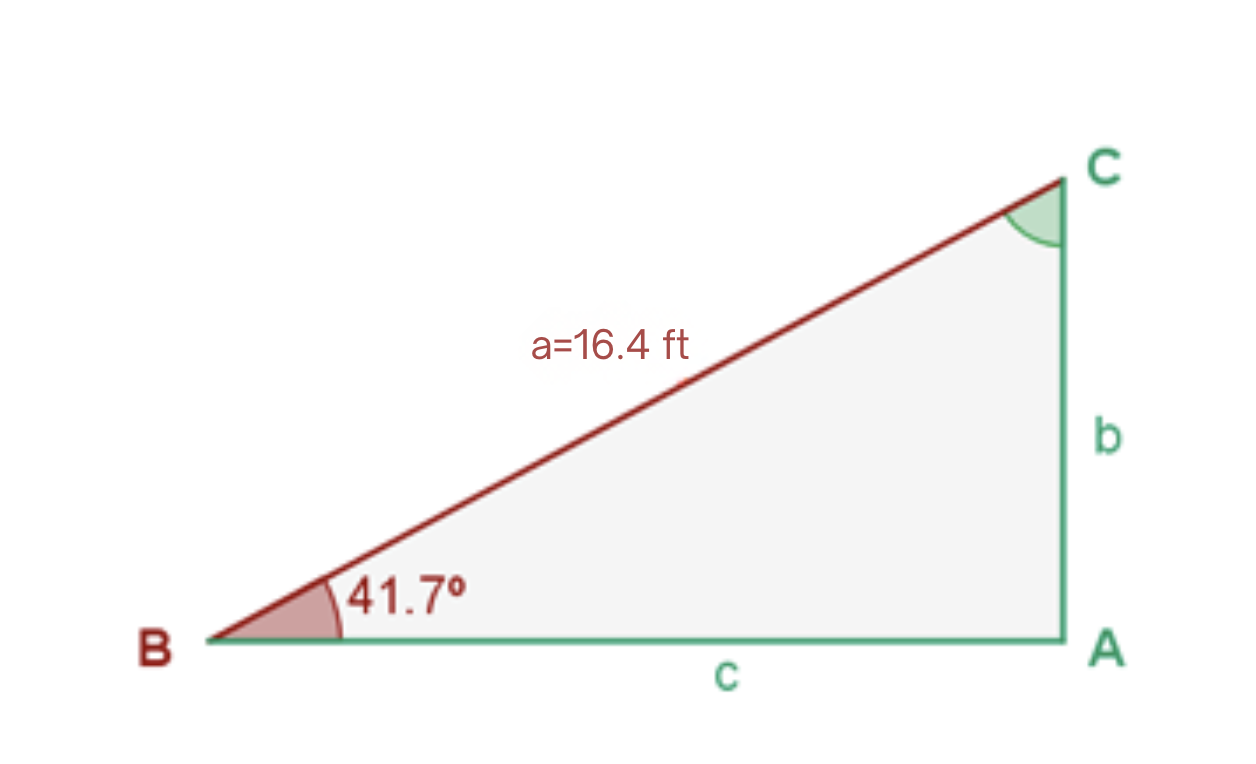
Since we already know two of the three angles, we can calculate the missing one,  , directly:
, directly:
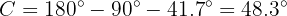
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
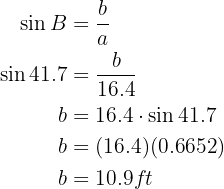
To obtain side  we will apply cosine to angle
we will apply cosine to angle  and solve for
and solve for  :
:
We have found the missing sides and angles.
In a right triangle  , a leg and an angle are known:
, a leg and an angle are known: 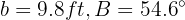 . Solve the triangle.
. Solve the triangle.
Let's obtain the missing sides and angles. Note that since it is a right triangle, we already know angle 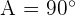 .
.
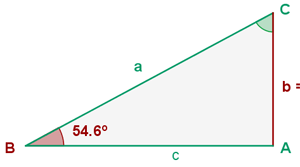
Since we already know two of the three angles, we can calculate the missing one,  , directly:
, directly:
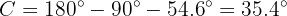
To obtain side  we will apply tangent to angle
we will apply tangent to angle  and solve for
and solve for  :
:
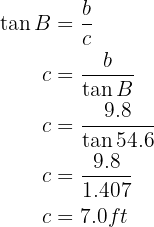
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
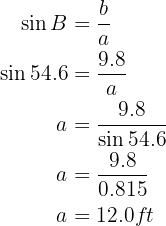
We have found the missing sides and angles.
In a right triangle  , the hypotenuse and a leg are known:
, the hypotenuse and a leg are known: 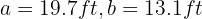 . Solve the triangle.
. Solve the triangle.
Let's obtain the missing sides and angles. Note that since it is a right triangle, we already know angle 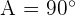 .
.
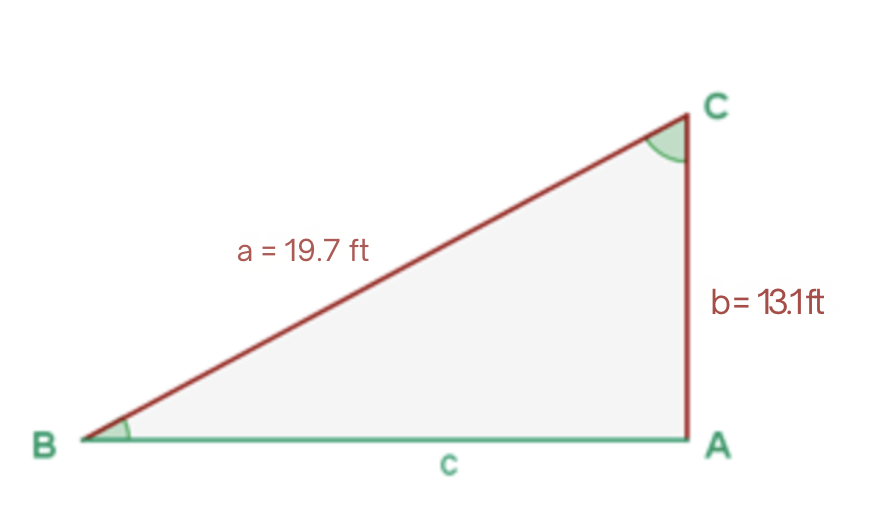
To obtain angle  we will first calculate the cosine of the angle using the leg and hypotenuse we know, then apply the inverse function arccosine:
we will first calculate the cosine of the angle using the leg and hypotenuse we know, then apply the inverse function arccosine:
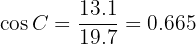
Applying arccosine we obtain 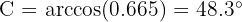 . Note that now that we have two of the three angles, we can directly calculate the missing angle:
. Note that now that we have two of the three angles, we can directly calculate the missing angle:
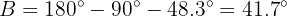
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
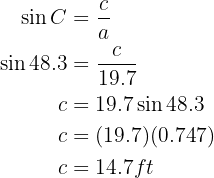
We have found the missing sides and angles.
In a right triangle  , the two legs are known:
, the two legs are known: 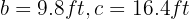 . Solve the triangle.
. Solve the triangle.
Let's obtain the missing sides and angles. Note that since it is a right triangle, we already know angle 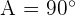 .
.
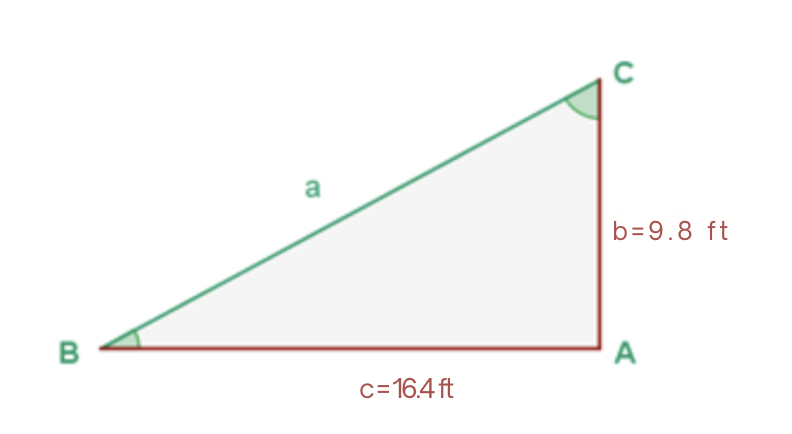
To obtain angle  we will first calculate its tangent using the legs and then calculate the arctangent:
we will first calculate its tangent using the legs and then calculate the arctangent:
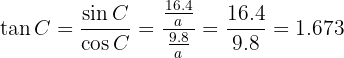
Thus, we have 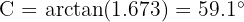 . Now that we have two of the three angles, we can obtain the missing one directly:
. Now that we have two of the three angles, we can obtain the missing one directly:
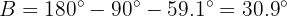
To obtain side  we will apply sine to angle
we will apply sine to angle  and solve for
and solve for  :
:
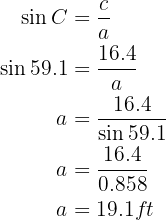
We have found the missing sides and angles.
In a right triangle  , we have the following information: the hypotenuse is
, we have the following information: the hypotenuse is 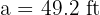 and
and 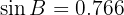 . Solve the triangle.
. Solve the triangle.
Note that since it is a right triangle, we know that angle 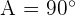 .
.

Applying arcsine we have:
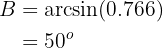
Now, once we have two angles, we can immediately calculate the last one:
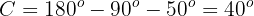
Applying cosine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
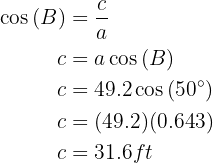
Applying sine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
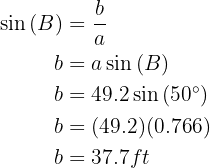
Thus we have obtained the missing data.
In a right triangle  , we have the following information: the hypotenuse is
, we have the following information: the hypotenuse is 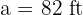 and
and 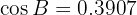 . Solve the triangle.
. Solve the triangle.
Note that since it is a right triangle, we know that angle 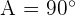 .
.

Applying arccosine we have:
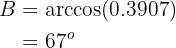
Now, once we have two angles, we can immediately calculate the last one:
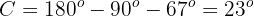
Applying cosine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
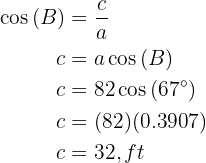
Applying sine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
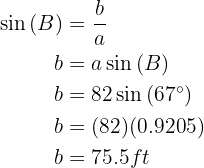
Thus we have obtained the missing data.
In a right triangle  , we have the following information: the hypotenuse is
, we have the following information: the hypotenuse is 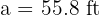 and
and 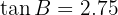 . Solve the triangle.
. Solve the triangle.
Note that since it is a right triangle, we know that angle 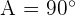 .
.

Applying arctangent we have:
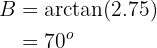
Now, once we have two angles, we can immediately calculate the last one:
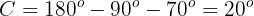
Applying cosine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
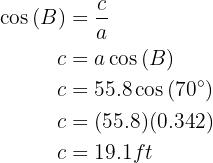
Applying sine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
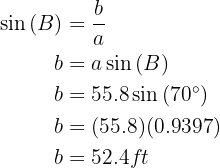
Thus we have obtained the missing data.
In a right triangle  , we have the following information: the hypotenuse is
, we have the following information: the hypotenuse is 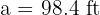 and
and 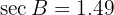 . Solve the triangle.
. Solve the triangle.
Note that since it is a right triangle, we know that angle 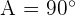 .
.

Applying arcsecant we have:
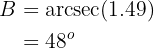
Now, once we have two angles, we can immediately calculate the last one:
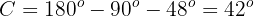
Applying cosine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
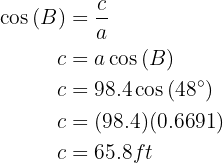
Applying sine to angle  and solving, we will obtain the value of side
and solving, we will obtain the value of side  :
:
Thus we have obtained the missing data.
A tree 164 feet tall casts a shadow 197 feet long. Find the angle of elevation of the sun at that moment.
Observe that a 90° angle is formed between the ground and the tree. Thus, we have two legs. Additionally, we have that the angle of elevation is the angle formed at the vertex where the shadow ends, as seen in the following image.
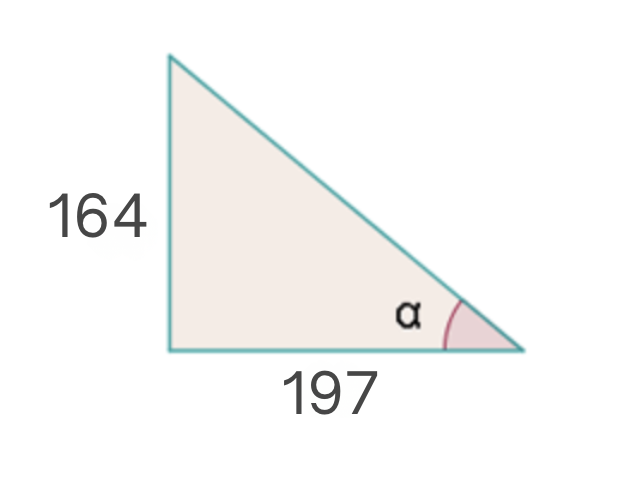
Therefore, to obtain our angle of elevation  , we will first calculate its tangent using the legs and then apply arctangent to our result:
, we will first calculate its tangent using the legs and then apply arctangent to our result:
Therefore, we have  .
.
A blimp flying at 2,625 feet altitude spots a town with a depression angle of 12°. How far from the town is it?
We have that the data provided gives us the scheme shown in the following image.
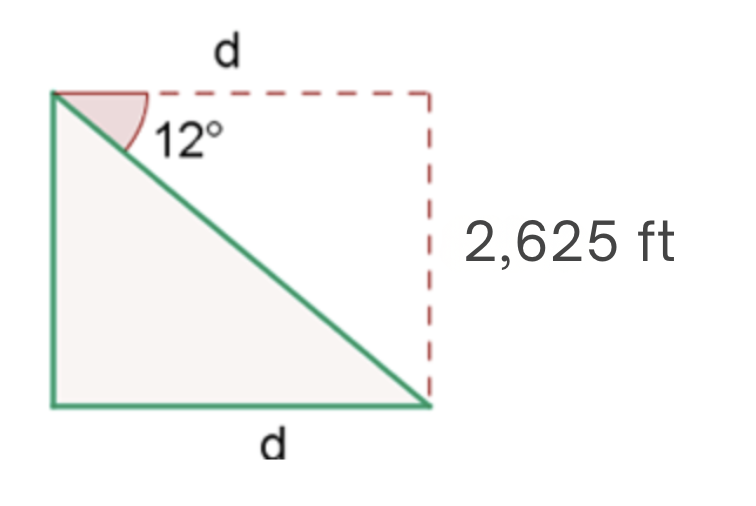
Note that what we really want is to find the distance the blimp must travel to be flying over the town. That is, we want to find leg  . To do this, we will calculate the tangent of the angle with value 12° and at the same time use the legs and from there solve for
. To do this, we will calculate the tangent of the angle with value 12° and at the same time use the legs and from there solve for  :
:
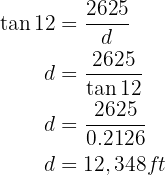
Find the radius of a circle knowing that a chord of 80.7 feet has a corresponding arc of 70°.
Remember that the central angle measures the same as the arc it spans. Having said that, we have the following scheme.
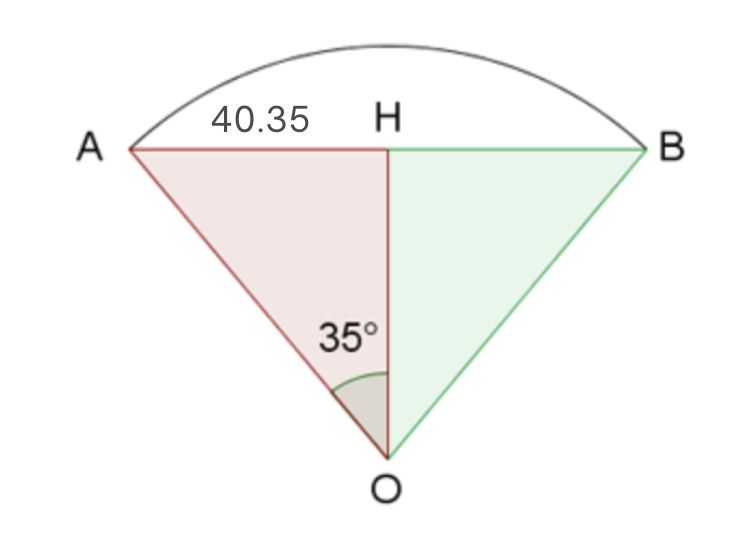
To obtain the radius (side  ), we will apply sine to the angle measuring 35° using the leg we know and
), we will apply sine to the angle measuring 35° using the leg we know and  , then solve for the radius:
, then solve for the radius:

Calculate the area of a triangular plot, knowing that two of its sides measure 262.5 feet and 426.5 feet, and they form an angle of 70° between them.
We have that angle 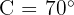 . Now, the following image shows the triangle.
. Now, the following image shows the triangle.
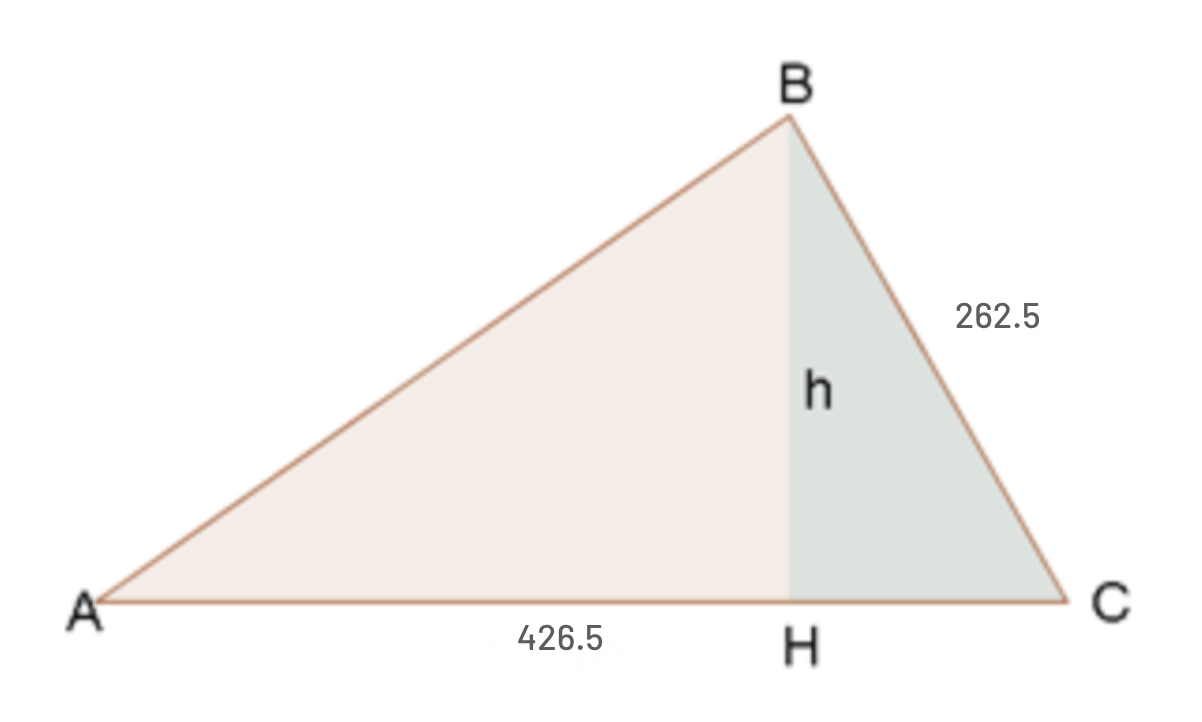
Note that the height divides our initial triangle into two right triangles. We will use the triangle on the right, since we have more information about it, to obtain the height value and then calculate the area. To obtain the height, we will use the sine of angle  , the leg that belongs to this triangle, and the height, thus we will end up solving for the height:
, the leg that belongs to this triangle, and the height, thus we will end up solving for the height:
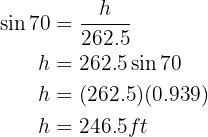
Now that we know the height measures 246.5 feet, we will calculate the area:
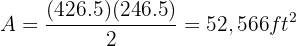
Calculate the height of a tree, knowing that from a point on the ground its top is observed at an angle of 30° and if we approach 32.8 feet, at an angle of 60°.
First let's try to illustrate the problem to better understand it. The following image will help us with that.
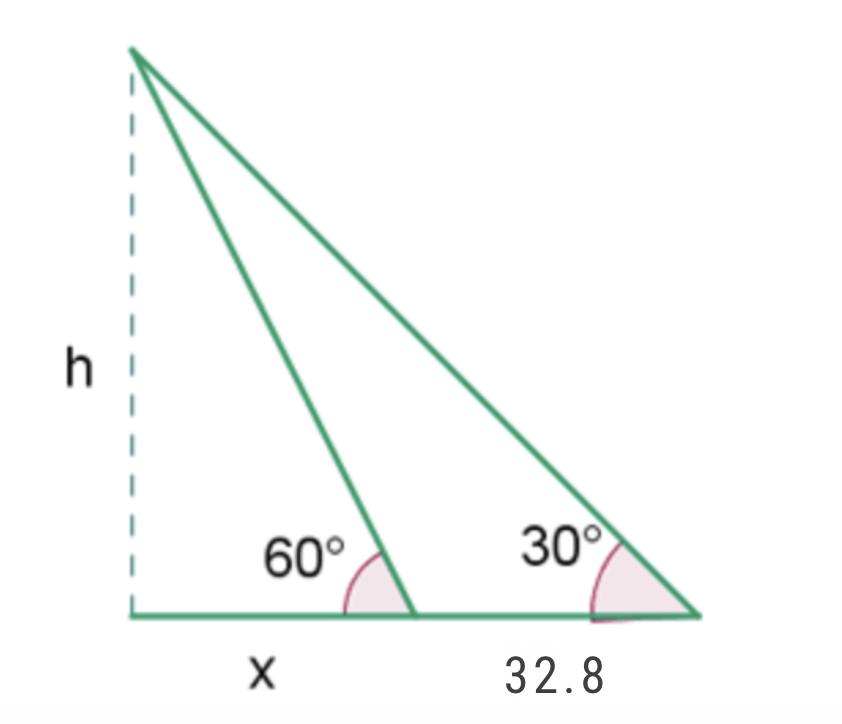
To solve the problem, we will first calculate the tangent of the 30° angle and its corresponding legs, and then we will calculate the tangent of the 60° angle with its corresponding legs and solve for  from both:
from both:
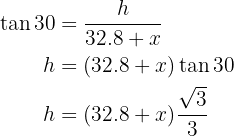
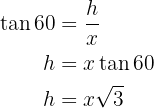
Note that this will give us a system of equations that we will solve for the height:
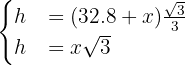
Solving the system we have 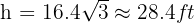 .
.
The length of the side of a regular octagon is 39.4 feet. Find the radii of the inscribed and circumscribed circles.
The following image allows us to observe which is the radius of the inscribed circle and which is the circumscribed circle.
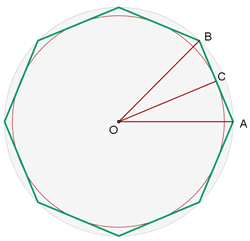
Note that side 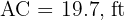 . Additionally, side defines the radius of the inscribed circle, while side
. Additionally, side defines the radius of the inscribed circle, while side 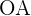 defines the radius of the circumscribed circle. Also, we know that angle
defines the radius of the circumscribed circle. Also, we know that angle 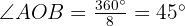 since it is an octagon, therefore, we have
since it is an octagon, therefore, we have 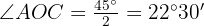 .
.
Radius of the inscribed circle
We will calculate the tangent of angle 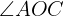 using both the angle value and the legs to, at the end, be able to solve for leg :
using both the angle value and the legs to, at the end, be able to solve for leg :
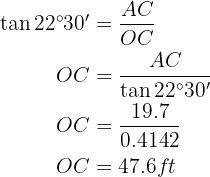
Radius of the circumscribed circle
We will calculate the sine of angle 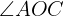 using both the angle value and the leg and hypotenuse to, at the end, be able to solve for hypotenuse
using both the angle value and the leg and hypotenuse to, at the end, be able to solve for hypotenuse 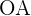 :
:
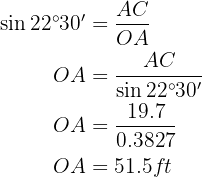
Calculate the length of the side and apothem of a regular octagon inscribed in a circle with a radius of 19.3 inches.
The following image allows us to better observe the problem.
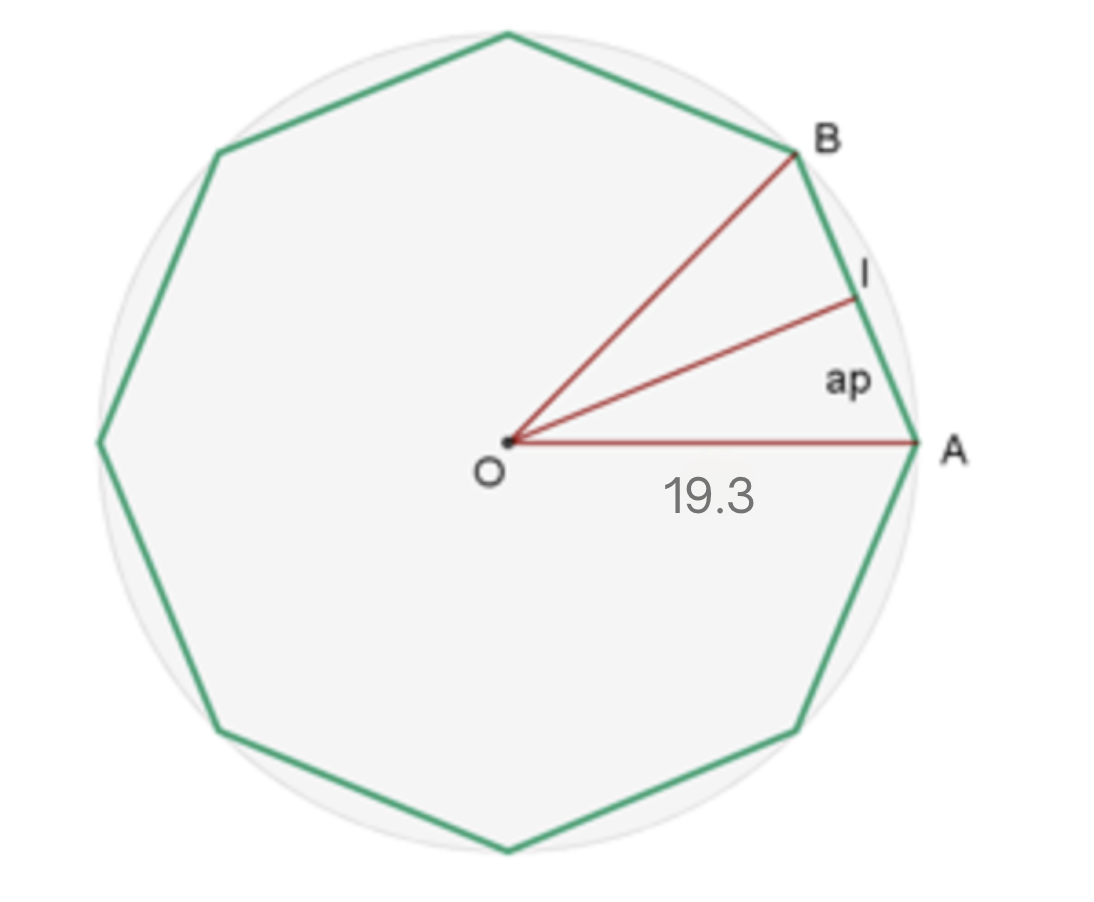
Note that the radius equals side 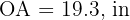 . Now, the side of the octagon is defined by
. Now, the side of the octagon is defined by  and
and 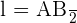 .
.
Also note that the apothem 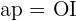 divides angle
divides angle 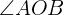 in two. Additionally, we know that angle
in two. Additionally, we know that angle 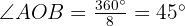 since it is an octagon, therefore, we have
since it is an octagon, therefore, we have 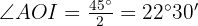 . Also observe that sides
. Also observe that sides 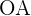 ,
,  , and
, and 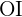 form a right triangle.
form a right triangle.
Side of the octagon
We will calculate the sine of angle 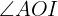 using both the angle value and the hypotenuse (the radius of the octagon) and the leg (half the side of the octagon) to, at the end, be able to solve for leg
using both the angle value and the hypotenuse (the radius of the octagon) and the leg (half the side of the octagon) to, at the end, be able to solve for leg  :
:
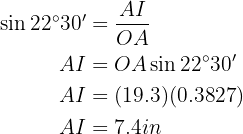
Therefore, the side measures 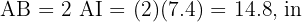 .
.
Apothem of the octagon
We will calculate the cosine of angle 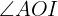 using both the angle value and the hypotenuse (the radius of the octagon) and the leg (the apothem) to, at the end, be able to solve for leg
using both the angle value and the hypotenuse (the radius of the octagon) and the leg (the apothem) to, at the end, be able to solve for leg 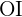 :
:
Three towns  ,
,  , and
, and  are connected by roads. The distance from
are connected by roads. The distance from  to
to  is 3.73 miles and from
is 3.73 miles and from  to
to  is 5.59 miles. Additionally, the angle formed by these roads is 120°. How far apart are
is 5.59 miles. Additionally, the angle formed by these roads is 120°. How far apart are  and
and  ?
?
The following image allows us to better observe the problem.
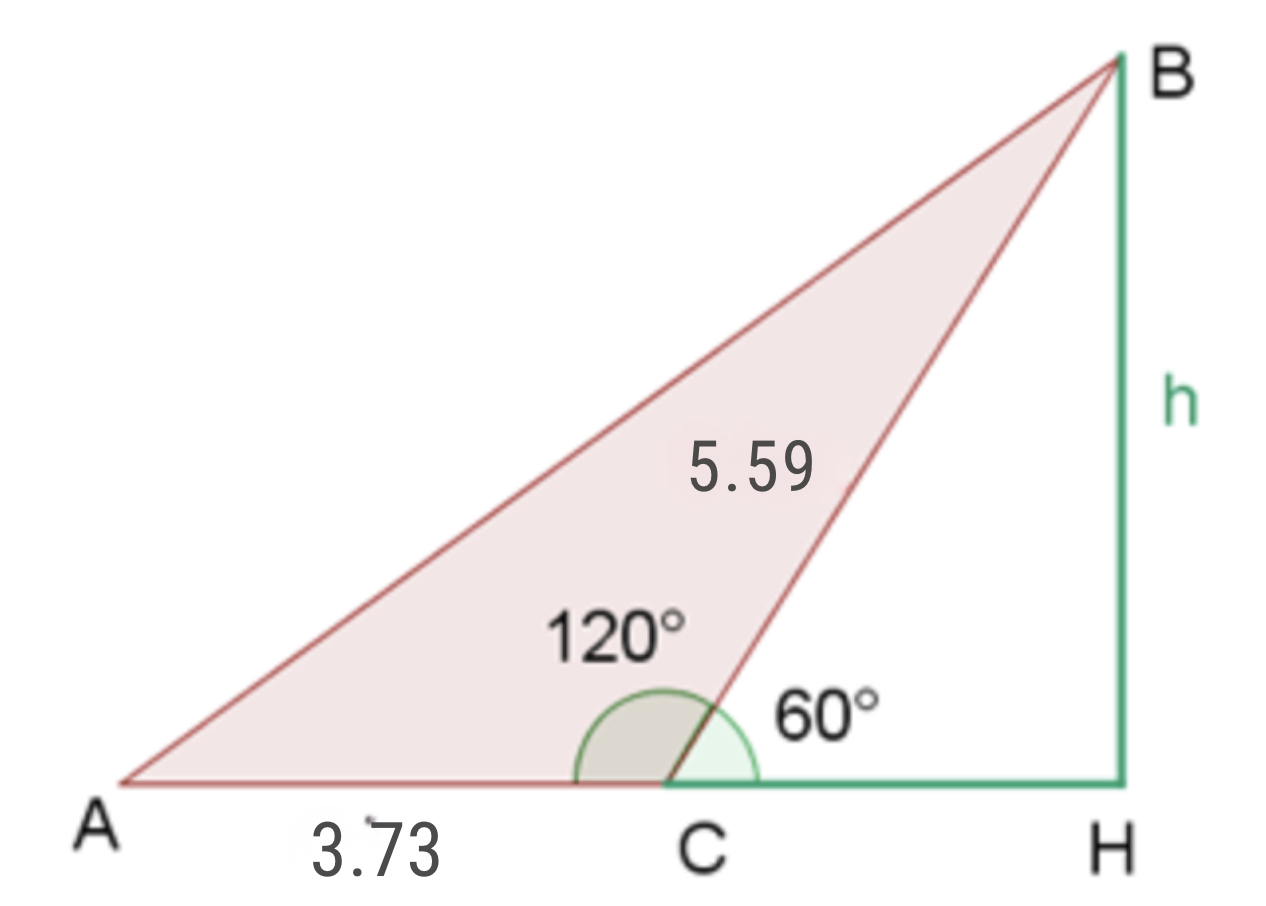
Note that we have made some additional constructions to be able to solve the problem using right triangles. To solve the problem, we must first find the legs of the right triangle we have formed (the green one) and thus, later, we will use this data to obtain the legs of the larger triangle and, therefore, the hypotenuse, which is the value we are looking for.
Legs of the green right triangle
We will calculate the sine and cosine of angle 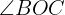 using both the angle value and the legs and hypotenuse to, at the end, be able to solve for legs
using both the angle value and the legs and hypotenuse to, at the end, be able to solve for legs  and
and  , respectively:
, respectively:


Legs of the larger right triangle and hypotenuse
We will use the Pythagorean theorem to calculate the hypotenuse. First, note that the legs we will use will be  and
and 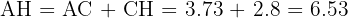 :
:
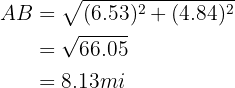
Summarize with AI:


