Paolo Ruffini (1765-1822) was an Italian mathematician who established a shorter method for dividing polynomials when the divisor is a binomial of the form x - a.
Ruffini's Rule
To explain the steps to apply in Ruffini's rule, we will take two examples:
First Example of Ruffini's Rule
Divide:
1. If the polynomial is not complete, we complete it by adding the missing terms with zeros.
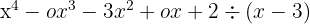
2. We place the coefficients of the dividend in a line.
3. Below on the left, we place the opposite of the independent term of the divisor: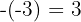 
.
4. We draw a line and bring down the first coefficient 
.
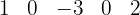
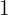
5. We multiply that coefficient by the divisor 
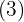and place it below the next term 
.
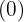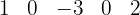
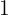
6. We add the two coefficients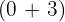 
.
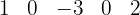
7. We repeat the previous process: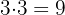 
and 
.
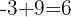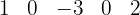
We repeat the process again: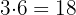 
and 
.
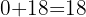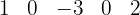
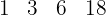
We repeat again: 
and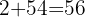 
.
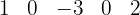
8. The last number obtained,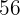 
, is the remainder.
9. The quotient is a polynomial of degree one unit less than the dividend, and whose coefficients are those we have obtained.
Quotient: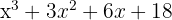
Remainder: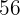
Second Example of Ruffini's Rule
Divide using Ruffini's rule: 
1. If the polynomial is not complete, we complete it by adding the missing terms with zeros.
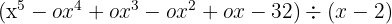
2. We place the coefficients of the dividend in a line.
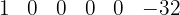
3. Below on the left, we place the opposite of the independent term of the divisor: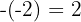 
.
4. We draw a line and bring down the first coefficient .
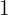
5. We multiply that coefficient by the divisor 
and place it below the next term .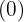
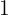
6. We add the two coefficients 
.
7. We repeat steps 
and 
until the end.
8. The quotient is a polynomial of degree one unit less than the dividend, and whose coefficients are those we have obtained.
Quotient:
Remainder:
Summarize with AI:
Did you like this article? Rate it!
Loading...
