Welcome to our page dedicated to exercises and solved word problems using the rule of three! The rule of three is one of the most practical and useful tools in mathematics when it comes to finding proportions between different quantities. Think of it as a compass that helps us navigate situations where we need to relate values and find precise ratios.
In this space, we’ll break down various problems and exercises so you can sharpen your skills in the art of proportionality. Whether you're looking to improve your everyday math abilities or apply the rule of three to more complex scenarios — you're in the right place. Get ready to challenge your mind and become a rule of three pro!
Looking for a math tutor? Why not find one on Superprof? The first lesson is free!
Two wheels are connected by a transmission belt. The first has a radius of  inches and the second
inches and the second  inches. When the first has made
inches. When the first has made  turns, how many turns will the second have made?
turns, how many turns will the second have made?
First let's note that these are inversely proportional quantities, since the larger the radius, the fewer turns it will make. If  represents the value of turns we're looking for, from the following diagram we obtain that
represents the value of turns we're looking for, from the following diagram we obtain that
The portion of turns equals the portion of radius in the following sense
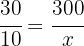
Therefore the value of  is
is
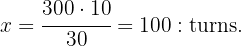
The scale on a map is as follows:  inches on the map represents
inches on the map represents 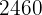 feet in reality. How many feet in reality do
feet in reality. How many feet in reality do 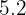 inches on the map equal?
inches on the map equal?
First let's note that these quantities are directly proportional, that is, the more inches on the map, the more feet in real life there will be. Thus, if  represents the number of feet in reality, then from the following diagram we obtain that
represents the number of feet in reality, then from the following diagram we obtain that
The proportion of feet equals the proportion of inches in the following sense
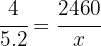
Therefore the value of  is
is
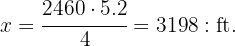
Six people can stay in a hotel for  days for $
days for $ 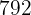 . How much will the hotel cost for
. How much will the hotel cost for  people for eight days?
people for eight days?
More people means higher cost and more days means higher cost as well, therefore they are directly proportional quantities. Let  be the cost value we are looking for, then
be the cost value we are looking for, then
Therefore the portion of people multiplied by the portion of days equals the portion of money, that is,
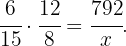
Now we solve for the value of 
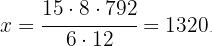
Thus the hotel for  people for eight days will cost $
people for eight days will cost $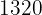 .
.
A convenience store charges 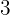 for every
for every 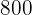 sent, and if the amount is not exact, the corresponding amount is charged. If a person deposited
sent, and if the amount is not exact, the corresponding amount is charged. If a person deposited 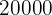 , how much did the convenience store charge for the transfer?
, how much did the convenience store charge for the transfer?
First let's note that these are directly proportional quantities, since the more money sent, the higher the charge. Thus, if  represents the amount charged for sending the money, from the following diagram we obtain that
represents the amount charged for sending the money, from the following diagram we obtain that
The proportion of money charged equals the proportion of money sent in the following sense
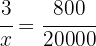
Therefore the value of  is
is
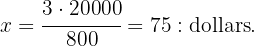
If with  cans of
cans of  gallon of paint each,
gallon of paint each, 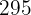 feet of fence
feet of fence  inches high have been painted. Calculate how many
inches high have been painted. Calculate how many  gallon cans of paint will be needed to paint a similar fence
gallon cans of paint will be needed to paint a similar fence  inches high and
inches high and  feet long.
feet long.
The more paint a can contains, the fewer cans we will need. They are inversely proportional quantities. The more surface we have to paint, the more cans we will need. They are directly proportional quantities. This information allows us to set up the following diagram
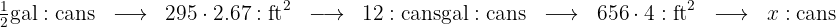
In this case we have that  represents the number of paint cans we need. In the middle column of the diagram we have converted the fence height to feet and calculated the area of said fence by multiplying height by length.
represents the number of paint cans we need. In the middle column of the diagram we have converted the fence height to feet and calculated the area of said fence by multiplying height by length.
Now we solve for the value of  from the following equation
from the following equation
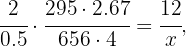
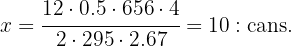
If a house takes  days to build with
days to build with  workers working. How many days will it take if
workers working. How many days will it take if  additional workers are hired?
additional workers are hired?
First let's note that the workers variable is inverse to the days variable, since it is reasonable that with more workers working, they will take less time building the house. Thus, if  represents the value of days we're looking for, from the following diagram we obtain that
represents the value of days we're looking for, from the following diagram we obtain that
The proportion of workers is inverse to the number of days in the following sense
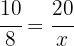
Therefore the value of  is
is
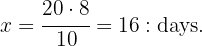
 workers plow a rectangular field
workers plow a rectangular field 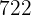 feet long and
feet long and  feet wide in
feet wide in  days. How many workers will be needed to plow another similar field
days. How many workers will be needed to plow another similar field 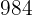 feet long by
feet long by  feet wide in five days?
feet wide in five days?
More surface means more days needed. They are directly proportional quantities. More days means fewer workers needed. They are inversely proportional quantities. Thus we have the following diagram
In setting up the diagram, in the first column we have calculated the area of the field by multiplying width by length. Now we must solve for the value of  from the following equation
from the following equation
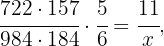
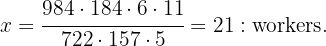
This means we need  workers to plow the field
workers to plow the field 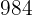 feet long by
feet long by  feet wide in five days.
feet wide in five days.
 nurses are required to care for
nurses are required to care for  patients in
patients in  days. How many nurses are needed to care for
days. How many nurses are needed to care for 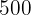 patients in
patients in  days?
days?
First let's note that with more nurses, fewer days will be needed to care for the patients, so the days variable is inverse. Similarly, with more patients, more nurses will be required, so the patients variable is direct. Therefore, let  be the number of nurses we are looking for, then we can represent the problem as follows:
be the number of nurses we are looking for, then we can represent the problem as follows:
Therefore, the inverse proportion of days multiplied by the proportion of patients equals the proportion of nurses since the days variable is inverse and the patients variable is direct, that is, 
Now we solve for the value of 
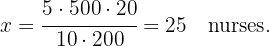
Six faucets take  hours to fill a tank with
hours to fill a tank with 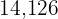 cubic feet capacity. How many hours will four faucets take to fill
cubic feet capacity. How many hours will four faucets take to fill  tanks of
tanks of 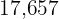 cubic feet each?
cubic feet each?
More faucets means fewer hours. They are inversely proportional quantities. More tanks means more hours. They are directly proportional quantities. More cubic feet means more hours. They are directly proportional quantities. With this information we can set up the following diagram
These  quantities in proportion are related as follows
quantities in proportion are related as follows
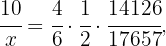
solving for the value  of hours we have that
of hours we have that
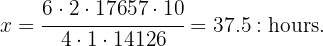
We conclude that four faucets take  hours to fill
hours to fill  tanks of
tanks of 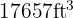 .
.
 sewing machines made
sewing machines made  garments yesterday. If only
garments yesterday. If only  machines will be available today, how many garments will they make today?
machines will be available today, how many garments will they make today?
Let's note that the machines variable is a direct variable, that is, having fewer machines means fewer garments will be made. Thus, if  represents the number of garments we're looking for, from the following diagram we obtain that
represents the number of garments we're looking for, from the following diagram we obtain that
Therefore, the proportion of machines equals the proportion of garments in the following sense
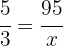
Therefore the value of  is
is
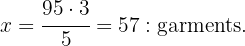
Summarize with AI:


