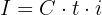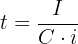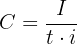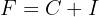At some banks, in savings accounts, loans, or pawn agreements, you may notice that a monthly interest is charged. However, not all interest is calculated this way.
The period refers to the time over which interest is applied. This can be annually, monthly, weekly, or even daily.
For the purposes of the exercises in this section, we’ll be working with annual interest.
Also, keep in mind there are two types of interest: simple interest and compound interest. The exercises here will focus on simple interest.
Formulas to Calculate Interest
The following symbols will be used:
: Interest
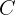: Initial capital (principal)
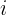: Interest rate
: Time
: Final capital (or future value)
So, the formulas for calculating simple interest, when the interest rate and time are expressed in the same unit, are:
⚠️ Note: If time and interest rate use different units, you must convert them before using the formulas.
Practice Exercises on Interest Calculation
How long should $25,000 be invested at 5% annual interest to grow to $30,000?
We’re given the initial capital and the final amount. So first, we calculate the interest earned:
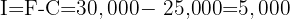
Now we can use the formula for time:
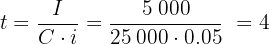
Answer: The money must be invested for 4 years.
$200 is invested, and after 2 years the total amount grows to $250. What was the interest rate?
We’re given the initial and final amounts. First, calculate the interest earned:
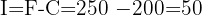
Now apply the formula for the interest rate:
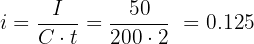
Convert to a percentage:
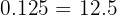
Answer: The interest rate was 12.5% per year.
What amount must be invested to earn $1,500 in 3 years at 20% annual interest?
We’re given the final amount, the interest rate, and the time. First, express the interest in terms of the capital:
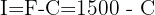
Now use the interest formula to solve for :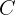
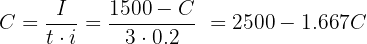
Solve for initial capital:
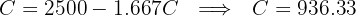
Answer: The required capital is approximately $937.
A loan of $45,000 is repaid with $52,500 after 1 year, 4 months, and 15 days. What is the annual interest rate?
Step 1: Convert the time to days
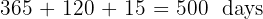
Step 2: Calculate the interest earned
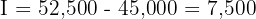
Step 3: Use the interest formula to find the daily rate
Step 4: Convert daily interest rate to annual percentage rate
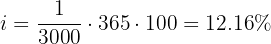
Answer: The annual interest rate is 12.16%.
A loan of $5,000 is repaid with $5,500 after 10 months and 15 days. What is the monthly interest rate?
Step 1: Convert time to days
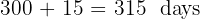
Step 2: Calculate the interest
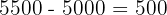
Step 3: Use the formula to find the daily interest rate
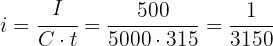
Step 4: Convert to monthly rate and percentage
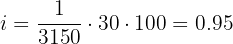
Answer: The monthly interest rate is 0.95%.
Peter invests $15,000 and receives $20,000 after 14 months. What is the bimonthly interest rate?
Step 1: Convert time to bimesters
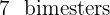
Step 2: Calculate the interest earned
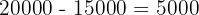
Step 3: Use the formula
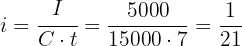
Step 4: Convert to percentage
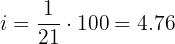
Answer: The bimonthly interest rate is 4.76%.
Mary invests $7,238 and receives $10,050 after 1 year, 2 months, and 5 days. What is the semiannual interest rate?
Step 1: Convert the time to days
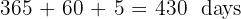
Step 2: Calculate the interest earned
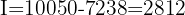
Step 3: Use the formula to calculate the daily rate
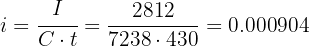
Step 4: Convert daily rate to semiannual percentage rate
Multiply by 365 to get annual, then by 0.5 for semiannual, then by 100:
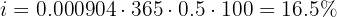
Answer: The semiannual interest rate is 16.5%.
At what simple interest rate should money be loaned so that after t years the interest equals k times the capital?
We want the interest to be equal to a multiple of the capital:
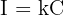
Substitute into the formula:
Cancel out 
on both sides (as it's not zero):
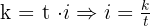
Answer: The interest rate is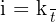 
At what annual interest rate should money be loaned so that in 20 years the interest equals the capital?
We want:
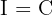
Substitute into the formula:
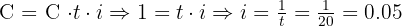
Convert to percentage:
Answer: The interest rate is 5% annually.
How long should $30,000 be invested at a 0.45% monthly rate to earn $5,000 in interest?
We start by finding how many times the interest fits into the capital:
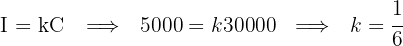
Use the formula from Exercise 8:
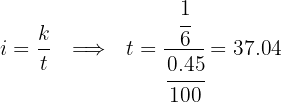
Answer: The time required is 37.04 months, or 3 years, 1 month, and 12 days.
How long will it take for the interest to equal three times the initial capital at 6% interest?
We want:
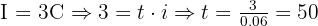
Answer: The interest will triple the capital in 50 years.
(You could also use Exercise 8’s formula with 
and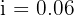 
)
What is the interest earned over 5 years on a capital of $30,000 at 6%?
We just need to find 
. Use the formula:
Answer: The interest is $9,000.
What capital is required to earn $500 in interest at 3.5% over 1.5 years?
We’re solving for . Use the formula:
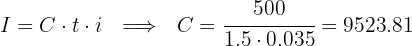
Answer: The required capital is $9,523.81.
What will be the final amount after 6 months if $10,000 is invested at a 3.5% annual rate?
Step 1: Convert months to years
.
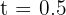Step 2: Calculate interest
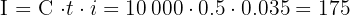
Step 3: Add to original capital
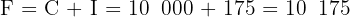
Answer: The final capital is $10,175 after 6 months.
John invests $635 at 4.68% annually. What will his capital be after 8 months?
To solve this exercise, we first need to calculate the interest earned over 8 months. Since the interest rate is annual, we convert it to a monthly rate:
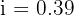
Now we calculate the interest:
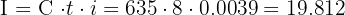
Once we have the interest, we can calculate the final capital using:
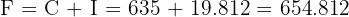
Answer: The final capital is $654.81 after 8 months.
Did you like this article? Rate it!
Loading...
