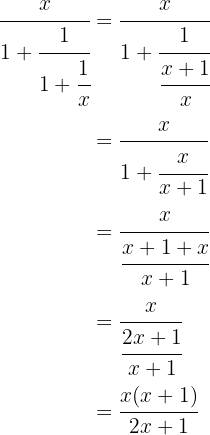In these exercises we will cover the topics:
- Simplification of algebraic fractions
- Addition of algebraic fractions
- Subtraction of algebraic fractions
- Multiplication of algebraic fractions
- Division of algebraic fractions
- Operations with algebraic fractions
Simplify the following algebraic fractions:
a 
b 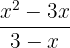
c 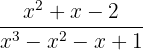
d 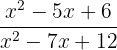
e 
f 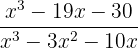
a 
We extract the common factor  from the numerator and denominator expressions, thus we have
from the numerator and denominator expressions, thus we have
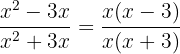
Now, we "cancel said common factor", thus our simplification becomes
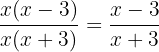
b 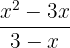
We extract the common factor  from the numerator
from the numerator
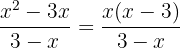
We multiply numerator and denominator by  , so we will obtain an equivalent fraction
, so we will obtain an equivalent fraction
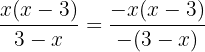
Distributing the sign in the denominator we have

Canceling the common factor in the denominator and numerator we obtain
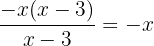
c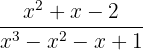
We apply the remainder theorem:


We divide by Ruffini both the numerator and denominator expressions
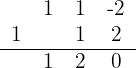
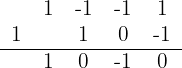
We have an exact division, thus  and therefore
and therefore
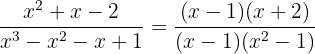
We simplify by canceling the common factor from the numerator and denominator
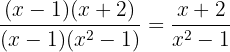
Note that the denominator  , however, neither of these factors is in the numerator, so it cannot be canceled or simplified further in that sense, but we can write the expression as
, however, neither of these factors is in the numerator, so it cannot be canceled or simplified further in that sense, but we can write the expression as
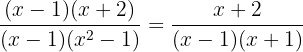
Either of the two expressions in the equality are correct and valid.
d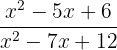
Using the quadratic formula we obtain the roots of the numerator polynomial and the denominator polynomial, this will help us express said polynomials as multiplication of binomials defined by their roots
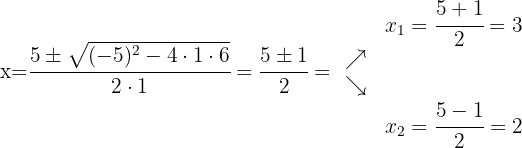
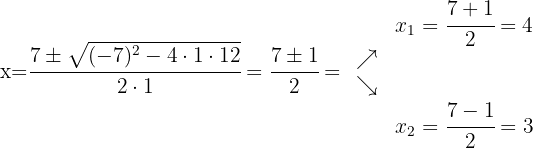
We factor: 
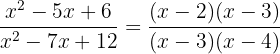
We simplify
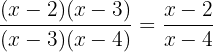
e
Using the quadratic formula we obtain the roots of the numerator polynomial and the denominator polynomial, this will help us express said polynomials as multiplication of binomials defined by their roots
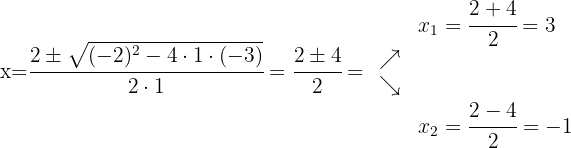
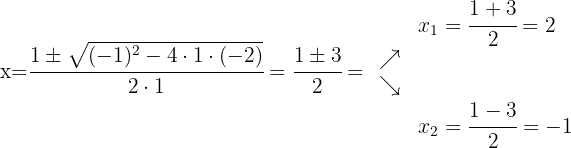
We factor: 

We simplify

f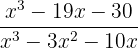
In the numerator we use the remainder theorem and Ruffini's rule to find the integer roots
The divisors of  are: {
are: { }
}

We divide by Ruffini
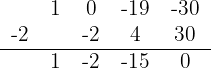
The numerator satisfies

We can continue factoring the trinomial in the same way or using the quadratic formula
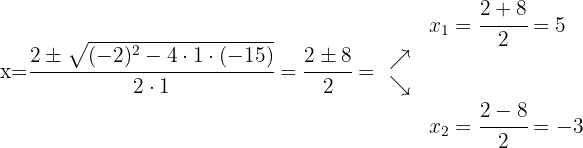

In the denominator we extract the common factor 

To factor the trinomial we use the general formula

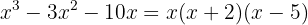
Thus, our initial expression can be written as
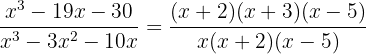
We simplify

Perform the following addition of algebraic fractions

We need to find the common denominator, for this we have to find the LCM of the denominators, note that

We divide the common denominator by the denominators of the given fractions and multiply the result by the corresponding numerator

Perform the following addition of algebraic fractions

We need to find the common denominator, for this we have to find the LCM of the denominators, note that

We divide the common denominator by the denominators of the given fractions and multiply the result by the corresponding numerator

Perform the following addition of algebraic fractions

We need to find the common denominator, for this we have to find the LCM of the denominators, note that

We divide the common denominator by the denominators of the given fractions and multiply the result by the corresponding numerator

Perform the following addition of algebraic fractions
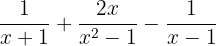
We need to find the common denominator, for this we have to find the LCM of the denominators, note that
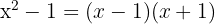
Thus

We divide the common denominator by the denominators of the given fractions and multiply the result by the corresponding numerator

We extract the common factor 

We simplify
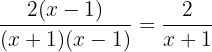
Perform the following subtraction of algebraic fractions

We need to find a common denominator, for this we have to find the LCM of the denominators. Note that

Thus

We divide the common denominator by the denominators of the given fractions and multiply the result by the corresponding numerator and operate

Furthermore, we have that  , thus we obtain
, thus we obtain
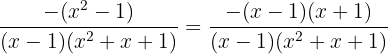
We simplify

Perform the product of algebraic fractions

We have a sum times difference which we express as a difference of squares, therefore

We find a common denominator

We operate

Perform the product of algebraic fractions

We have a sum times difference which we express as a difference of squares, therefore

We find a common denominator

We extract the common factor  and operate
and operate

We multiply
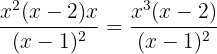
Perform the quotient of algebraic fractions

The division of two algebraic fractions is another algebraic fraction whose numerator is the product of the numerator of the first times the denominator of the second, and as denominator the product of the denominator of the first times the numerator of the second.
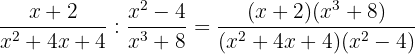
The second binomial is a sum of cubes: 
The trinomial in the denominator is a perfect square trinomial and the binomial is a difference of squares that factors as a sum times difference.

We simplify
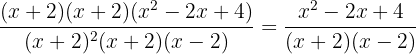
or

Perform the quotient of algebraic fractions

By dividing we have
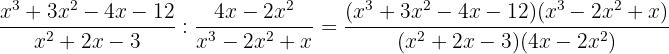
The first factor decomposes using the remainder theorem and division by Ruffini.
In the second factor we extract the common factor  , we are left with a perfect square trinomial which we express as a binomial squared.
, we are left with a perfect square trinomial which we express as a binomial squared.
The first factor of the denominator is a second-degree trinomial that factors using the general formula. In the second factor we extract the common factor  . Thus, our original expression would be
. Thus, our original expression would be
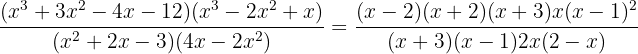
simplifying a bit
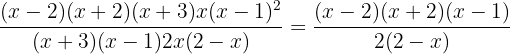
We multiply the numerator and denominator by  , obtaining an equivalent fraction.
, obtaining an equivalent fraction.
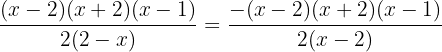
We simplify
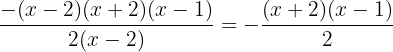
Perform the quotient of algebraic fractions

The division of two algebraic fractions is another algebraic fraction whose numerator is the product of the numerator of the first times the denominator of the second, and as denominator the product of the denominator of the first times the numerator of the second.

The second binomial in the denominator is a difference of cubes: 
The first trinomial in the numerator is a perfect square trinomial.

We simplify

Perform the ratio of algebraic fractions

We find a common denominator

The division of two algebraic fractions is another algebraic fraction whose numerator is the product of the numerator of the first times the denominator of the second, and as denominator the product of the denominator of the first times the numerator of the second.

We simplify

Perform the ratio of algebraic fractions

We find a common denominator

The division of two algebraic fractions is another algebraic fraction whose numerator is the product of the numerator of the first times the denominator of the second, and as denominator the product of the denominator of the first times the numerator of the second.

We simplify

Simplify the following algebraic fraction

First we subtract  and then we take the inverse of the result.
and then we take the inverse of the result.

Simplify the following algebraic fraction

First we add 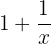 and take the inverse of the result, then we add again and so on until we find our result.
and take the inverse of the result, then we add again and so on until we find our result.