Chapters
Substitution Method for Systems of Equations
The substitution method, as its name suggests, consists of isolating the value of a variable obtained from one of the equations and substituting it into another equation.
Note
When a system has more unknowns (variables) than the number of equations, then the system has infinite solutions, that is, each variable can take different values, such that they always satisfy the equation, the number of values that each variable can take is infinite.
Example:
Given the equation: 
We observe that it is an equation with two variables. We can quickly realize some of the values that are solutions:
Let's note that there is an infinite number of values that we can assign to 
and 
for them to be a solution.
On the other hand, when the system has the same number of equations and unknowns, then generally the system has a unique solution.
Example of the Method with a 2x2 System
We will call 
"Equation I" and 
is "Equation II"
We isolate either of the 2 variables in one of the 2 equations, (we should always look for the one that requires less algebraic work for our convenience), in this case, we will isolate in Equation I
This is called "Value of with respect to "
We substitute the isolated value into the other equation, in this case, we substitute the value of into Equation II
As we can notice, now in the equation there is only the variable . This equation can be simplified and solved to obtain the value of .
Once we have the value of one of the variables, in this case , we can substitute it into either of the 2 equations to find the value of the other variable, in this case .
We can also use the equation we had isolated, which is the most convenient for us since it gives us the value of x directly
And thus we obtain the value of our variables in a system of equations and note that the solution is UNIQUE.
Steps to Solve a 3x3 System of Linear Equations
1 Choose a variable and isolate it in one of the equations.
Generally, the variable with the smallest coefficient is chosen, and from the simplest equation, so that isolating it doesn't require so much algebraic work.
2 Substitute into the other two equations.
Use this isolated expression to substitute this variable in the other two equations. The two new equations resulting from this step will form a 2x2 system of equations.
3 We solve the 2x2 system.
For this we repeat the process:
- We choose one of the 2 variables and isolate it in one of the equations.
- We use this isolated expression to substitute the variable in the other equation (the one we didn't isolate in the 2x2 system).
- From the previous step we will get a linear equation with one variable, which when solved, we will obtain its value.
- We substitute the value we obtained into the isolated expression we made in this 2x2 system, and thus we will calculate the value of another variable.
4 We obtain the value of the missing variable
Since with step 3 we obtained the value of two of the three variables, to obtain the missing one we use the isolated expression we made in step one and substitute with the unknowns we already solved.
Exercises on Systems of 3 equations with 3 variables
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the third equation, which is the one with the smallest coefficient in the variable 
We use this isolated expression to substitute into the other 2 equations
By substituting into the second equation we obtain
This results in a new 2x2 system of equations
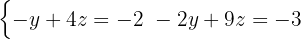
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. The simplest in this case is the first with the variable 
.
With this isolated expression we substitute into the other equation
Since we now have z=1, we use the last isolated expression we used to find y
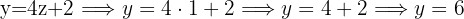
Now we take the first isolated expression we used, for the missing variable, in this case
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the first equation, which is the one with the smallest coefficient in the variable
We use this isolated expression to substitute into the other 2 equations
By substituting into the third equation we obtain
Substituting the value z=-1 into this last equation, we have
With this isolated expression we substitute into the first equation we isolated
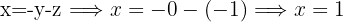
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the third equation, which is the one with the smallest coefficient in the variable
We use this isolated expression to substitute into the other 2 equations
By substituting into the second equation we obtain
This results in a new 2x2 system of equations
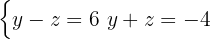
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. The simplest in this case is the first with the variable .
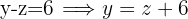
With this isolated expression we substitute into the other equation
Since we now have z=-5, we use the last isolated expression we used to find y
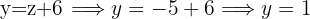
Now we take the first isolated expression we used, for the missing variable, in this case
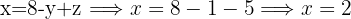
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the third equation, which is the one with the smallest coefficient in the variable
We use this isolated expression to substitute into the other 2 equations
By substituting into the second equation we obtain
Since we now have y=1, we use the last isolated expression we used to find z
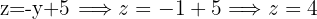
Now we take the first isolated expression we used, for the missing variable, in this case
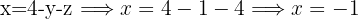
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the second equation, which is the one with the smallest coefficient in the variable
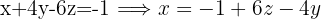
We use this isolated expression to substitute into the other 2 equations
We substitute into the next equation
This results in a new 2x2 system of equations
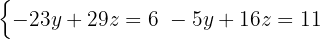
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. The simplest in this case is the second with the variable .
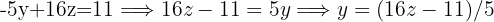
With this isolated expression we substitute into the other equation. To get rid of the denominator, it will be necessary to multiply the entire equation by 5
Since we now have , we use the last isolated expression we used to find y
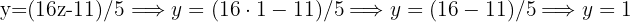
Now we take the first isolated expression we used, for the missing variable, in this case
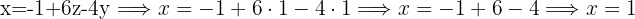
To apply the substitution method, we must choose an equation and a variable to isolate. Since it's convenient for the isolation to be simple, we choose the first equation, which is the one with the smallest coefficient in the variable
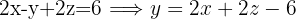
We use this isolated expression to substitute into the other 2 equations
This results in a new 2x2 system of equations
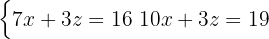
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. The simplest in this case is the first with the variable 
.
With this isolated expression we substitute into the other equation
Since we now have , we use the last isolated expression we used to find
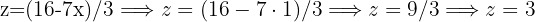
Now we take the first isolated expression we used, for the missing variable, in this case
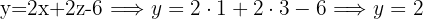
A supermarket customer has paid a total of $
for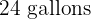 
of milk, 
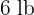of serrano ham and 
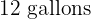of olive oil. Calculate the price of each item, knowing that 
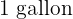of oil costs triple that of 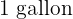of milk and that 
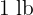of ham costs the same as 
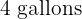of oil plus 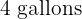of milk.
We declare the variables
Milk:
Ham:
Oil:
Each sentence gives us an equation which forms the following system of linear equations
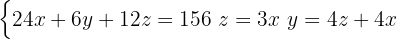
In this case, two of our equations already have variables isolated (Equation 2 and 3). We substitute the value of from the second equation into the third.
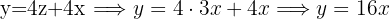
We substitute the value of and into the first equation
We use our isolated equations for and to obtain their values
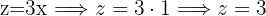
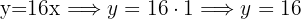
Finally
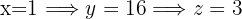
This means that the prices are
Milk $1
Ham $16
Oil $3
Pedro buys 2 notebooks, one pen and one folder for $
. If a notebook and a pen together cost $
more than the folder, and it is known that a notebook costs half the value of a folder. Find the price of each item.
We declare the variables
Notebook:
Pen:
Folder:
Each sentence gives us an equation which forms the following system of linear equations
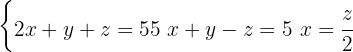
In this case, one of our equations already has a variable isolated (Equation 3). We substitute the value of from the third equation into the second.
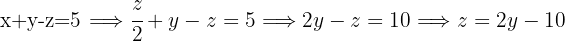
We substitute the value of and into the first equation
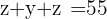
We use our isolated equations for and to obtain their values
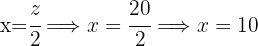
This means that the prices are
Notebook $10
Pen $15
Folder $20
A video store specializes in three types of movies: Children's, American Western and Horror. It is known that:
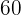of the children's movies plus 
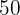of the western movies represent 
of the total movies. 
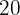of the children's plus 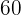of the western plus 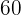of the horror movies represent half of the total movies.
If there are 
more western movies than children's movies. Find the number of movies of each type.
Each element of the exercise is assigned a variable.
Children's:
American Western:
Horror:
From the problem statement we obtain the 3x3 system of linear equations
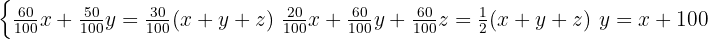
We rewrite and simplify the first equation
We multiply the entire equation by 100 to get rid of the only denominator and simplify the obtained expression:
We divide by 
and obtain:
We take the second equation and follow the same steps:
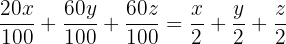
To have the same common denominator, we multiply the fractions on the right side by 
and obtain:
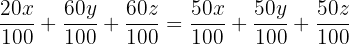
We get rid of the denominator and simplify:
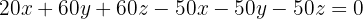
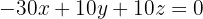
We divide the equation by and obtain:
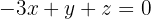
Using the simplified versions of the first and second equations, we form the following system:
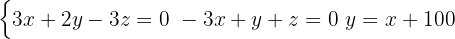
Since we already have a variable isolated in one of the equations, we use it to substitute the value of into the two initial equations and multiply the last obtained one by 3.
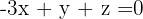
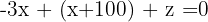
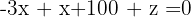
This results in a new 2x2 system of equations
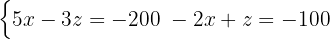
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. The simplest in this case is the second with the variable .
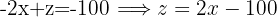
With this isolated expression we substitute into the other equation
Since we now have 
, we use the last isolated expression we used to find
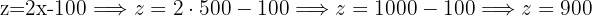
Now we take the first isolated expression we made, for the missing variable, in this case
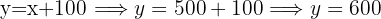
Finally we conclude that there are
Children's 500 movies
Western 600 movies
Horror 900 movies
The sides of a triangle measure 
, 
and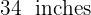 
. With center at each vertex, three circles are drawn, tangent to each other two by two. Calculate the lengths of the radii of the circles.
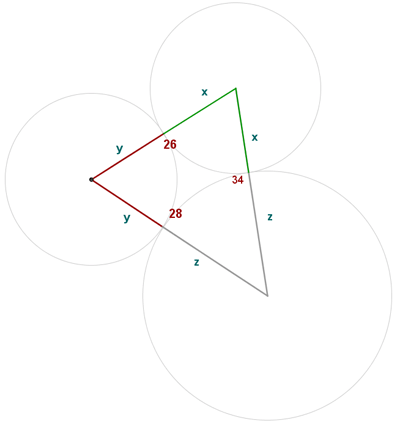
From making a sketch of the figure, and using a variable for each radius of the 3 circles, we have the system
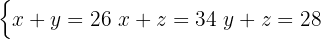
To apply the substitution method, we must choose an equation and a variable to isolate. We will isolate in this case the variable from the first equation
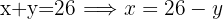
We use this isolated expression to substitute into the other 2 equations
In this case the equation doesn't have variable x, so we leave it as is.
From this we have a new 2x2 system of equations
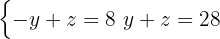
Here we must apply the substitution method again, that is, choose an equation and a variable to isolate. One of the simplest in this case is the second with the variable .
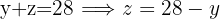
With this isolated expression we substitute into the other equation
Since we now have 
, we use the last isolated expression we used to find
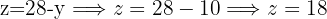
Now we take the first isolated expression we made, for the missing variable, in this case
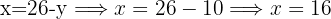
✨ Count on Superprof to get the best math courses.
Did you like this article? Rate it!
Loading...
