A first-degree equation (also known as a linear equation, since its graph is a straight line) is an equality between two algebraic expressions that contain one or more unknown variables — each raised to the power of  . These variables are related through basic arithmetic operations.
. These variables are related through basic arithmetic operations.

Solved Exercises on First-Degree Equations

We isolate the unknown by dividing both sides of the equation by  . Practically speaking, we can say that the
. Practically speaking, we can say that the  multiplying the variable on the left-hand side "goes to the other side dividing."
multiplying the variable on the left-hand side "goes to the other side dividing."


We group like terms. We need to add  and
and  to both sides to obtain an equivalent equation.
to both sides to obtain an equivalent equation.
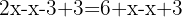
In practice, it is often said that if a term is added on one side, like  , it "moves to the other side subtracting" (becomes
, it "moves to the other side subtracting" (becomes  ), and if it's subtracted, like
), and if it's subtracted, like  , it "moves to the other side adding" (becomes
, it "moves to the other side adding" (becomes  ).
).
We then simplify:



We use the distributive property to eliminate the parentheses — that is, multiply each term inside the parentheses by  . On the left-hand side, we get:
. On the left-hand side, we get:
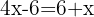
Now we group like terms: move the  from the right to the left as
from the right to the left as  , and move the
, and move the  to the right as
to the right as 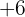 .
.

We isolate the unknown — the  multiplying the variable "goes to the other side dividing":
multiplying the variable "goes to the other side dividing":

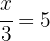
We isolate the unknown:
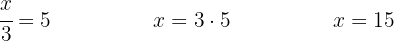
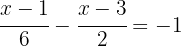
To eliminate the denominators, we must find the least common multiple (LCM) of  and
and  :
:
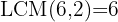
We multiply both sides of the equation by the LCM, in this case  , and obtain:
, and obtain:
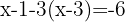
We apply the distributive property to resolve the parentheses, group like terms, and simplify:
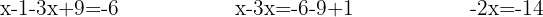
We isolate the unknown:
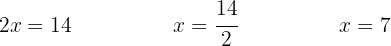
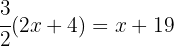
We multiply  by each term inside the parentheses (distributive property) to resolve the expression and simplify:
by each term inside the parentheses (distributive property) to resolve the expression and simplify:

We group and combine like terms:
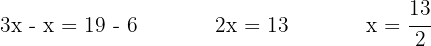

Using the distributive property, we expand the parentheses by multiplying the first by  and the second by
and the second by  :
:
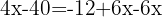
We group like terms:
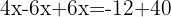
Combine like terms and isolate the variable:


Using the distributive property to eliminate parentheses, we multiply the first by  and the second by
and the second by  :
:

We group like terms:
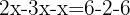
Combine like terms and isolate the variable:

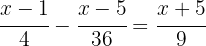
To eliminate the denominators, we need the least common multiple (LCM) of  ,
,  , and
, and  :
:
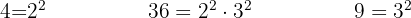
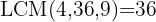
We divide the LCM by each denominator and multiply the result by the corresponding numerator:
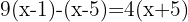
Using the distributive property, we multiply the first term by  , the second by
, the second by  , and the third by
, and the third by  :
:
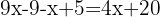
Group like terms:

Combine and isolate:

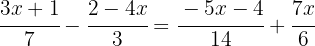
To eliminate the denominators, we find the least common multiple (LCM) of  ,
,  ,
,  , and
, and  :
:

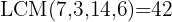
We divide the LCM by each denominator and multiply by the corresponding numerator:

Apply the distributive property to expand all expressions:
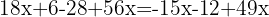
Group like terms:

Simplify and isolate:
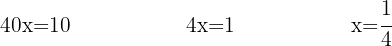
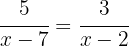
For the equality between the two fractions to hold, the product of the extremes must be equal to the product of the means.
Or, if preferred, we can also find the LCM, which is  because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator:
because both binomials are irreducible. Then we divide the LCM by each denominator and multiply the result by the corresponding numerator:
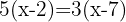
Using the distributive property to expand the parentheses, we multiply the first parenthesis by  and the second by
and the second by  :
:
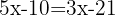
We combine like terms:
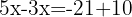
Solving for the unknown:

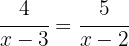
For the equality between two fractions to hold, the product of the extremes must equal the product of the means.
Alternatively, we can find the least common multiple, which is 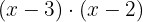 because both binomials are irreducible. We then divide the LCM by each denominator and multiply the result by the corresponding numerator.
because both binomials are irreducible. We then divide the LCM by each denominator and multiply the result by the corresponding numerator.
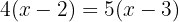
Using the distributive property to expand the parentheses, we multiply the first one by  and the second by
and the second by  :
:
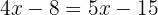
Group like terms:

Isolate the unknown:
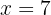
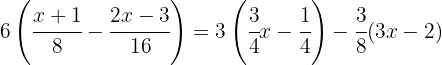
Using the distributive property to expand the parentheses, we multiply the first by  , the second by
, the second by  , and the third by
, and the third by  .
.
Remember that when multiplying an integer by a fraction, we multiply the integer by the numerator and keep the same denominator.
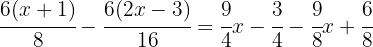
Apply the distributive property in the numerators:
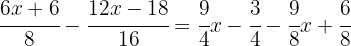
To eliminate the denominators, we find the least common multiple of  ,
,  , and
, and  :
:
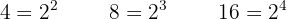
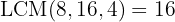
We divide the LCM by each denominator and multiply by the corresponding numerator:
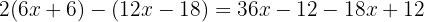
Apply the distributive property and simplify carefully with sign changes:

Group like terms:
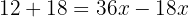
Isolate the unknown:
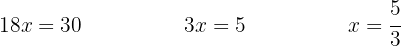
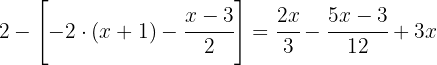
In this case, it’s convenient to start by expanding the expression 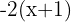 . After simplifying, we can replace the bracket with a parenthesis:
. After simplifying, we can replace the bracket with a parenthesis:
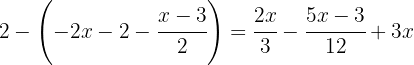
We multiply all the terms inside the parenthesis by  to remove the minus sign and parentheses:
to remove the minus sign and parentheses:
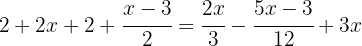
To eliminate denominators, we find the least common multiple of  ,
,  , and
, and  :
:
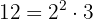
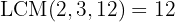
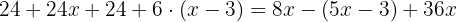
Using the distributive property, we multiply the first parenthesis by  and the second by
and the second by  :
:
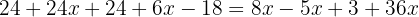
Group like terms:
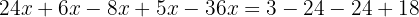
Simplify:

Divide both sides by  :
:
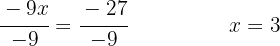
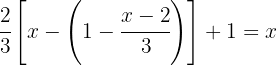
We multiply the terms inside the parenthesis by  to eliminate the minus sign and parentheses, then replace the bracket with a parenthesis:
to eliminate the minus sign and parentheses, then replace the bracket with a parenthesis:
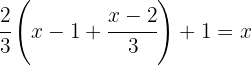
Apply the distributive property:
(Remember: when multiplying one fraction by another, multiply the numerators and denominators directly.)
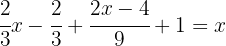
To eliminate the denominators, we find the LCM of  and
and  :
:

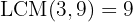

Group like terms:

Simplify and solve:

If you need help with math, don’t hesitate to check out Superprof. You’ll find top-rated tutors — both online and in person — to support your learning.












