Solved Problems Using Newton's Laws

Welcome to the fascinating world of Newton's laws! In this set of solved exercises, we will explore the fundamental laws that govern the motion of objects in our universe. Sir Isaac Newton revolutionized our understanding of motion and the interaction of forces, establishing three laws that are the foundation of classical mechanics.

Through these exercises, we will discover how to apply Newton's laws to understand and predict the behavior of objects at rest and in motion. From force analysis to determining accelerations and solving practical problems.

Let's begin:

1 A car moves at a constant speed of 50 km/h (31 mph). Find the net velocity.

Solution

1 Newton's first law states that a body at rest remains at rest, or if it is in motion with constant velocity it remains in motion, unless a net force acts on it.

2 Since the car is in motion with constant velocity, then the net force on it is zero. We note that the car has a forward driving force, but there is also an opposing force called friction force that has the same magnitude and opposite direction to the driving force, so that the net force is zero.

2 A 5 kg (11 lb) lamp hangs from a wire embedded in the ceiling. What is the tension in the wire?

Solution

1 We draw the equilibrium diagram

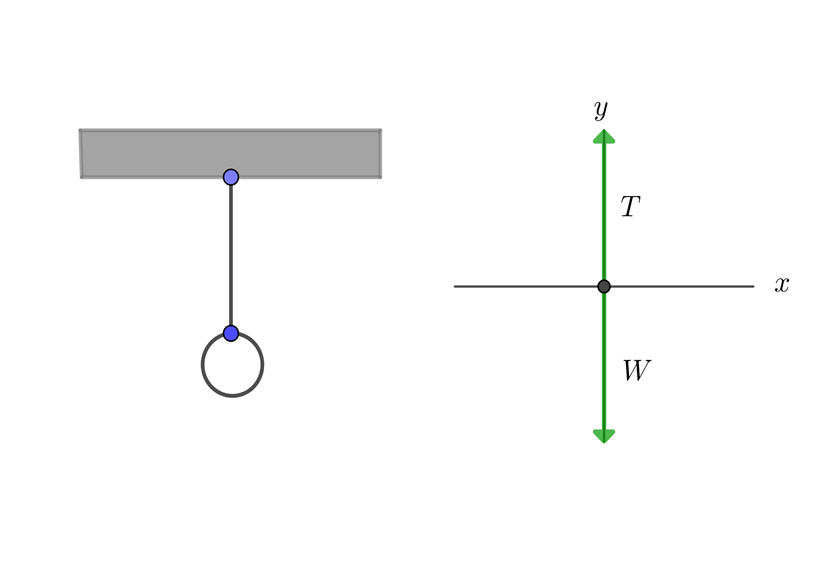
2 We know the mass of the lamp, so we calculate its weight W

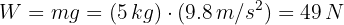
3 We calculate the net vertical force, since there are no horizontal forces acting

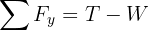
4 Since the system is in equilibrium, the net force equals zero

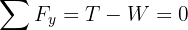
5 Solving we obtain T=49 N (11 lbf)

Note that being in equilibrium, the net force is zero so both forces being opposite, they are equal in magnitude.

3 A cable embedded in the ceiling supports an object of mass m, which has a cable supporting another object that has half its mass. What is the tension in the cables?

Solution

1 We draw the equilibrium diagram

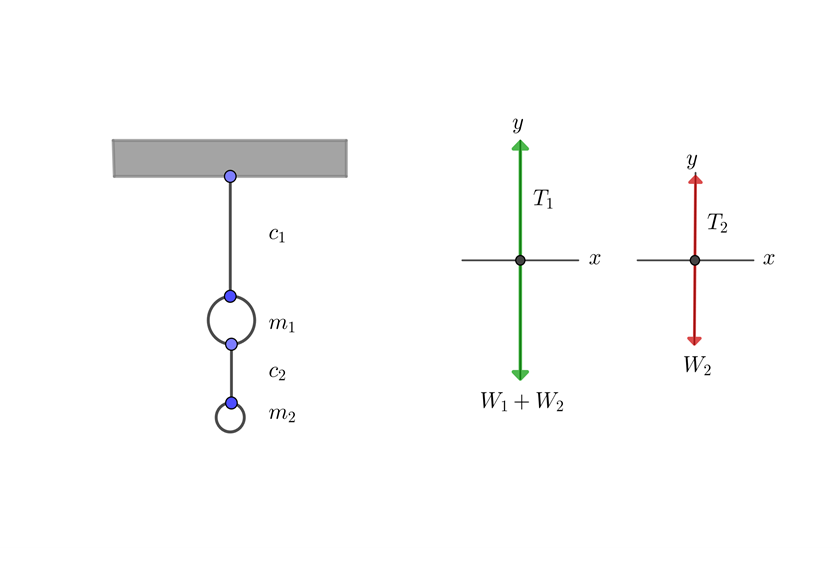
2 We know the mass of the objects, so we calculate their weight

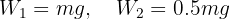
3 We calculate the net vertical force for the first system, since there are no horizontal forces acting

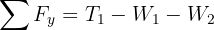
4 Since the system is in equilibrium, the net force equals zero

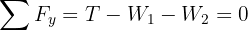
5 Solving we obtain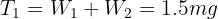

6 For the second system where the second cable and second mass interact, since the net force is zero, then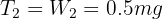

4 A box suspended by a rope is pulled to the right horizontally with another rope and held so that the first rope forms an angle 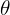with the ceiling. If the box has mass m, find the tensions in both ropes.

Solution

1 We draw the equilibrium diagram

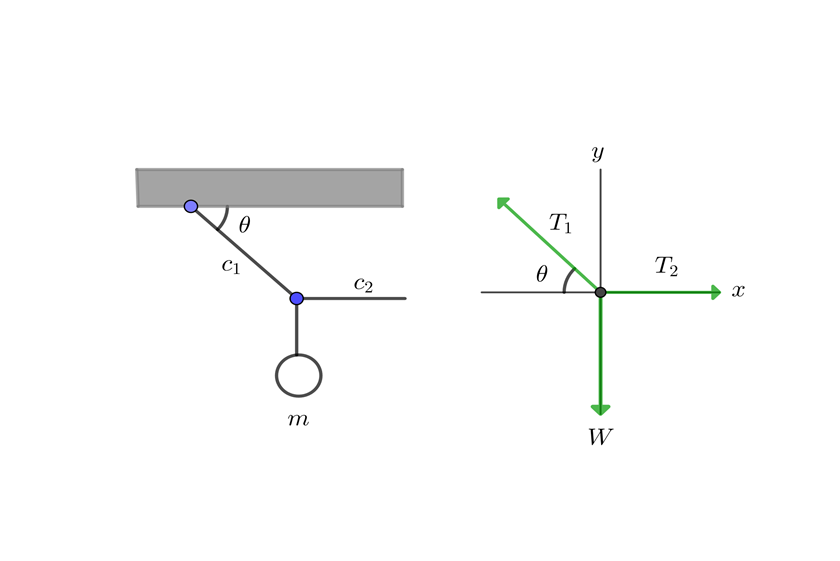
2 We know the mass of the box, so we calculate its weight and calculate the components of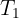

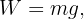
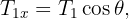
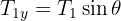
3 We calculate the horizontal and vertical net force

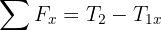
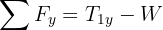
4 Since the system is in equilibrium, the net forces equal zero

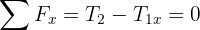
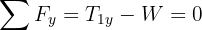
5 Solving for 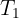in the vertical net force, we obtain

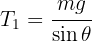
6 Solving for 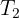in the horizontal net force, we obtain

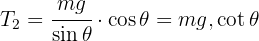
5 A piñata suspended by a rope is pulled to the right horizontally with another rope and held so that the first rope forms an angle 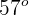with the ceiling. If the weight of the piñata is 9.8 N (2.2 lbf), find the tensions in both ropes.

Solution

1 We draw the equilibrium diagram

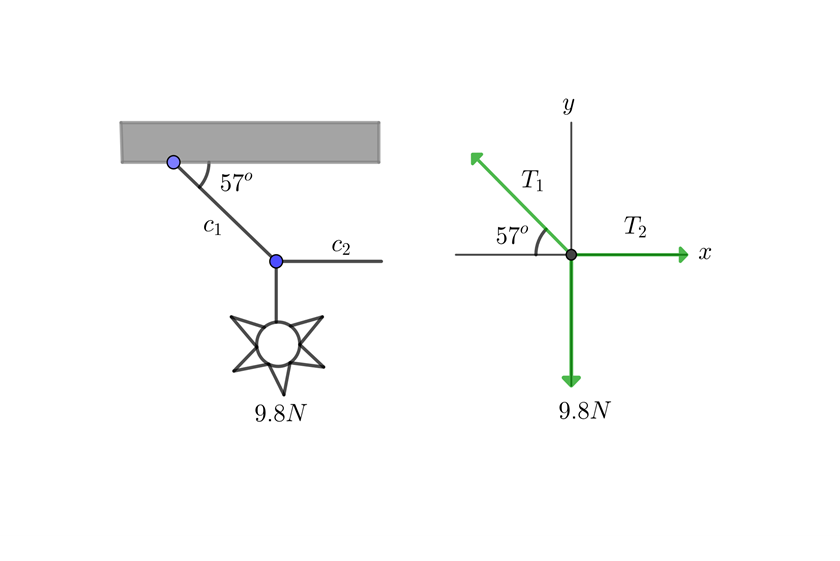
2 We calculate its weight and calculate the components of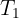

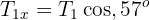
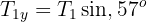
3 We calculate the horizontal and vertical net force

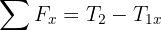
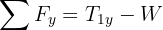
4 Since the system is in equilibrium, the net forces equal zero

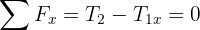
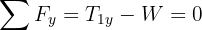
5 Solving for 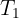in the vertical net force, we obtain

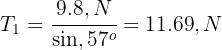
6 Solving for 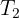in the horizontal net force, we obtain

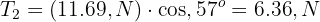
6 An object hangs from a rope attached to two other ropes fixed to a ceiling, forming a triangle. If the box has a weight W and the angles of the two ropes with the ceiling are 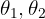respectively, find the tensions of the three ropes.

Solution

1 We draw the equilibrium diagram

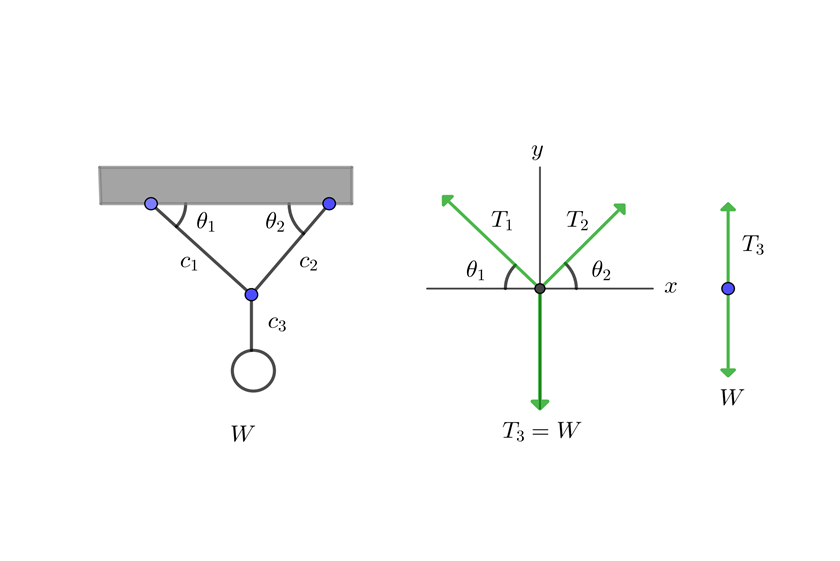
2 From the vertical system formed by the object and rope three, we obtain

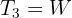
3 Considering the three ropes, we have a system whose components are

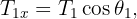
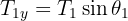
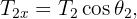
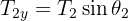
4 We calculate the horizontal and vertical net force

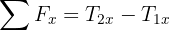
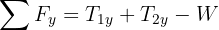
5 Since the system is in equilibrium, the net forces equal zero

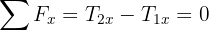
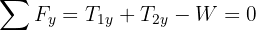
6 In terms of 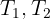the system of equations obtained is

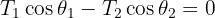
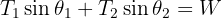
7 Solving the system for 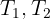, we obtain

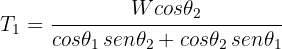
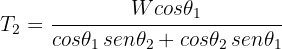
7 An object hangs from a rope attached to two other ropes fixed to a ceiling, forming a triangle. If the box has a weight of 100 N (22.5 lbf) and the angles of the two ropes with the ceiling are 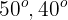respectively, find the tensions of the three ropes.

Solution

1 We draw the equilibrium diagram

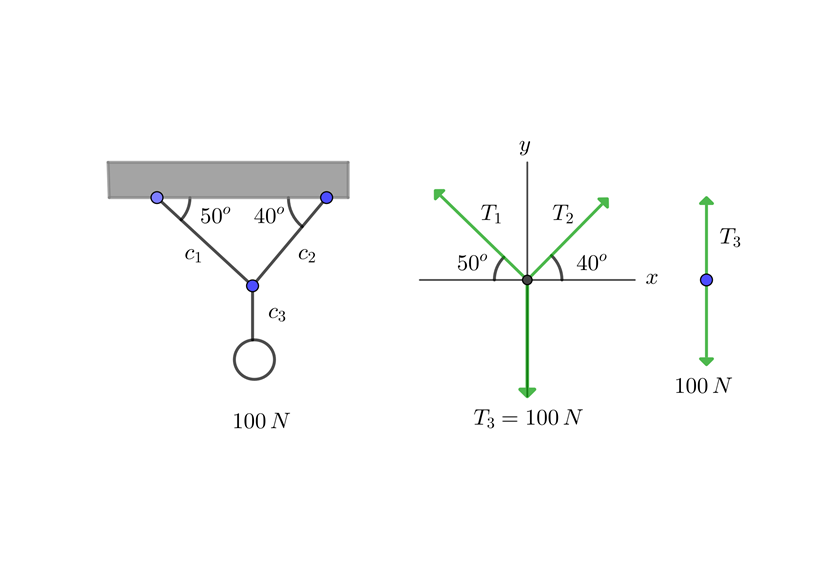
2 We note that the conditions of problem 6 are satisfied, so we substitute into the formulas found in that exercise

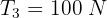
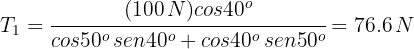
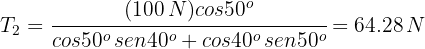
8 An object of weight W is on a frictionless inclined plane with slope 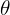. The object is tied to a rope that passes over a frictionless pulley placed at the upper end of the plane and is attached to a block. If the system is in equilibrium, find the weight of the block.

Solution

1 We draw the equilibrium diagram

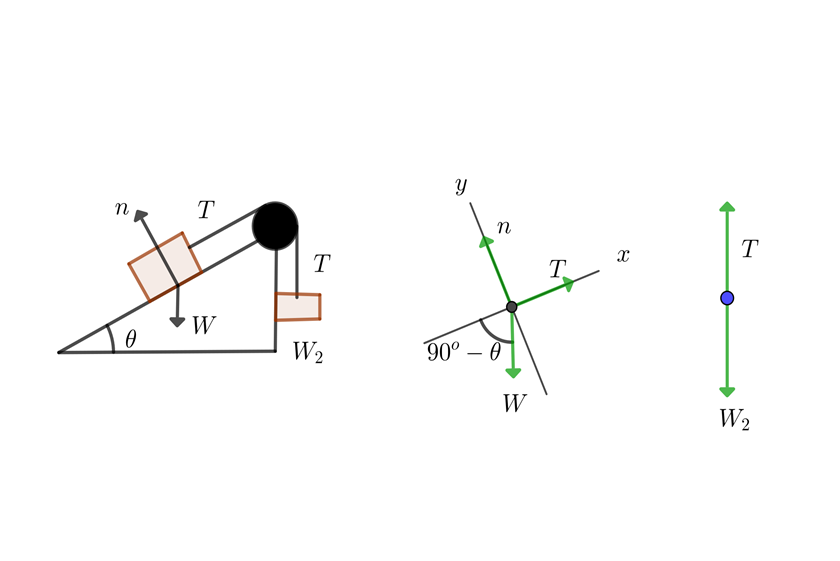
2 From the vertical system formed by the object and the rope, we obtain

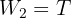
3 Considering the object on the inclined plane, we have a system whose weight components are

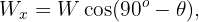
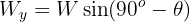
4 We calculate the horizontal and vertical net force

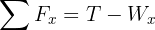
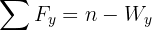
5 Since the system is in equilibrium, the net forces equal zero

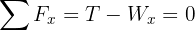
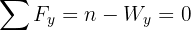
6 From the first equation we have that 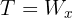, then the weight of the block is

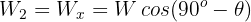
9 An object of weight 50 N (11.2 lbf) is on a frictionless inclined plane with slope . The object is tied to a rope that passes over a frictionless pulley placed at the upper end of the plane and is attached to a block. If the system is in equilibrium, find the weight of the block.

Solution

1 We draw the equilibrium diagram

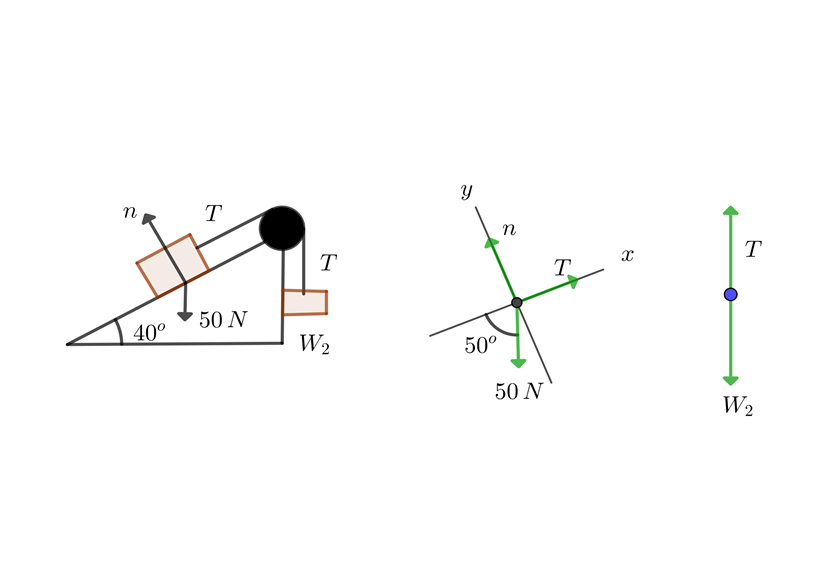
2 We note that the conditions of problem 8 are satisfied, so we substitute into the formula found in that exercise

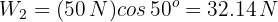
10 An object is on a frictionless inclined plane with slope 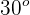. The object is tied to a rope that passes over a frictionless pulley placed at the upper end of the plane and is attached to a 100 N (22.5 lbf) block. If the system is in equilibrium, find the weight of the object on the plane.

Solution

1 We draw the equilibrium diagram

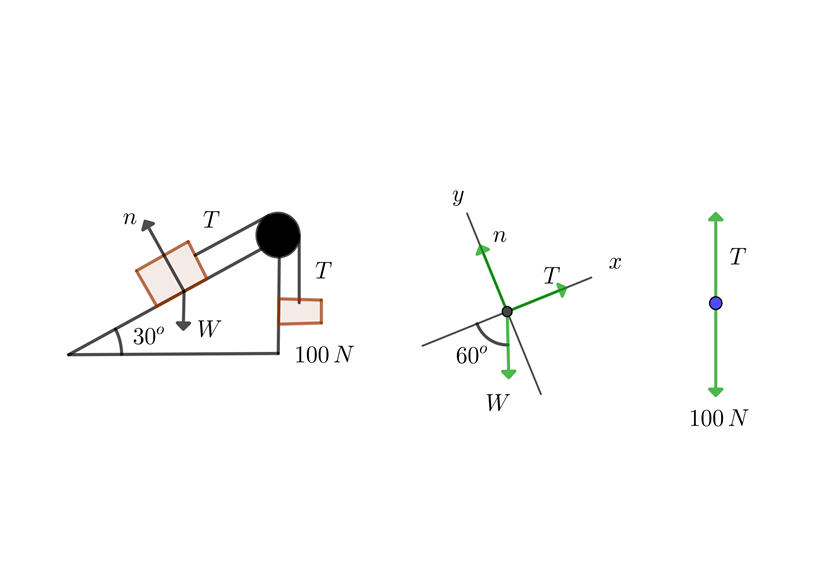
2 We note that the conditions of problem 8 are satisfied, so we substitute into the formulas found in that exercise and solve for the weight