Test your knowledge of second-degree equations with our excellent equations! Make sure to practice frequently and reach out to a Superprof tutor if you need additional help, to make sure you get an A+ on your next assignment.

Review of the General Formula
To solve the proposed exercises, we’ll use the general formula for quadratic equations:

This formula is used to solve any second-degree equation of the form:
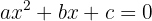 where
where 
Using this method is very simple — we just need to set the equation equal to zero and substitute the values of a, b, and c into the formula.
When solving a quadratic equation, three scenarios are possible:
- There are two values for the variable x that satisfy the equation.
- There is only one solution.
- The solution does not belong to the set of real numbers.
Quadratic Equation Exercises

1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We identify the values of a, b and c

2 We substitute in the general formula and solve



3 The equation has no solution in the real numbers

1 We identify the values of a, b and c

2 We substitute in the general formula and solve



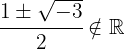
3 The equation has no solution in the real numbers

1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two equal real solutions


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions

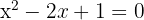
1 We identify the values of a, b and c

2 We substitute in the general formula and solve


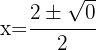


3 The equation has only one real solution


1 We identify the values of a, b and c

2 We substitute in the general formula and solve




3 The equation has no solution in the real numbers.

1 We identify the values of a, b and c

2 We substitute in the general formula and solve




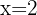
3 The equation has only one real solution.
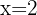

1 We move all terms to one side of the equation to have it in the form 

2 We identify the values of a, b and c

3 We substitute in the general formula and solve




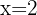
4 The equation has only one real solution.
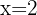

1 We solve the binomial squared

2 We move all terms to one side and group them to write the equation in the form 

3 We identify the values of a, b and c

4 We substitute in the general formula and solve
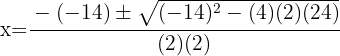




5 The equation has two real solutions.


1 In this case, we can divide both sides of the equation by 7 to simplify it

2 We identify the values of a, b and c

3 We substitute in the general formula and solve





4 The equation has two real solutions.


1 We multiply both sides by −1 to obtain an equivalent equation with a > 0


2 The equation has no real solutions

1 We use the distributive property to operate the parenthesis and obtain:

2 We operate and move everything to the first member

3 We identify the values of a, b and c

4 We substitute in the general formula and solve





5 The equation has two real solutions.


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We solve the binomial squared

2 We move all terms to one side and group them to write the equation in the form 

3 We divide both sides of the equation by 2 to simplify it

4 We identify the values of a, b and c

5 We substitute in the general formula and solve





6 The equation has two real solutions.


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We identify the values of a, b and c

2 We substitute in the general formula and solve





3 The equation has two distinct real solutions


1 We multiply the first member of the equation by 6, and the last by 2 to eliminate the denominator (6), and thus we obtain:

2 We identify the values of a, b and c

3 We substitute in the general formula and solve





4 The equation has two real solutions.

Remember, at Superprof you can also find math classes with a tutor who can adapt to your needs.












