Projectile motion is a physical phenomenon that describes the movement of an object launched at an angle with respect to the horizontal. This type of motion follows a curved path known as a parabola, and its study is essential in fields such as physics and engineering. Projectile motion exercises are a fundamental tool for understanding and applying the principles of kinematics and dynamics in practical situations.
In these exercises, concepts such as the maximum height reached by the projectile, horizontal range, initial velocity, and launch angle are explored.
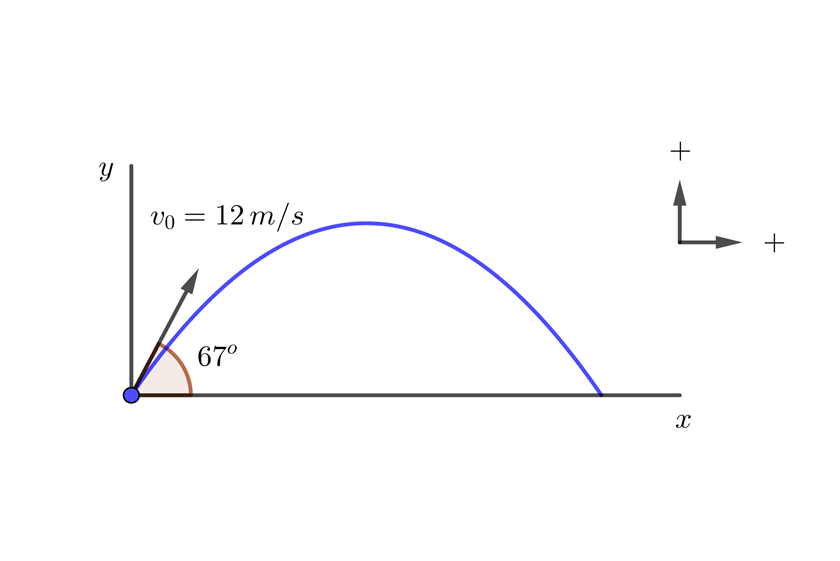
A ball is thrown at 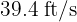 and at an angle of
and at an angle of 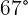 with respect to the horizontal. What is its height at 2 seconds?
with respect to the horizontal. What is its height at 2 seconds?
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 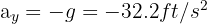 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data:
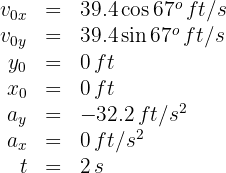
3. To calculate the height, we use the formula:
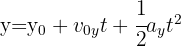
4. We substitute the known data:
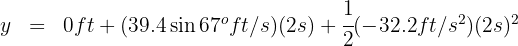
from which we obtain 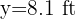 .
.
A plane with velocity of 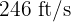 drops a supply box at
drops a supply box at 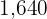 feet above the ground. What is the displacement of the box at 2 seconds?
feet above the ground. What is the displacement of the box at 2 seconds?
1. We establish downward and rightward directions as positive; thus, the vertical acceleration is 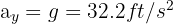 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
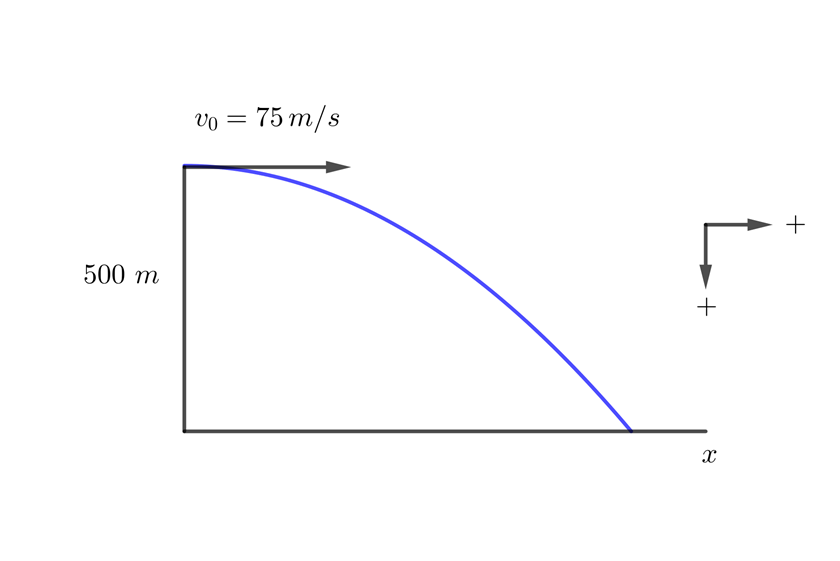
2. We indicate the known data:
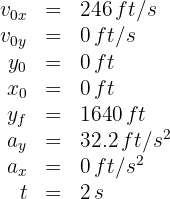
3. To calculate the distance traveled by the box in 2 seconds, we use the formula:
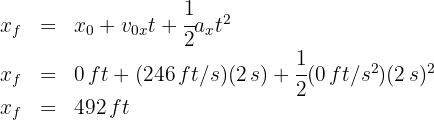
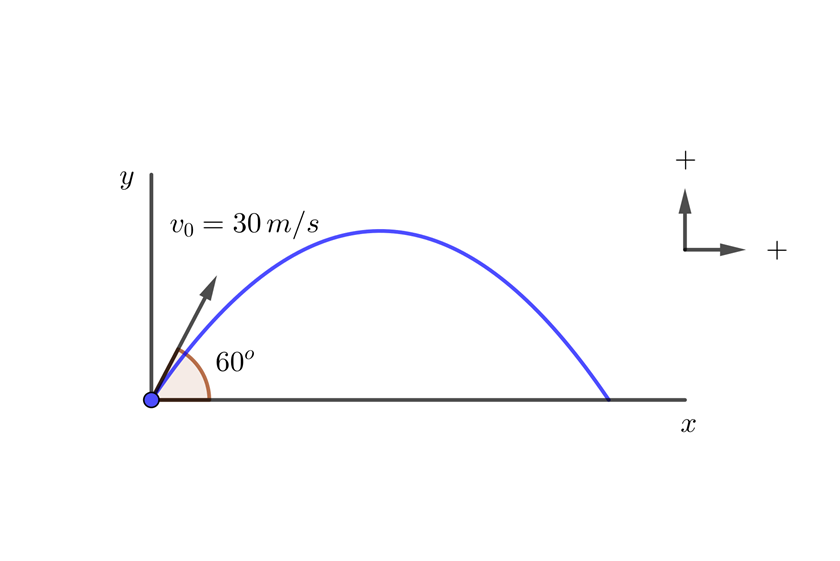
A projectile is launched from ground level at an angle of 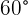 with respect to the ground. The initial velocity of the projectile is
with respect to the ground. The initial velocity of the projectile is 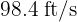 . What is the maximum height reached by the projectile and how long does it take to reach it?
. What is the maximum height reached by the projectile and how long does it take to reach it?
1. The maximum height of the projectile is found using the vertical part of the motion. We establish upward and rightward directions as positive; thus, the vertical acceleration is 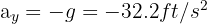 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data: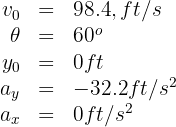
3. We calculate the horizontal and vertical components of the initial velocity: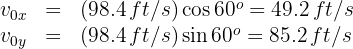
4. We note that upon reaching its maximum height: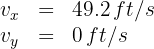
5. Since the acceleration is constant in the vertical part of the motion, we have a uniformly accelerated motion problem, so we use the formula: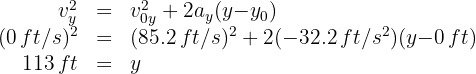
6. To find the time, we use: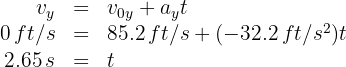
An NFL player punts the ball with an initial velocity of 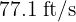 at an angle of
at an angle of 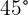 with respect to the ground. What is the flight time of the ball? What is the horizontal range of the ball?
with respect to the ground. What is the flight time of the ball? What is the horizontal range of the ball?
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 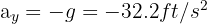 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
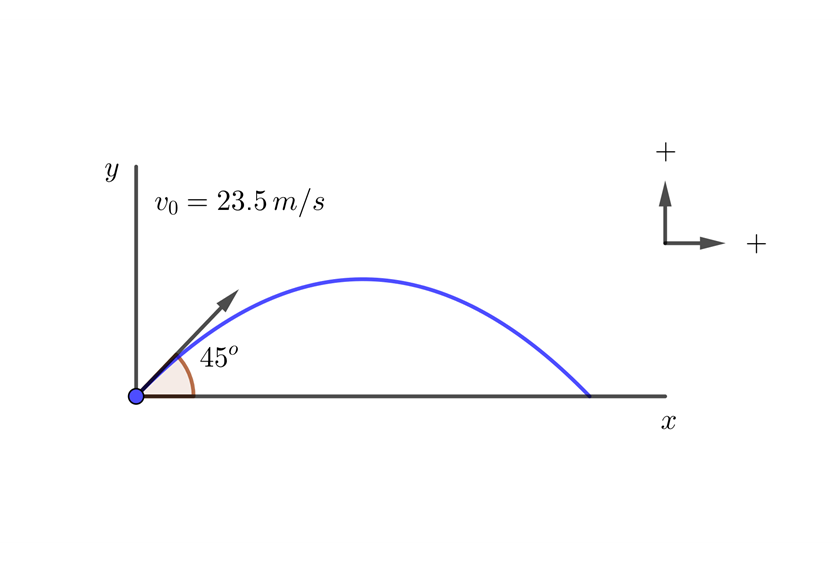
2. We indicate the known data:
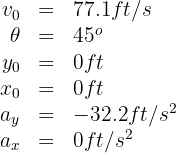
3. We calculate the horizontal and vertical components of the initial velocity:
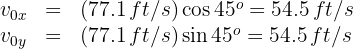
4. We note that to find the flight time:
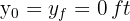
5. Since the acceleration is constant in the vertical part of the motion, we have a uniformly accelerated motion problem, so we substitute the known data into the formula:
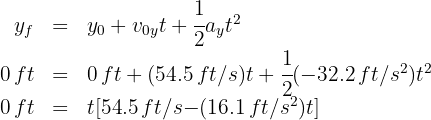
from which we obtain  and
and 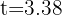 seconds, which correspond to the initial and final positions of the ball, respectively.
seconds, which correspond to the initial and final positions of the ball, respectively.
6. To find the horizontal range, we use:
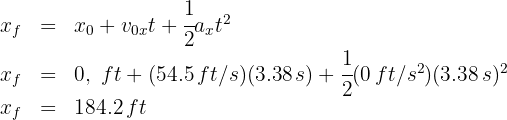
In the NFL, distance is measured in yards, so the horizontal range equals 61.4 yards.
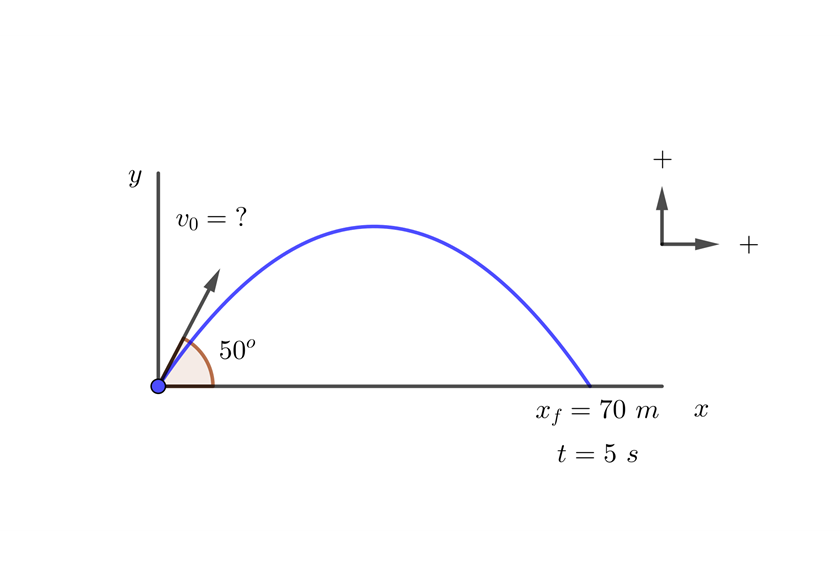
A soccer player is 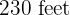 from the opposing goal and in possession of the ball. He observes that the goalkeeper is outside the penalty area and estimates it will take at least
from the opposing goal and in possession of the ball. He observes that the goalkeeper is outside the penalty area and estimates it will take at least 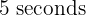 for him to return to the goal. If the player kicks the ball at
for him to return to the goal. If the player kicks the ball at 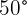 with respect to the ground, find the velocity at which he must kick the ball for it to enter the goal.
with respect to the ground, find the velocity at which he must kick the ball for it to enter the goal.
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 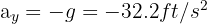 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data:
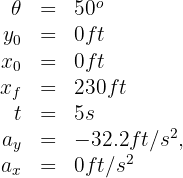
3. We express in terms of 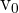 the horizontal and vertical components of the initial velocity:
the horizontal and vertical components of the initial velocity:
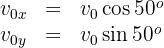
4. Since the acceleration is zero in the horizontal part of the motion, the velocity is constant and we have a uniform motion problem, so we substitute the known data into the formula:
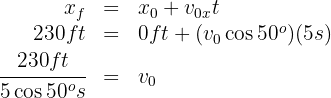
from which we obtain 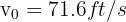 .
.
A baseball player throws the ball at an angle of 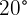 with respect to the horizontal at
with respect to the horizontal at 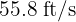 . If a teammate catches the ball at the same height it was thrown, how far apart are both players?
. If a teammate catches the ball at the same height it was thrown, how far apart are both players?
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 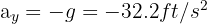 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
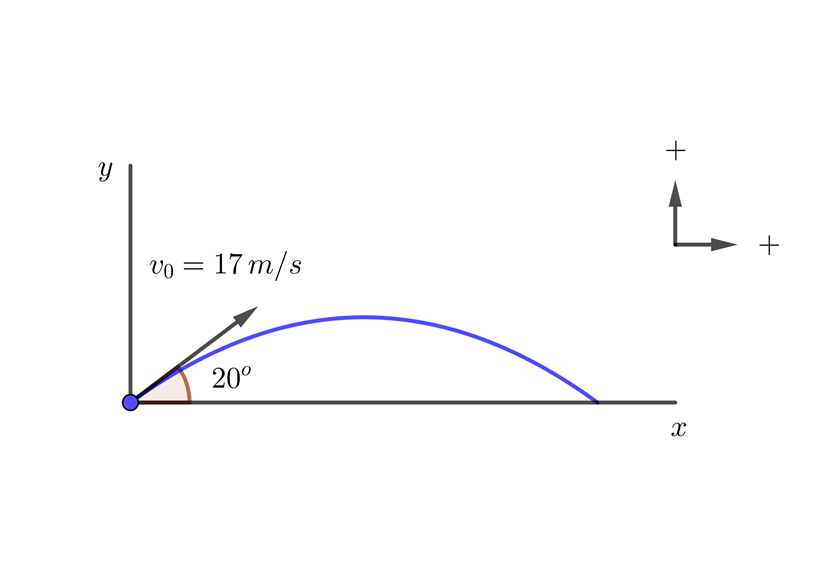
2. We indicate the known data:
3. We calculate the horizontal and vertical components of the initial velocity:
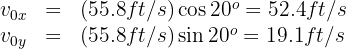
4. The distance between the two baseball players equals the horizontal range. To find this range, we need the flight time:
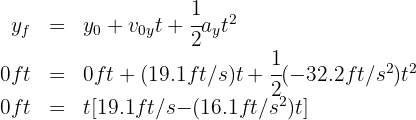
from which we obtain  and
and 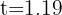 seconds, which correspond to the initial and final positions of the ball, respectively.
seconds, which correspond to the initial and final positions of the ball, respectively.
5. To find the horizontal range, we use:
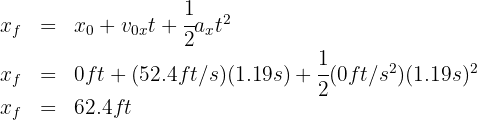
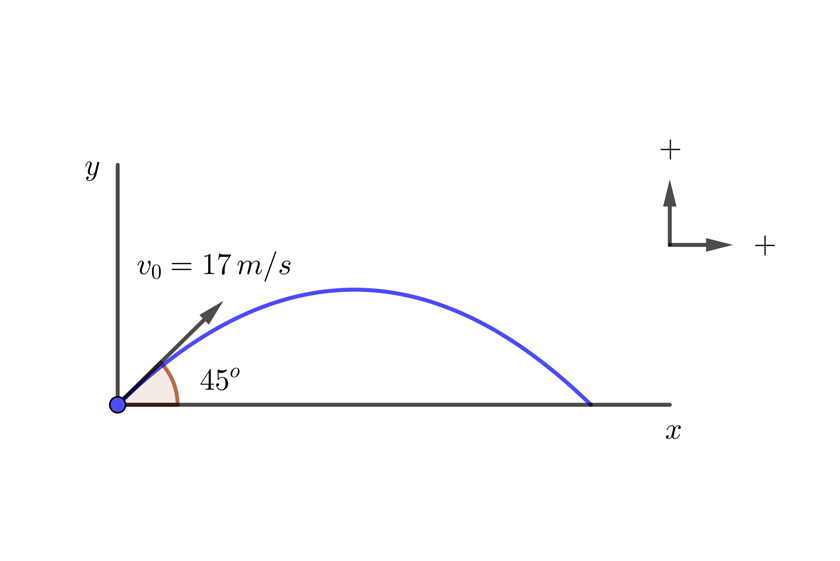
A ball is kicked from the ground at an angle of 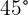 and with an initial velocity of
and with an initial velocity of 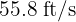 . What is the horizontal range of the ball?
. What is the horizontal range of the ball?
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 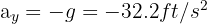 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data:
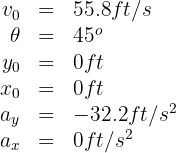
3. We calculate the horizontal and vertical components of the initial velocity:
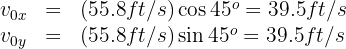
4. To find this range, we need the flight time:
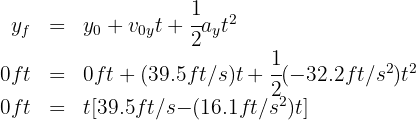
from which we obtain  and
and 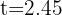 seconds, which correspond to the initial and final positions of the ball, respectively.
seconds, which correspond to the initial and final positions of the ball, respectively.
5. To find the horizontal range, we use:
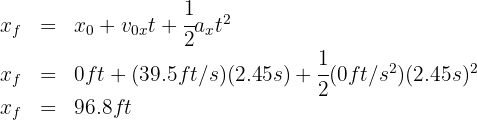
Two projectiles are launched from the ground, both with initial velocity of 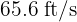 and angles of
and angles of 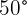 and
and 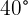 . How do the ranges of both projectiles compare?
. How do the ranges of both projectiles compare?
1. We establish upward and rightward directions as positive; thus, the vertical acceleration is 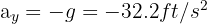 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data:
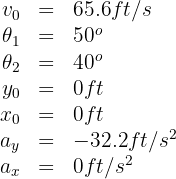
3. We calculate the horizontal and vertical components of the initial velocity of the first projectile:
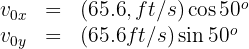
For the second projectile:
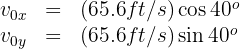
4. To find the range, we need the flight time. For the first projectile:
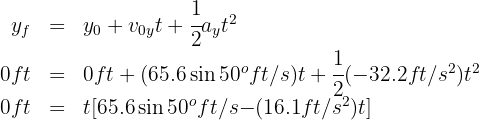
from which we obtain  and
and 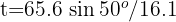 seconds, which correspond to the initial and final positions of the ball, respectively.
seconds, which correspond to the initial and final positions of the ball, respectively.
For the second projectile:
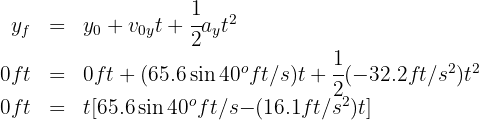
from which we obtain  and
and 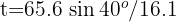 seconds, which correspond to the initial and final positions of the ball, respectively.
seconds, which correspond to the initial and final positions of the ball, respectively.
5. The horizontal range of the first projectile:

The horizontal range of the second projectile:

Thus, both horizontal ranges are equal. In fact, the ranges of any two complementary angles are equal.
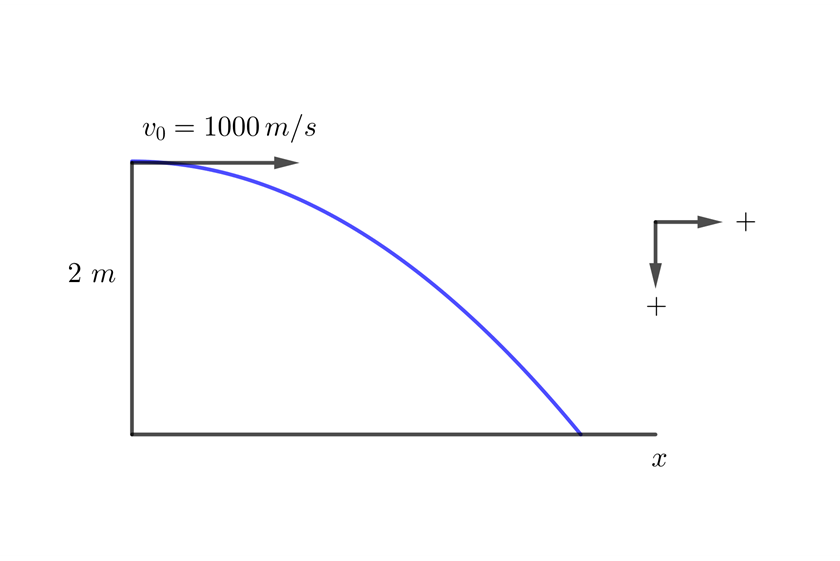
A bullet is fired horizontally at 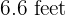 above ground level. If the initial velocity of the bullet is
above ground level. If the initial velocity of the bullet is 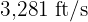 , how long does it take for the bullet to hit the ground?
, how long does it take for the bullet to hit the ground?
1. We establish downward and rightward directions as positive; thus, the vertical acceleration is 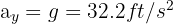 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.
2. We indicate the known data:
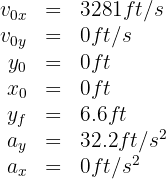
3. To calculate the flight time, we use the formula:
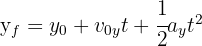
4. We substitute the known data:
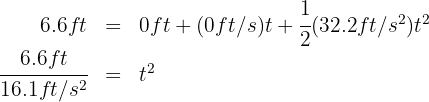
from which we obtain 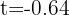 and
and 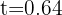 seconds. We choose the positive time, since negative time makes no sense.
seconds. We choose the positive time, since negative time makes no sense.
A plane with velocity of 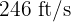 drops a supply box at
drops a supply box at 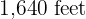 above the ground. What is the displacement of the box?
above the ground. What is the displacement of the box?
1. We establish downward and rightward directions as positive; thus, the vertical acceleration is 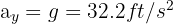 . The horizontal acceleration is always zero, so the horizontal velocity is constant.
. The horizontal acceleration is always zero, so the horizontal velocity is constant.

2. We indicate the known data:
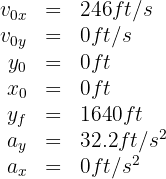
3. To calculate the flight time, we use the formula:
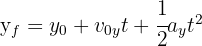
4. We substitute the known data:
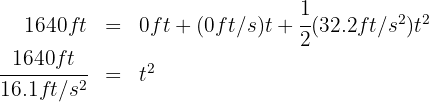
from which we obtain 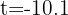 and
and 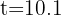 seconds. We choose the positive time, since negative time makes no sense.
seconds. We choose the positive time, since negative time makes no sense.
5. To calculate the distance traveled by the box, we use the formula:
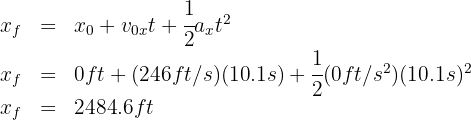
Summarize with AI:


