Chapters
1
2
3
4
5
6
Practice Exercises
Simplify using the laws of exponents
1 
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
1
To multiply powers with the same base we keep the same base and add the exponents 
2
To divide powers with the same base we keep the same base and subtract the exponents 
3
To find the power of a power we multiply the exponents 
4
To find the power of a product, we raise each element to the given power 
5
To find the power of a power we multiply the exponents 
6
To find the power of a power we multiply the exponents 
7
First we express the base as a product of prime numbers and then find the power of a power by multiplying the exponents 
8
First we express the base as a product of prime numbers and then find the power of a power by multiplying the exponents 
9
To multiply powers with the same base we keep the same base and add the exponents 
10
To divide powers with the same base we keep the same base and subtract the exponents 
11
We find the power of a power by multiplying the exponents 
12
To find the power of a product, we raise each element to the given power 
13
To find the power of a power we multiply the exponents 
14
First we find the power of a power by multiplying the exponents and apply that any number different from zero raised to the power zero equals one 
15
First we express the base as a product of prime numbers and then find the power of a power by multiplying the exponents 
16
First we express the base as a product of prime numbers and then find the power of a power by multiplying the exponents 
Perform the following operations with powers:
1
2
3
4
5
6
7
8
9
10
1
To multiply powers with the same base we keep the same base and add the exponents 
The result will have a negative sign because the base is negative and the exponent is odd
2
First we decompose 8 into factors and then multiply powers with the same base 
The result will have a positive sign because the base is negative and the exponent is even
3
To multiply powers with the same base we keep the same base and add the exponents 
The result will have a negative sign because the base is negative and the exponent is odd
4
To multiply powers with the same base we keep the same base and add the exponents 
Since the exponent is negative, we have to take the reciprocal of the base 
5
To divide powers with the same base we keep the same base and subtract the exponents 
Since the exponent is negative, we have to take the reciprocal of the base
6
To divide powers with the same base we keep the same base and subtract the exponents 
Since the exponent is negative, we have to take the reciprocal of the base with positive exponent and develop
7
To divide powers with the same base we keep the same base and subtract the exponents 
8
To divide powers with the same base we keep the same base and subtract the exponents 
9
To raise a power to a power we keep the same base and multiply the exponents 
To divide powers with the same base we keep the same base and subtract the exponents 
10
We solve the brackets so to divide powers with the same base we keep the same base and subtract the exponents 
To raise a power to a power we keep the same base and multiply the exponents 
The result will have a positive sign because the base is negative and the exponent is even
Perform the following operations with powers:
1
2
3 
4
5
6
7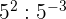
8
9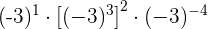
10
1
To multiply powers with the same base we keep the same base and add the exponents 
The result will have a positive sign because the base is negative and the exponent is even
2
First we decompose 27 into factors and then multiply powers with the same base 
The result will have a positive sign because the base is negative and the exponent is even
3
To multiply powers with the same base we keep the same base and add the exponents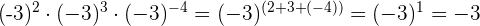 
The result will have a negative sign because the base is negative and the exponent is odd
4
To multiply powers with the same base we keep the same base and add the exponents 
Since the exponent is negative, we have to take the reciprocal of the base with positive exponent and then develop 
5
To divide powers with the same base we keep the same base and subtract the exponents 
Since the exponent is negative, we have to take the reciprocal of the base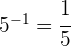 
6
To divide powers with the same base we keep the same base and subtract the exponents 
Since the exponent is negative, we have to take the reciprocal of the base with positive exponent and develop
7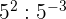
To divide powers with the same base we keep the same base and subtract the exponents 
8
To divide powers with the same base we keep the same base and subtract the exponents 
9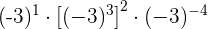
To raise a power to a power we keep the same base and multiply the exponents 
To divide powers with the same base we keep the same base and subtract the exponents 
The result will have a negative sign because the base is negative and the exponent is odd
10
We solve the brackets so to divide powers with the same base we keep the same base and subtract the exponents 
To raise a power to a power we keep the same base and multiply the exponents 
The result will have a negative sign because the base is negative and the exponent is odd
Perform the following operations with powers:
1
2
3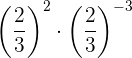
4
5
6
7
8
9
10
11
12
13
1
Since we are multiplying powers with the same base, we keep the base and add the exponents
2
Since we are multiplying powers with the same base, we keep the base and add the exponents
Since the resulting power has exponent one, then the power equals the base
3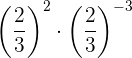
Since we are multiplying powers with the same base, we keep the base and add the exponents
Since the resulting power has a negative exponent, then the power equals the reciprocal of the base with positive exponent. Finally, the resulting power has exponent one, so the power equals the new base
4
Since we are multiplying powers with the same base, we keep the base and add the exponents
Since the resulting power has a negative exponent, then the power equals the reciprocal of the base with positive exponent.
5
We change the second element to positive exponent, for this the base changes to its reciprocal and we solve the multiplication of powers with the same base
The resulting power has exponent one, so the power equals the base
6
Since we are dividing powers with the same base, we keep the base and subtract the exponents
Since the resulting power has a negative exponent, then the power equals the reciprocal of the base with positive exponent. Finally, since the resulting power has exponent one, then the power equals the new base
7
Since we are dividing powers with the same base, we keep the base and subtract the exponents
Since the resulting power has a negative exponent, then the power equals the reciprocal of the base with positive exponent.
8
Since we are dividing powers with the same base, we keep the base and subtract the exponents
9
Since we are dividing powers with the same base, we keep the base and subtract the exponents
Since the resulting power has exponent one, then the power equals the new base
10
We change the first element to positive exponent, for this the base changes to its reciprocal and we solve the division of powers with the same base
11
Since this is a power of a power, we keep the base and multiply the exponents
12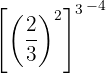 
Since this is a power of a power, we keep the base and multiply the exponents
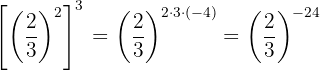
Since the resulting power has a negative exponent, then the power equals the reciprocal of the base with positive exponent.
13
We express the bases of the powers as powers of prime numbers
We change the first element to positive exponent, for this the base changes to its reciprocal and we solve the division of powers with the same base
Simplify the following expression:
1 We put all fractions with the same numerator and denominator, for this we decompose into factors the numbers that are not prime
2 We have elements that are powers of powers, so we keep the base and multiply the exponents
3 For the powers with base 
and negative exponents, we put the inverse fraction with positive exponent
4 Both in the numerator and denominator we multiply the powers with the same base and divide the results. Finally, we put the inverse fraction with a positive exponent
Simplify the following expression:
1 We first perform the multiplications and divisions inside the parentheses
2 We simplify those fractions where it is possible to do so, rewrite the mixed fractions and then calculate the sum in the parentheses
3 We rewrite the last expression and apply the properties of powers of rational numbers
4 We perform the divisions and simplify. Finally we perform the subtraction of the resulting fractions
Calculate the values of the following powers:
1 
2 
3 
4 
1
A power with a fractional exponent equals a root whose index is the denominator of the fraction and the exponent of the radicand is the numerator. We decompose 
into factors, perform the operations in the radicand and extract factors
2
We decompose 
into factors, perform the operations in the radicand and extract factors
3
In this case we convert the exponent which is an exact decimal number to a fraction, perform the operations in the radicand and extract factors
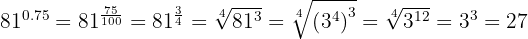
4 
We convert the exponent which is a pure repeating decimal to a fraction.
We substitute, perform the operations in the radicand and extract factors
How about a personalized review with a private math tutor?
Did you like this article? Rate it!
Loading...
