Chapters
Systems of equations with two variables are a fundamental tool in mathematics, used in various areas such as economics, physics, and engineering. These systems consist of two linear equations that must be solved simultaneously to find the value of the two unknowns. Solving a 2x2 system of equations allows us to determine intersection points on a Cartesian plane, providing solutions that can be unique, infinite, or nonexistent.

Solution by Substitution and Graphical Method
Solve the following system using the substitution method

The substitution method involves isolating one of the two variables from one equation and substituting it into the other. We will isolate  from the second equation:
from the second equation:

Note that we chose the second equation since it equals 0; this makes the procedure slightly simpler. Now we substitute the value of  into the first equation
into the first equation

Therefore,  . Then, we substitute the value of
. Then, we substitute the value of  into the expression we have for
into the expression we have for  :
:

Therefore, the solution is  .
.
Solve the following system using the substitution method

An advantage of the substitution method is that it is not necessary to simplify the system of equations to start solving. Therefore, we can start solving immediately.
First, we isolate  from the second equation:
from the second equation:
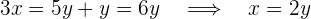
Then, we substitute the value of  into the first equation:
into the first equation:

From here, it follows that  . Now, we substitute the value of
. Now, we substitute the value of  into the expression we had for
into the expression we had for  :
:

Therefore, the solution to the system is  and
and  .
.
Solve the following system using the substitution method

First we isolate  from the second equation
from the second equation

Then, we substitute the value of  into the first equation:
into the first equation:

Therefore, the first equation becomes (by moving constants to the right side and variables to the left side)

which, by isolating  , we obtain
, we obtain

Then, substituting the value of  into the expression we have for
into the expression we have for  , we obtain
, we obtain

Therefore, the solution is  and
and 
Solve the following system using the substitution method

To solve this system, we must first eliminate the fractions (clear the denominators). To do this, we multiply the equations by the least common multiple of the denominators. For the first equation we have:

so  . While for the second equation we have:
. While for the second equation we have:

from which we obtain  . Thus, the system of equations becomes:
. Thus, the system of equations becomes:
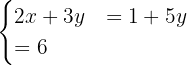
First we isolate  from the second equation:
from the second equation:

Then, we substitute the value of  into the first equation:
into the first equation:

so that  or
or  . Then, we substitute the value of
. Then, we substitute the value of  into the expression we had for
into the expression we had for  :
:

Therefore, the solution is  and
and  .
.
Solve the following system using the graphical method

The graphical method involves only graphing the two lines. The intersection will be the solution of the system:
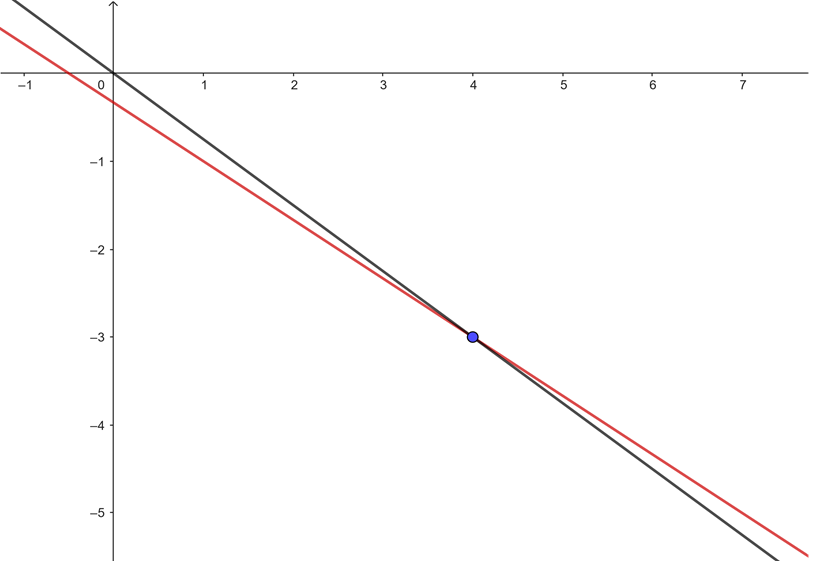
From the graph above we can observe that the solution is  and
and  . However, let's remember that we must be very precise when graphing.
. However, let's remember that we must be very precise when graphing.
Solution by Equalization
Let's recall that the equalization method can only be used to solve a system of 2 equations with 2 variables. Only this method and the graphical method are limited to  systems.
systems.

To solve the system by equalization we must isolate a variable from both equations. We isolate  from both equations:
from both equations:

from which we obtain  .
.
For the second equation we have

therefore  and
and  .
.
Now, we equate both equations

From that equation we isolate  :
:

so  . Then, we substitute the value of
. Then, we substitute the value of  into the first equation
into the first equation

so  . Therefore, the solution is
. Therefore, the solution is  and
and  .
.

As in the previous case, to solve by equalization we must isolate some variable from both equations. In this case we will isolate  . In the first equation we obtain:
. In the first equation we obtain:

While for the second equation we obtain:

Equating the equations, we have

so

so  . Then, substituting
. Then, substituting  into the first equation, we have
into the first equation, we have

so  . Thus, the solution is
. Thus, the solution is  and
and  .
.

As in the previous case, to solve by equalization we must isolate some variable from both equations. In this case we will isolate  . In the first equation we obtain:
. In the first equation we obtain:
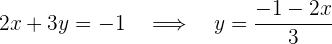
While for the second equation we obtain:

Equating the equations, we have

so

so  . Then, substituting
. Then, substituting  into the second equation, we have
into the second equation, we have  so
so  .
.
Thus, the solution is  and
and  .
.

Before applying the equalization method, we must write the system in a way that allows us to isolate one of the variables. To do this, we multiply both equations by 2:
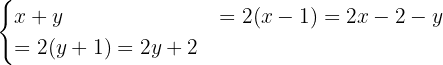
We isolate the variable y in both equations:
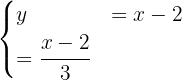
Equating the equations, we have

so

so  . Then, substituting
. Then, substituting  into the first equation, we have
into the first equation, we have  so
so  .
.
Thus, the solution is  and
and  .
.

First we isolate  from both equations
from both equations


Equating the equations, we have

so

so  . Then, substituting
. Then, substituting  into the second equation, we have
into the second equation, we have
 so
so  .
.
Thus, the solution is  and
and  .
.
Solution by Elimination
Let's recall that in the elimination method we must eliminate the  from all equations, except the first. Then we must eliminate the
from all equations, except the first. Then we must eliminate the  from all equations, except the first and second equation.
from all equations, except the first and second equation.
This method is the same as Gaussian elimination, with the only difference that we don't use the matrix associated with the system.

We need to eliminate the  from the second equation. To do this, we multiply the first equation by
from the second equation. To do this, we multiply the first equation by  and then subtract the result from the second equation:
and then subtract the result from the second equation:

Now, from the second equation we subtract the previous equation:
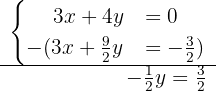
From here it follows that  . Then, we substitute the value of
. Then, we substitute the value of  into the first equation:
into the first equation:

Therefore  .
.

Before applying the elimination method, we must write the system so that the independent terms are on the right side. To do this, we multiply both equations by 2:
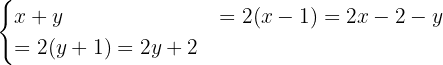
Then, we move the variables to the left side of the equations:
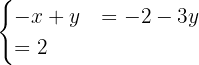
Now, to the second equation we add the first:
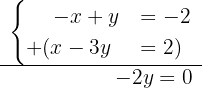
From here it follows that  . Then, we substitute the value of
. Then, we substitute the value of  into the first equation:
into the first equation:

Therefore, the solution is  and
and  .
.

We multiply the first equation by  and the second by 2
and the second by 2

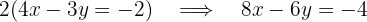
Now, we add both equations
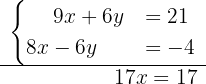
From here it follows that  . Then, we substitute the value of
. Then, we substitute the value of  into the first equation:
into the first equation:

Therefore  .
.

Before applying the elimination method, we must write the system so that the independent terms are on the right side. To do this, we multiply the first equation by 4 and isolate
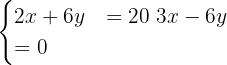
Now, to the second equation we add the first:

From here it follows that  . Then, we substitute the value of
. Then, we substitute the value of  into the second equation:
into the second equation:

Therefore, the solution is  and
and  .
.

Before applying the elimination method, we must write the system so that the independent terms are on the right side. To do this, we multiply both equations by 6 and 9 respectively
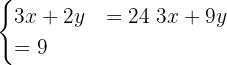
Now, from the first equation we subtract the second:
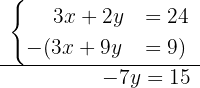
From here it follows that  . Then, we substitute the value of
. Then, we substitute the value of  into the second equation:
into the second equation:

Therefore, the solution is  and
and  .
.












