Inequalities are mathematical expressions that establish a relationship of inequality between two quantities. Unlike equations, which seek to equate two expressions, inequalities allow us to represent a range of values that satisfy certain conditions. These are widely used in various disciplines, such as economics, physics, and statistics, to model real situations where quantities are not fixed.
In these exercises it will be assumed that you already have knowledge about the definition of inequalities and some of their properties.
We will solve each of the exercises step by step. We must note that solving an inequality is practically the same as solving an equation, except that now we must pay close attention to the properties of inequalities, when they "change direction," etc. We will perform each algebraic step, trying to be as detailed as possible.
Find the solution of each of the following inequalities, or systems of inequalities, and graph their solution set.
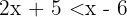
Let's proceed to solve the inequality. Remember that it is very similar to solving an equation, except that now instead of finding only one value for our variable, we find an entire domain, often formed by an interval or by unions or intersections of intervals. Our inequality is

Notice that this tells us that  , or equivalently, we have that its solution set is the interval
, or equivalently, we have that its solution set is the interval  .
.

Let's proceed. For this we will first use the distributive property and then solve for 

Notice that this tells us that  , or equivalently, we have that its solution set is the interval
, or equivalently, we have that its solution set is the interval  .
.


Let's proceed. For this we will get rid of the fractions first and then solve for  . To get rid of the fractions we need the least common multiple of the denominators, which is
. To get rid of the fractions we need the least common multiple of the denominators, which is 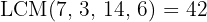 , thus, we obtain
, thus, we obtain

Notice that this tells us that  , or equivalently, we have that its solution set is the interval
, or equivalently, we have that its solution set is the interval  .
.

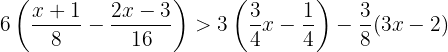
Let's proceed. For this, as in the previous exercises, we need to apply the distributive law and, in addition, eliminate the fractions

Notice that this tells us that:  , or equivalently, we have that its solution set is the interval
, or equivalently, we have that its solution set is the interval  .
.

To solve this system we must solve the inequalities separately and then find the values for which  satisfies both inequalities.
satisfies both inequalities.
Let's start with the first inequality

thus, from the first inequality we have that  , or equivalently, that
, or equivalently, that  belongs to the interval
belongs to the interval  . Now let's solve the second inequality
. Now let's solve the second inequality

thus, from the second inequality we have that  , or equivalently, that
, or equivalently, that  belongs to the interval
belongs to the interval  . Notice that x must satisfy both conditions, that is,
. Notice that x must satisfy both conditions, that is,  and
and  , this is equivalent to saying that
, this is equivalent to saying that  is in the intersection of the intervals
is in the intersection of the intervals  and
and  , thus, the solution set is
, thus, the solution set is



Let's proceed to solve the exercise

Notice that this tells us that  , however, the product is negative only when the expressions being multiplied have opposite signs, that is, we have two main cases, one is that
, however, the product is negative only when the expressions being multiplied have opposite signs, that is, we have two main cases, one is that 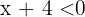 and
and  , or the other case is that
, or the other case is that 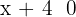 and
and  .
.
Let's evaluate each case, starting with the first one we mentioned. Suppose that 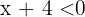 , then
, then  , also, we have that
, also, we have that 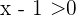 , then
, then 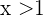 , that is
, that is  must satisfy that
must satisfy that  and
and 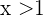 , or equivalently, it must belong to the intersection of the intervals
, or equivalently, it must belong to the intersection of the intervals  and
and  . Notice that the intersection is empty, these intervals do not intersect, therefore, from this case we obtain no solution.
. Notice that the intersection is empty, these intervals do not intersect, therefore, from this case we obtain no solution.
Now let's proceed with the second case, suppose that 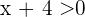 , then
, then 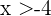 , also, we have that
, also, we have that  , then
, then  , this tells us that
, this tells us that  must satisfy that
must satisfy that 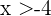 and
and  , or equivalently, it must belong to the intersection of the intervals
, or equivalently, it must belong to the intersection of the intervals  and
and  . Notice that the intersection is
. Notice that the intersection is  , this interval is the solution we seek.
, this interval is the solution we seek.


Let's proceed to solve the exercise

Notice that to express  as a product of first-degree expressions we must find its roots. For this, using the quadratic formula we have
as a product of first-degree expressions we must find its roots. For this, using the quadratic formula we have

however, notice that we have the square root of a negative number, therefore the roots of the polynomial are both complex numbers. That said, since we cannot write the polynomial as a product of real first-degree expressions, to find a solution we will substitute  with any real number we choose. If the inequality holds, then we will have that the solution is the set of real numbers
with any real number we choose. If the inequality holds, then we will have that the solution is the set of real numbers  . If it does not hold, then we will have that there is no solution. Let's substitute
. If it does not hold, then we will have that there is no solution. Let's substitute  , thus
, thus

Since it is true that 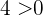 , then the solution set is
, then the solution set is  .
.

Let's solve

Notice that at the end we divided by  . Since the expression is strictly positive, it is impossible that
. Since the expression is strictly positive, it is impossible that  , therefore
, therefore  . Now, calculating the roots of
. Now, calculating the roots of 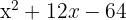 we can write our inequality as
we can write our inequality as

This tells us that 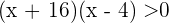 , however, the product is positive only when the expressions being multiplied have the same sign, that is, we have two main cases, one is that
, however, the product is positive only when the expressions being multiplied have the same sign, that is, we have two main cases, one is that  and
and  , or the other case is that
, or the other case is that 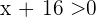 and
and 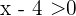 .
.
Let's evaluate each case, starting with the first one we mentioned. Suppose that  , then
, then  , also, we have that
, also, we have that  , then
, then  , that is
, that is  must satisfy that
must satisfy that  and
and  , or equivalently, it must belong to the intersection of the intervals
, or equivalently, it must belong to the intersection of the intervals  and
and  . Notice that the intersection is
. Notice that the intersection is  , therefore this is one solution.
, therefore this is one solution.
Now let's proceed with the second case, suppose that 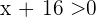 , then
, then 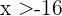 , also, we have that
, also, we have that 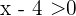 , then
, then 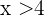 , this tells us that
, this tells us that  must satisfy that
must satisfy that 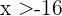 and
and 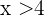 , or equivalently, it must belong to the intersection of the intervals
, or equivalently, it must belong to the intersection of the intervals  and
and  . Notice that the intersection is
. Notice that the intersection is  , this interval is also a solution.
, this interval is also a solution.
Thus, our final solution is the union of the two individual solutions we found, that is, the final solution is  .
.


Let's solve the exercise

This tells us that  , however, the product is negative only when the expressions being multiplied have opposite signs, that is, we have two main cases, one is that
, however, the product is negative only when the expressions being multiplied have opposite signs, that is, we have two main cases, one is that 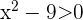 and
and  , or the other case is that
, or the other case is that  and
and 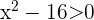 .
.
Let's evaluate each case, starting with the first one we mentioned. Suppose that 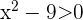 . First, we must again express this second-order polynomial as a product of first-degree expressions, that is
. First, we must again express this second-order polynomial as a product of first-degree expressions, that is

For this to be positive it must also be satisfied that  and
and  are of the same sign, that is, both positive or both negative. Assuming both are negative, we have that
are of the same sign, that is, both positive or both negative. Assuming both are negative, we have that 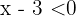 , then
, then  and
and  , then
, then  , this is equivalent to saying that
, this is equivalent to saying that  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Now suppose that  and
and  are positive, we have that
are positive, we have that 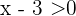 , then
, then 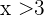 and
and 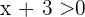 , then
, then 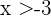 , this is equivalent to saying that
, this is equivalent to saying that  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Thus, for 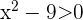 to hold,
to hold,  must belong to the union of the two intervals we found previously, that is,
must belong to the union of the two intervals we found previously, that is,  belongs to
belongs to  .
.
Since the assumption is that 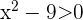 , we also have that
, we also have that  . We must express this second-order polynomial as a product of first-degree expressions, that is
. We must express this second-order polynomial as a product of first-degree expressions, that is

For this to be negative it must also be satisfied that  and
and  have opposite signs. Assuming that
have opposite signs. Assuming that  and
and 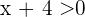 we have that
we have that  and
and 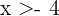 respectively, that is,
respectively, that is,  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Now suppose that 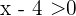 and
and 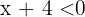 we have that
we have that 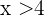 and
and  respectively, that is,
respectively, that is,  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is empty. Thus, the only way for
which is empty. Thus, the only way for  is that
is that  belongs to the interval
belongs to the interval 
All of the above tells us that for 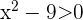 and
and  to hold,
to hold,  must belong to the intersection of the sets we found,
must belong to the intersection of the sets we found,  and
and  , which is
, which is  .
.
Let's proceed with our second main assumption, which is that  and
and 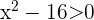 . Suppose that
. Suppose that  . First, we must again express this second-order polynomial as a product of first-degree expressions, that is
. First, we must again express this second-order polynomial as a product of first-degree expressions, that is

For this to be negative it must also be satisfied that  and
and  have opposite signs. Assuming that
have opposite signs. Assuming that 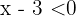 and
and 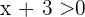 we have that
we have that  and
and 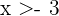 respectively, that is,
respectively, that is,  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Now suppose that 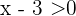 and
and  we have that
we have that 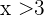 and
and  respectively, that is,
respectively, that is,  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is empty. Thus, the only way for
which is empty. Thus, the only way for  is that
is that  belongs to the interval
belongs to the interval 
We also have that 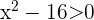 . We must express this second-order polynomial as a product of first-degree expressions, that is
. We must express this second-order polynomial as a product of first-degree expressions, that is

For this to be positive it must also be satisfied that  and
and  are of the same sign, that is, both positive or both negative. Assuming both are negative, we have that
are of the same sign, that is, both positive or both negative. Assuming both are negative, we have that  , then
, then  and
and 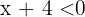 , then
, then  , this is equivalent to saying that
, this is equivalent to saying that  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Now suppose that  and
and  are positive, we have that
are positive, we have that 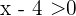 , then
, then 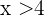 and
and 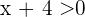 , then
, then 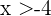 , this is equivalent to saying that
, this is equivalent to saying that  belongs to the intersection of the intervals
belongs to the intersection of the intervals  and
and  which is
which is  .
.
Thus, for  to hold,
to hold,  must belong to the union of the two intervals we found previously, that is,
must belong to the union of the two intervals we found previously, that is,  belongs to
belongs to  .
.
Therefore we have that for  and
and  to hold,
to hold,  must belong to the intersection of the sets we found,
must belong to the intersection of the sets we found,  and
and  , which is empty.
, which is empty.
Our final solution would be the union of the two solutions for each case. However, since the last solution is the empty set, our final solution is the set  .
.


Notice that

For the fraction to equal zero, the numerator must equal zero, that is  , therefore
, therefore  .
.
We have that for the fraction to be strictly negative, the numerator and denominator must have opposite signs. First suppose that the numerator is positive and the denominator negative, therefore 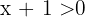 , that is
, that is 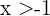 and
and  , therefore
, therefore  , this means that
, this means that  must belong to the intersection of the intervals
must belong to the intersection of the intervals  and
and  , which is
, which is  .
.
Now suppose that the numerator is negative and the denominator positive, therefore  , that is
, that is  and
and 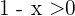 , therefore
, therefore 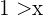 , this means that
, this means that  must belong to the intersection of the intervals
must belong to the intersection of the intervals  and
and  , which is
, which is  .
.
All of this tells us that for  to hold,
to hold,  must belong to the union of the two intervals we obtained and the point
must belong to the union of the two intervals we obtained and the point  , therefore, the solution set is
, therefore, the solution set is 

Summarize with AI:


