Welcome to our page of solved integral exercises! If you are a student, you should know that integral calculus is one of the most important areas of mathematics with countless applications in other areas of knowledge.
In this article, you will find step-by-step explanations, solved examples, and useful tips for solving integrals effectively using different integration techniques. Whether you are looking to improve your mathematical skills or simply need help with a specific problem, you've come to the right place!
We invite you to solve the following integrals yourself, and then check your answers with the collapsible solutions that Superprof has for you. Let's go!
Solve the following integrals
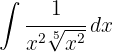
To solve the integral, we move the denominator up and simplify the powers, then apply the immediate power integral.
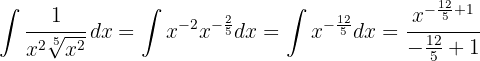
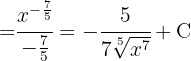
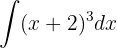
To solve the integral, we make the variable substitution  and then apply the immediate power integral.
and then apply the immediate power integral.


To solve the integral, we make the variable substitution 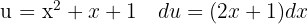 and then apply the immediate power integral.
and then apply the immediate power integral.
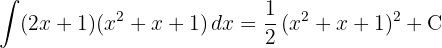

To solve the integral, we make the variable substitution 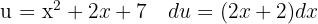 and then apply the immediate power integral.
and then apply the immediate power integral.

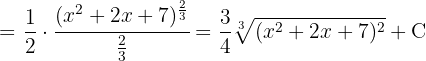
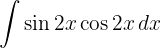
To solve the integral, we make the variable substitution  and then apply the immediate power integral.
and then apply the immediate power integral.
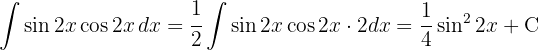
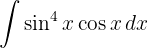
To solve the integral, we make the variable substitution  and then apply the immediate power integral.
and then apply the immediate power integral.
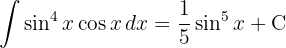
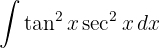
To solve the integral, we make the variable substitution 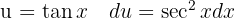 and then apply the immediate power integral.
and then apply the immediate power integral.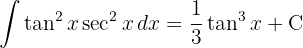
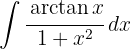
To solve the integral, we make the variable substitution 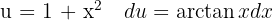 and then apply the immediate power integral.
and then apply the immediate power integral.
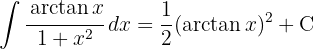
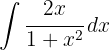
To solve the integral, we make the variable substitution  and then we apply the immediate integral
and then we apply the immediate integral 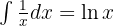 .
.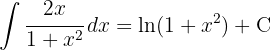
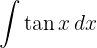
To solve the integral, we use the definition of tangent in terms of sine and cosine, then apply the immediate integral 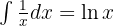 .
.

To solve the integral, we make the variable substitution  and then we apply the immediate integral
and then we apply the immediate integral 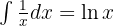 .
.
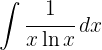
To solve the integral, we make the variable substitution 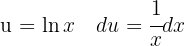 and then we apply the immediate integral
and then we apply the immediate integral 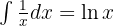 .
.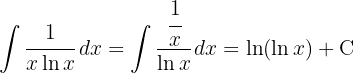

To solve the integral, we make the variable substitution  and then we apply the immediate integral
and then we apply the immediate integral 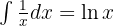 .
.
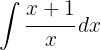
To solve the integral, we separate the integral and then apply the immediate integral 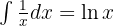 .
.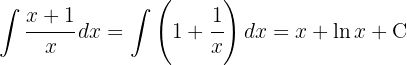
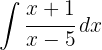
To solve the integral, we add a zero to be able to separate it into two integrals and then apply the immediate integral 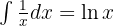 .
.

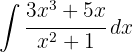
To solve the integral, we start by doing synthetic division to be able to separate it into two integrals and then apply the immediate integral 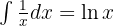 , with a variable substitution
, with a variable substitution  .
.
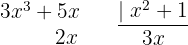
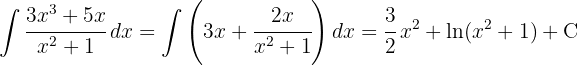
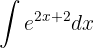
To solve the integral, we make the variable substitution  and then we apply the immediate integral
and then we apply the immediate integral  .
.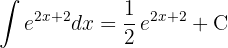

To solve the integral, we apply the immediate integral 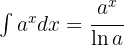 .
.
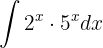
To solve the integral, we apply the immediate integral 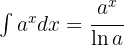 .
.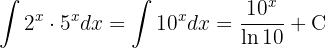
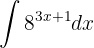
To solve the integral, we make the variable substitution 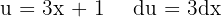 and then we apply the immediate integral
and then we apply the immediate integral 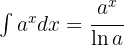 .
.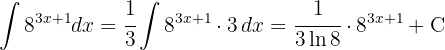
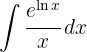
To solve the integral, we make the variable substitution 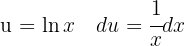 and then we apply the immediate integral
and then we apply the immediate integral  .
.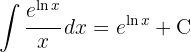

To solve the integral, we make the variable substitution  and then we apply the immediate integral
and then we apply the immediate integral  .
.

To solve the integral, we make the variable substitution 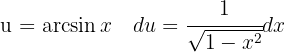 and then we apply the immediate integral
and then we apply the immediate integral  .
.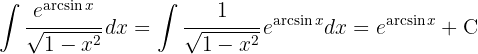
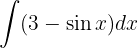
We start by separating the integral and applying the respective immediate integrals 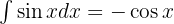


We start by making a variable substitution, 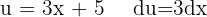 and applying the immediate integral
and applying the immediate integral 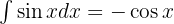 .
.

We start by making a variable substitution, 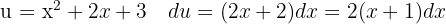 and applying the immediate integral
and applying the immediate integral 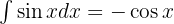 .
.
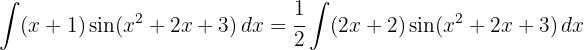

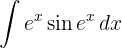
We start by making a variable substitution, 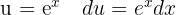 and applying the immediate integral
and applying the immediate integral 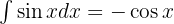 .
.

We start by making a variable substitution,  and applying the immediate integral
and applying the immediate integral 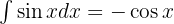 .
.

We start by using the identity 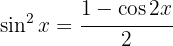 , separating the integral and applying the immediate integral
, separating the integral and applying the immediate integral  , with a variable substitution
, with a variable substitution 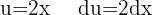 .
.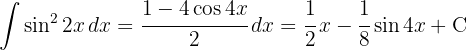
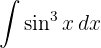
We start by separating the sine and using the trigonometric identity 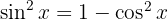 , applying the immediate integral
, applying the immediate integral 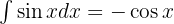 and a variable substitution
and a variable substitution 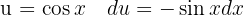
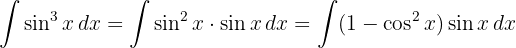
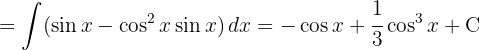
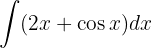
We start by separating the integral and applying the immediate integral 

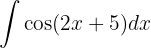
We start by making a variable substitution 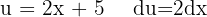 and applying the immediate integral
and applying the immediate integral 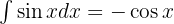
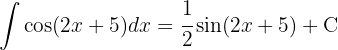
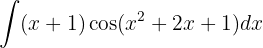
We start by making a variable substitution 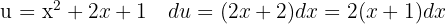 and applying the immediate integral
and applying the immediate integral 
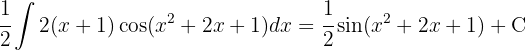

We start by making a variable substitution  and applying the immediate integral
and applying the immediate integral 


We start by using the trigonometric identity 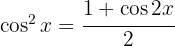 , separating the integral and applying the immediate integral
, separating the integral and applying the immediate integral  , with a variable substitution
, with a variable substitution 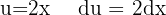

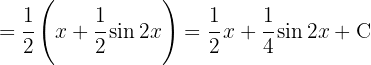

We start by using the trigonometric identity 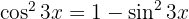 , separating the integral, applying the immediate integral
, separating the integral, applying the immediate integral  , and a variable substitution
, and a variable substitution 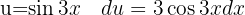


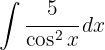
We start by using the trigonometric identity 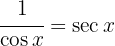 and applying the immediate integral
and applying the immediate integral 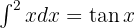 }
}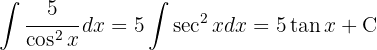

We start by using the trigonometric identity  and applying the immediate integral
and applying the immediate integral 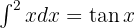 }
} 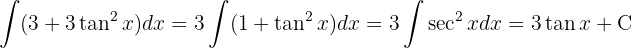

We start by making a variable substitution  and applying the immediate integral
and applying the immediate integral 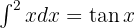 }
} 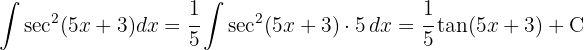

We start by separating the secant and using the trigonometric identity  , applying the immediate integral
, applying the immediate integral 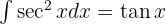 and a variable substitution
and a variable substitution 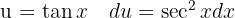
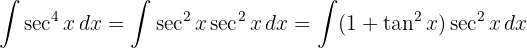

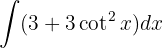
We start by using the trigonometric identity 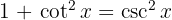 and applying the immediate integral
and applying the immediate integral 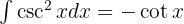
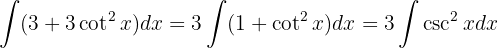
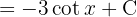

We start by adding a zero, using the trigonometric identity  , separating the integral and applying the immediate integral
, separating the integral and applying the immediate integral 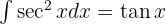

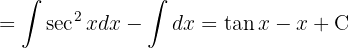
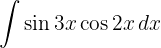
To solve the integral we are going to find the values of A and B that satisfy the following identity


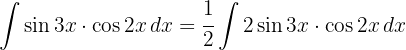
We apply the previous identity, a variable substitution 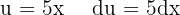 and apply the integral
and apply the integral 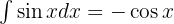
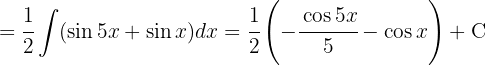
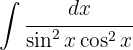
To solve the integral we use the trigonometric identity  , separate the integral and simplify,
, separate the integral and simplify,


Now we use the definitions 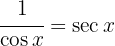 and
and 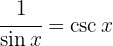 and finally the immediate integrals
and finally the immediate integrals  and
and 
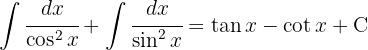
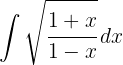
To solve the following integral we multiply the numerator and denominator by  , and then separate the integral
, and then separate the integral
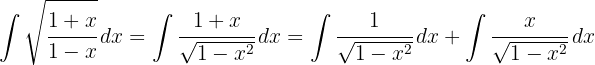
We apply the integral  and the variable substitution
and the variable substitution 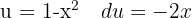
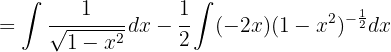


To solve the following integral we multiply the numerator and denominator by 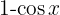 , expand the squared binomial, use the identity
, expand the squared binomial, use the identity 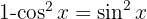 and then separate the integral
and then separate the integral
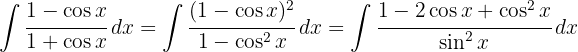
Now we use the definitions 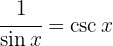 , the immediate integral
, the immediate integral  , a variable substitution
, a variable substitution 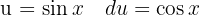 and add a zero, to be able to use the identity
and add a zero, to be able to use the identity 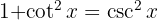 and finally the integral
and finally the integral 


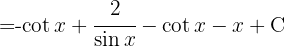

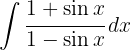
To solve the following integral we multiply the numerator and denominator by 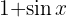 , expand the squared binomial, use the identity
, expand the squared binomial, use the identity 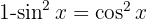 and then separate the integral
and then separate the integral
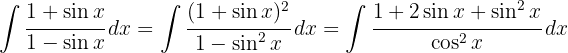

Now we use the definitions 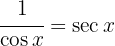 , the immediate integral
, the immediate integral 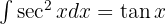 , a variable substitution
, a variable substitution 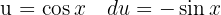 and add a zero, to be able to use the identity
and add a zero, to be able to use the identity 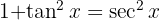
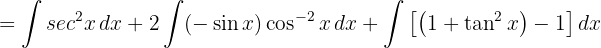
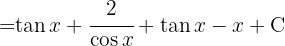
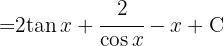

To solve the following integral we look to complete squares to have an integral of the form 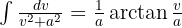 , where
, where 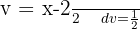 .
.
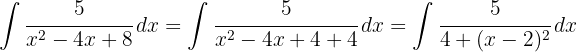
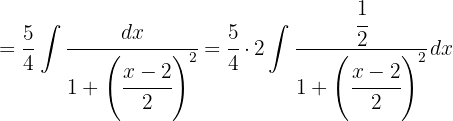
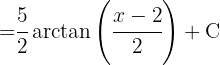

We start by separating the integral, on one hand we have a variable substitution  , on the other hand we look to have an integral of the form
, on the other hand we look to have an integral of the form 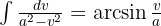 , where
, where  .
.
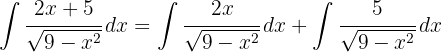
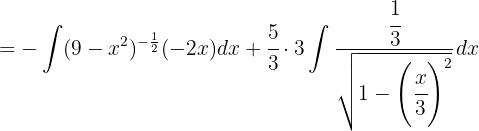


We look to have an integral of the form 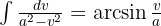 , where
, where  .
.
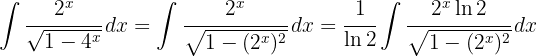
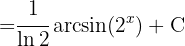
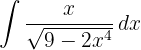
We look to have an integral of the form 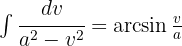 , so in the denominator we can make the following substitution:
, so in the denominator we can make the following substitution:

donde 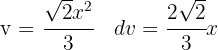 .
.



