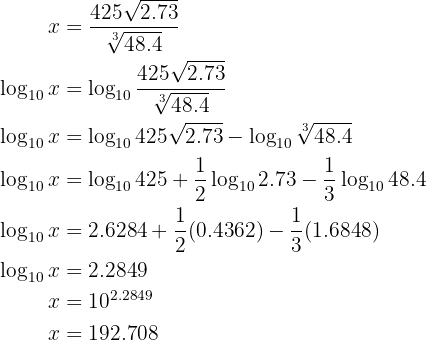To solve these exercises, let's remember the definition of a logarithm which tells us that if  is equal to the logarithm, base
is equal to the logarithm, base  , of
, of 

implies that  .
.
Now that we have that in mind, let's proceed to solve the exercises.

Logarithms by Definition
Applying the definition of logarithm, calculate the value of y
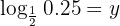
Our expression is

We apply the definition of logarithm and convert  to a fraction, that is
to a fraction, that is  , then simplify
, then simplify
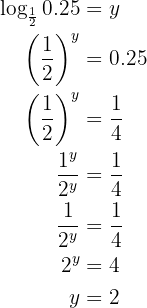
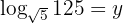
Our expression is
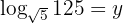
We apply the definition of logarithm
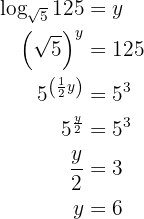
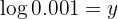
Our expression is
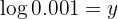
Note that when we write 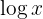 we refer to base
we refer to base  , that is
, that is 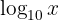
We apply the definition of logarithm
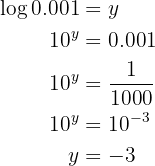
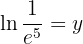
Our expression is
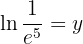
Remember that the natural logarithm is simply the logarithm base  , that is,
, that is, 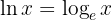 . We apply the definition of logarithm and solve
. We apply the definition of logarithm and solve
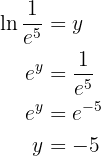
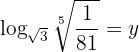
Our expression is
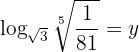
We apply the definition of logarithm and solve
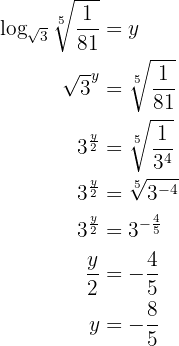
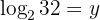
Our expression is
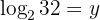
We apply the definition of logarithm and solve
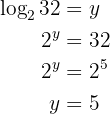
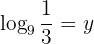
Our expression is
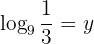
We apply the definition of logarithm and solve
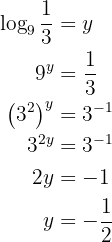

Our expression is

We apply the definition of logarithm and solve
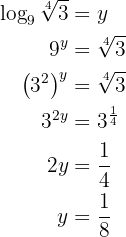

Our expression is

We apply the definition of logarithm and solve.
Note that in this case it is a bit different since  is the base of the logarithm.
is the base of the logarithm.
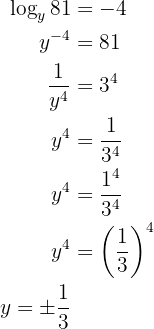
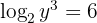
Our expression is
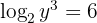
We apply the definition of logarithm and solve. Note that in this case it is a bit different since  is found in the argument of the logarithm.
is found in the argument of the logarithm.
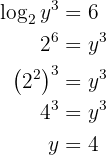
Logarithm Calculation
In these exercises we will apply the change of base property of logarithms, which tells us that the logarithm, base  , of
, of  is equal to
is equal to

for another base  . Note that the expression on the right is already in new base
. Note that the expression on the right is already in new base  .
.
Given 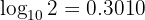 , calculate the following logarithm:
, calculate the following logarithm:
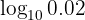
Our expression to solve is
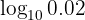
Let's proceed by converting the argument to an appropriate fraction
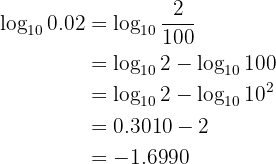
Given 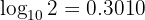 , calculate the following logarithm:
, calculate the following logarithm:

Our expression to solve is

We proceed by writing 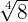 as a power of
as a power of  .
.
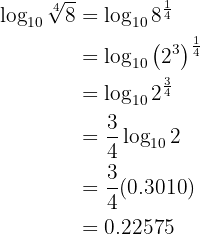
Given 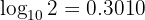 , calculate the following logarithm:
, calculate the following logarithm:
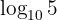
Our expression to solve is
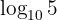
We proceed by writing  as
as  and then apply some properties of logarithms
and then apply some properties of logarithms
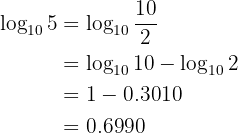
Given 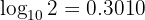 , calculate the following logarithm:
, calculate the following logarithm:
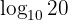
Our expression to solve is
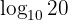
We proceed by writing  as
as 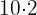 and then apply some properties of logarithms
and then apply some properties of logarithms
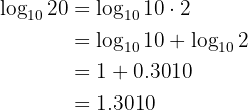
Given 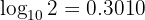 , calculate the following logarithm:
, calculate the following logarithm:
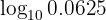
Our expression to solve is
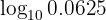
We proceed by writing 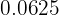 as a fraction in which there is a power of
as a fraction in which there is a power of  and apply properties of logarithms
and apply properties of logarithms
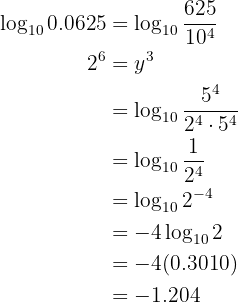
Given 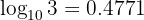 , calculate the following logarithm:
, calculate the following logarithm:
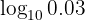
Our expression to solve is
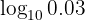
Let's proceed by converting the argument to an appropriate fraction
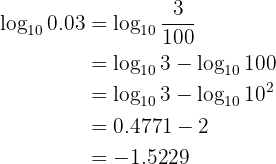
Given 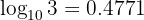 , calculate the following logarithm:
, calculate the following logarithm:
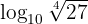
Our expression to solve is
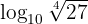
We proceed by writing 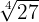 as a power of
as a power of  .
.
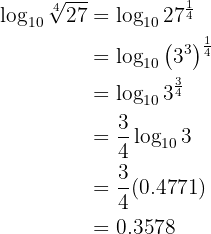
Given 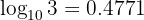 , calculate the following logarithm:
, calculate the following logarithm:
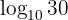
Our expression to solve is
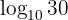
We proceed by writing  as
as 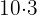 and then apply some properties of logarithms
and then apply some properties of logarithms
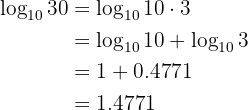
Given 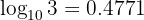 , calculate the following logarithm:
, calculate the following logarithm:
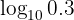
Our expression to solve is
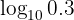
We proceed by writing 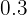 as a fraction in which there is a power of
as a fraction in which there is a power of  and apply properties of logarithms
and apply properties of logarithms
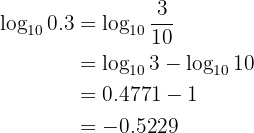
Given 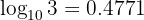 , calculate the following logarithm:
, calculate the following logarithm:
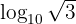
Our expression to solve is
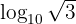
We proceed by writing 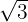 as a power of
as a power of  .
.
Logarithm Development
Develop the following expressions
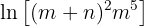
Here's how to solve the exercise:
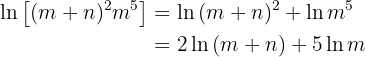
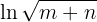
Here's how to solve the exercise:
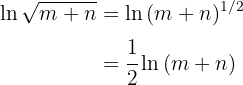
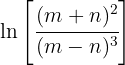
Here's how to solve the exercise:
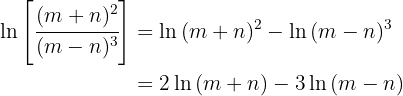
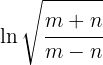
Here's how to solve the exercise:
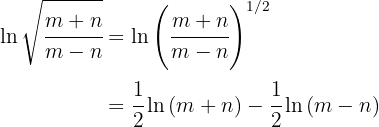
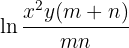
Here's how to solve the exercise:
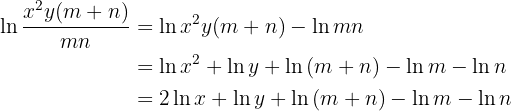

Here's how to solve the exercise:
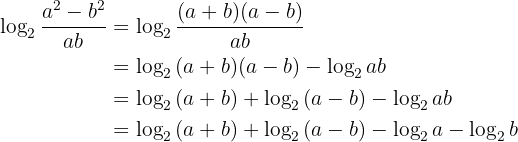

Here's how to solve the exercise:
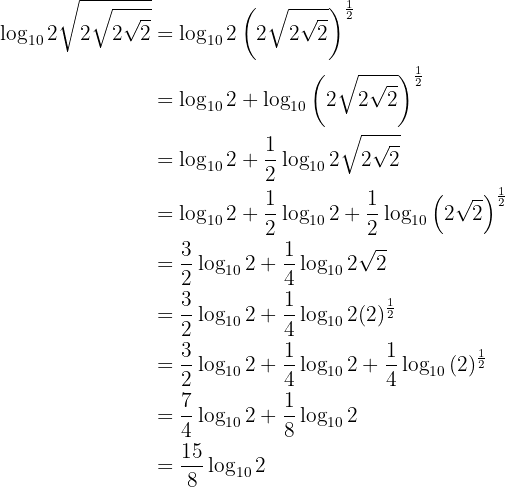
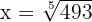
Here's how to solve the exercise:
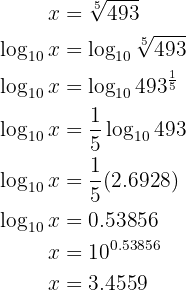

Here's how to solve the exercise:


Here's how to solve the exercise: