Find the equation of the line with slope 5 that passes through the point 
We use the point–slope form of a line:

If we substitute the known values, the equation of the line is:

Therefore, the equation of the line is:

Find the equation of the line with slope −3 that passes through the point (0,11)
We use the slope–intercept form of a line:

Substituting the known values, the equation of the line is:

Therefore, the equation of the line is:
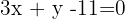
Find the equation of the line that passes through the points and 
We find the slope of the line:

We use the slope–intercept form of a line:

Substituting the known values, the equation of the line is:

Therefore, the equation of the line is:

Find the equation of the line that passes through  and is parallel to the line
and is parallel to the line 
We find the slope of the line 

Since the line that passes through  is parallel to the given line, both lines have the same slope
is parallel to the given line, both lines have the same slope 
We substitute the slope and the point into the point–slope equation:
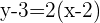
Therefore, the equation of the line is:

Find the equation of the line that passes through  and is perpendicular to the line
and is perpendicular to the line 
We find the slope of the line 

Since the line that passes through the point  is perpendicular to the line
is perpendicular to the line  , then its slope is
, then its slope is 
We substitute the slope and the point through which the line passes into the point-slope equation and obtain

Therefore, the equation of the line is:

Determine whether the lines  and
and  are parallel, perpendicular, or neither.
are parallel, perpendicular, or neither.
We find the slope of the line  .
.

We find the slope of the line  .
.

Since  , the lines are not parallel.
, the lines are not parallel.
Since  , the lines are not perpendicular.
, the lines are not perpendicular.
Therefore, the lines are neither parallel nor perpendicular.
Determine whether the lines  and
and  are parallel, perpendicular, or neither.
are parallel, perpendicular, or neither.
We find the slope of the line  .
.

We find the slope of the line  .
.

Since  , the lines are not parallel.
, the lines are not parallel.
Since 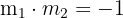 , the lines are perpendicular.
, the lines are perpendicular.
Determine whether the lines  and
and  are parallel, perpendicular, or neither.
are parallel, perpendicular, or neither.
We find the slope of the line  .
.

We find the slope of the line  .
.

Since  , the lines are parallel.
, the lines are parallel.
Write all possible forms of the equation of the line that passes through the points  and
and  .
.
We know that the line passes through the points  and
and  . Therefore, the vector that joins these two points is:
. Therefore, the vector that joins these two points is:

With this information we can obtain the equations of the line.
Equation of the line through two points:

Vector equation:

Parametric equations:

Continuous equation:

General equation:

Explicit equation:

Point-slope equation:

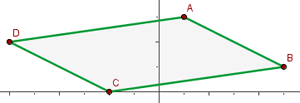
Given the parallelogram  with
with  , find the coordinates of vertex
, find the coordinates of vertex  .
.
Before finding the coordinates of the vertex, let us observe the following figure.
We know that the vector from  to
to  must be equal to the vector from
must be equal to the vector from  to
to  , that is:
, that is:

We perform the calculations:
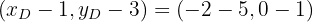
where  is the x-coordinate of point
is the x-coordinate of point  , and is its y-coordinate. Thus, we have:
, and is its y-coordinate. Thus, we have:

Therefore, point  is
is

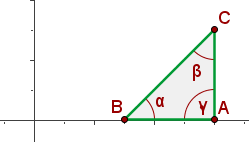
Classify the triangle determined by the points: 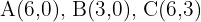 .
.
To classify the triangle, we must first calculate the length of each of its sides. We do this as follows:
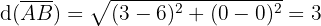
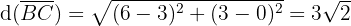
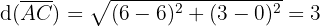
Let us note that the following holds:
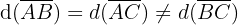
Therefore, the triangle is isosceles. In addition, the following also holds:
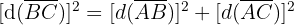
Thus, the triangle is also right-angled. This can be observed in the following figure.
Find the slope and the y-intercept of the line 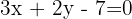 .
.
We solve for  :
:

From this, we can see that the slope is:
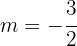
While the y-intercept is:

Study the relative position of the lines with equations:
a 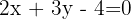
b 
c 
d 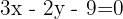
Let us note that the coefficients of line 1 and line 2 are proportional:

Therefore, lines 1 and 2 are coincident (they are the same line).
Likewise, let us note that the coefficients of  and
and  in lines 1 and 3 are proportional; however, the constant terms are not proportional:
in lines 1 and 3 are proportional; however, the constant terms are not proportional:

Therefore, lines 1 and 3 are parallel. Consequently, lines 2 and 3 are parallel (since lines 1 and 2 are the same).
Finally, let us observe that the coefficients of  and
and  in line 4 are not proportional to the coefficients of any other line:
in line 4 are not proportional to the coefficients of any other line:

Therefore, line 4 intersects lines 1, 2, and 3.
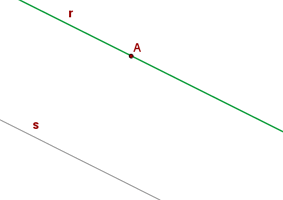
Find the equation of the line  that passes through
that passes through 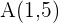 and is parallel to the line
and is parallel to the line  .
.
Let us observe the following figure of two parallel lines.
We know that two lines are parallel if they have the same slope:
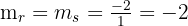
Therefore, line  has the following form (point–slope):
has the following form (point–slope):
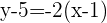
Setting the equation equal to zero, we obtain:

Given the quadrilateral  with vertices
with vertices 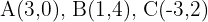 and
and 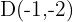 . Verify that it is a parallelogram and determine its center.
. Verify that it is a parallelogram and determine its center.
For the quadrilateral to be a parallelogram, we must have:
 and
and
Let us note that:
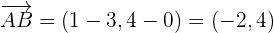
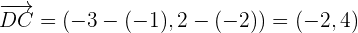
Therefore,  .
.
On the other hand:
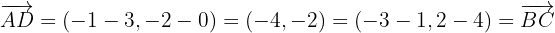
Thus, the quadrilateral is a parallelogram.
Now we must find the midpoint. We know that the diagonals intersect at their midpoint (which is the center of the parallelogram), so it is sufficient to find the midpoint of one diagonal. The midpoint of diagonal  is:
is:
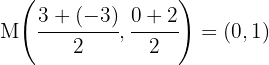
Thus, the center is point 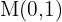 . Let us observe the figure of the parallelogram.
. Let us observe the figure of the parallelogram.
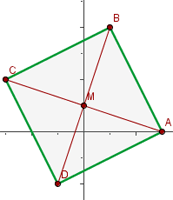
Find the equation of the line that passes through the point (2, -3) and is parallel to the line that joins the points (4, 1)and (-2, 2)
Let  be the line that joins the given points. Then the line
be the line that joins the given points. Then the line  we are looking for is parallel to
we are looking for is parallel to  . Therefore, they have the same slope:
. Therefore, they have the same slope:
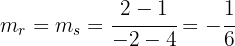
Using the point–slope form, the equation of line  is:
is:
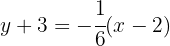
Therefore, the equation of  , written equal to zero, is:
, written equal to zero, is:
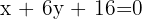
Points  and
and 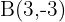 are vertices of an isosceles triangle
are vertices of an isosceles triangle  , whose vertex
, whose vertex  lies on the line
lies on the line 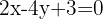 , with
, with  and
and 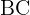 being the equal sides. Find the coordinates of vertex
being the equal sides. Find the coordinates of vertex  .
.
Let us write the coordinates of point  as
as 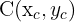 . Since
. Since 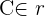 , we have:
, we have:
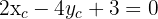
Solving for  :
:
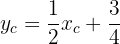
Additionally, since sides  and
and  are equal, we have:
are equal, we have:
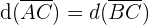
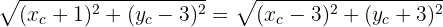
Squaring both sides:
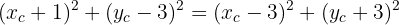
Substituting  :
:
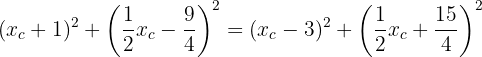
Expanding and solving the resulting equation (the quadratic terms cancel), we obtain:
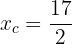
Substituting into the equation for  :
:
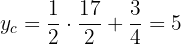
Therefore, the point is:
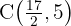
The line passes through point  and is parallel to line
and is parallel to line 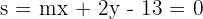 . Find
. Find  and
and  .
.
Since line  passes through point
passes through point  , substituting its coordinates gives:
, substituting its coordinates gives:
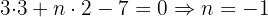
Since 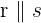 , the coefficients are proportional:
, the coefficients are proportional:
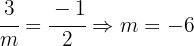
Therefore:

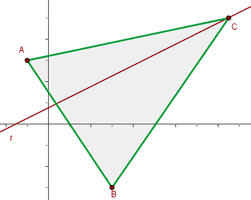
Given triangle  with coordinates
with coordinates 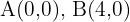 and
and  , find the equation of the median that passes through vertex
, find the equation of the median that passes through vertex  .
.
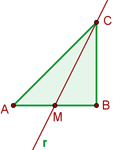
The median passes through the midpoint of segment  . We compute this point:
. We compute this point:
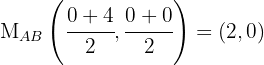
We now write the equation of the line that passes through points  and
and 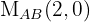 :
:
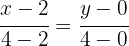
Simplifying, we obtain:
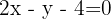
In a parallelogram, one vertex is known: 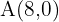 , and the intersection point of the diagonals is
, and the intersection point of the diagonals is 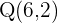 . Another vertex is at the origin. Find:
. Another vertex is at the origin. Find:
a The other vertices
b The equations of the diagonals
c The lengths of the diagonals
a) The other vertices
Since is the midpoint of segment  :
:

Thus:

So  .
.
Since is also the midpoint of segment  :
:

Thus:

In this way,  . Thus, the four vertices are the points
. Thus, the four vertices are the points  and
and  .
.
b The equations of the diagonals.
In this case we only have to use the formula for the line that passes through two points. First, for the diagonal  :
:

Simplifying a bit, we obtain  . Then, for the diagonal
. Then, for the diagonal  we have:
we have:

Which, after simplifying, we obtain 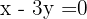 .
.
c The length of the diagonals.
To calculate the length of the diagonals, it is enough to calculate the distance between the appropriate vertices. For the diagonal  we have:
we have:

While for the diagonal  the length is:
the length is:
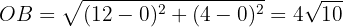
The graph of the parallelogram is the following:
Summarize with AI:


